【论文笔记】SIFA——基于GAN的双向跨模态无监督域适应框架

本文是论文《Unsupervised Bidirectional Cross-Modality Adaptation via Deeply Synergistic Image and Feature Alignment for Medical Image Segmentation》的阅读笔记。

文章提出了一个名为 SIFA（Synergistic Image and Feature Alignment）的无监督域适应框架。SIFA 的代码见 github。SIFA 从图像和特征两个角度引入了对齐的协同融合。

一、相关工作

域适应就是将从源域学习到的知识迁移到目标域中，在此之前 CycleGAN 在域适应方面取得了很好的效果。

SIFA 的一个关键特点是图像变换和分割任务的共享编码器。通过参数共享，本框架中的图像对齐和特征对齐能够协同工作，减少端到端训练过程中的域偏移（domain shift）。同时，另一个研究方向是特征对齐，目的是在对抗性学习的情况下提取深度神经网络的域不变特征。

二、记号

• $s$：源域
• $t$：目标域
• $G_t$：从源域到目标域的生成器，生成 $x^{s\to t}$
• $D_t$：从源域到目标域的判别器，判别图像是生成的还是真正来自目标域的
• $E$：特征编码器
• $U$：解码器
• $C$：像素级分类器
• $G_s=E\circ U$：特征编码器+解码器相当于一个源域生成器，生成 $x^{t\to s}$
• $E\circ C$：特征编码器+像素级分类器相当于一个分割网络，产生目标域图像和生成的目标域图像的分割标签
• $D_s$：判别生成的源域图像来自生成的目标域图像 $x^{s\to t}$ 还是来自真正的目标域图像 $x_t$ 的判别器
• $D_p$：对分割网络生成的分割标签进行判别的判别器
• ${\mathcal{L}}_{adv}^t(G_t,D_t)$：目标域 GAN（$G_t,D_t$）的目标函数
• ${\mathcal{L}}_{cyc}(G_t,E,U)$：源域-目标域-源域或目标域-源域-目标域的循环一致性损失
• ${\mathcal{L}}_{seg}(E,C)$：分割网络的混合损失
• ${\mathcal{L}}_{adv}^p(E,C,D_p)$：判别器 $D_p$ 的对抗损失
• ${\mathcal{L}}_{\text{adv }}^s(E,D_s)$：判别器 $D_s$ 的对抗损失
• ${\mathcal{L}}_{\text{adv }}^{\tilde{s}}(E,D_s)$：判别器 $D_s$ 辅助任务的对抗损失

三、方法

1. 用于图像对齐的外观转变

由于域偏移，跨域之间的图片通常看起来不同，而图像对齐的目的就是减少源域图像和目标域图像之间的这种差异。即给定一个有标签的来自源域的数据集 $\{x_i^s,y_i^s{\}}_{i=1}^N$，以及一个无标签的来自目标域的数据集 $\{x_i^t{\}}_{j=1}^M$，使得源域图像 $x_i^s$ 尽可能的看起来像 目标域图像 $x_i^t$。转换后的图像不仅要看起来像来自目标域，而且还应该保留源域的结构语义内容。

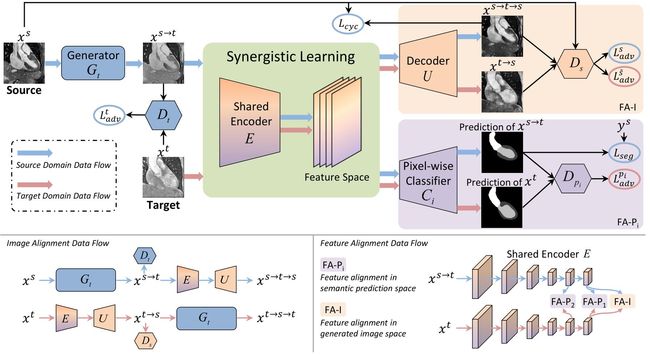
上图是网络的整体结构示意图，可结合以下描述来加以理解。

（1）外观转变

使用一个生成器 $G_t$ 将源域图像转换成与目标域相似的图像，即 $G_t(x^s)=x^{s\to t}$，并使用一个判别器 $D_t$ 来判断生成的图像是真正来自目标域还是生成的。这个 GAN 的目标函数为：
$$\begin{array}{rl}{\mathcal{L}}_{\text{adv}}^t\left(G_t,D_t\right)=& {\mathbb{E}}_{x^t\sim X^t}\left[\log D_t\left(x^t\right)\right]+\\ & {\mathbb{E}}_{x^s\sim X^s}\left[\log \left(1-D_t\left(G_t\left(x^s\right)\right)\right)\right]\end{array}$$
为了让转换得到的图像 $x^{s\to t}$ 保留源域的特征，通常使用一个反向的生成器来促进图像的循环一致性。图中的 E 是特征编码器，U 是解码器，E 和 U 加起来就相当于一个生成器 $G_s$，即 $G_s=E\circ U$ ，它可以将转换得到的目标域图像 $x^{s\to t}$ 再转换回源域。并通过源域的判别器 $D_s$ 进行判别，其对抗损失为 ${\mathcal{L}}_{adv}^s$，和目标域上的 GAN 的训练方式一致。通过源域-目标域-源域（$x^{s\to t\to s}=U\left(E\left(G_t\left(x^s\right)\right)\right)$）或目标域-源域-目标域（$x^{t\to s\to t}=G_t\left(U\left(E\left(x^t\right)\right)\right)$）的转换就得到了图像的循环一致性损失，即：
$$\begin{array}{rl}{\mathcal{L}}_{\mathrm{c}\mathrm{y}\mathrm{c}}\left(G_t,E,U\right)=& {\mathbb{E}}_{x^s\sim X^s}{\Vert U\left(E\left(G_t\left(x^s\right)\right)\right)-x^s\Vert }_1+\\ & {\mathbb{E}}_{x^t\sim X^t}{\Vert G_t\left(U\left(E\left(x^t\right)\right)\right)-x^t\Vert }_1\end{array}$$

（4）目标域的分割网络

图中的 C 是一个像素级的分类器，E 和 C 加起来 $E\circ C$ 就相当于一个目标域的分割网络，它的输入包括 $x^{s\to t},y^s,x^t$，输出是 $x^{s\to t},x^t$ 的分割标签，分割网络通过最小化一个混合损失（分割损失）来优化：
$${\mathcal{L}}_{seg}(E,C)=H(y^s,C\left(E\left(x^{s\to t}\right)\right)+\mathrm{Dice}\left(y^s,C\left(E\left(x^{s\to t}\right)\right)\right)$$
其中第一项是交叉熵，第二项是 Dice 损失。

2. 特征对齐的对抗学习

为解决跨域的域偏移问题，文章提出了另外的判别器来从特征对齐的角度来减少生成的目标图像 $x^{s\to t}$ 和真正的目标图像 $x^t$ 的 domain gap。为了对齐以上两种图像的特征，通常的方法是在特征空间直接使用对抗学习，但是特征空间一般是高维的，很难直接对齐。所以文章使用的方法是在两个低维的空间内使用对抗学习，一个是语义预测空间，另一个是生成图像空间。

（1）在语义预测空间的特征对齐

使用判别器 $D_p$ 来对分割网络生成的分割标签进行判别，如果两者的特征没有对齐的话，就通过反向传播对特征提取器 E 进行优化，从而减小生成的目标域图像 $x^{s\to t}$ 和真正的目标域图像 $x^t$ 的特征分布之间的差异。该对抗损失为：
$$\begin{array}{rl}{\mathcal{L}}_{adv}^p\left(E,C,D_p\right)=& {\mathbb{E}}_{x^{s\to t}\sim X^{s\to t}\left[\log D_p\left(C\left(E\left(x^{s\to t}\right)\right)\right)\right]+}\\ & {\mathbb{E}}_{x^t\sim X^t\left[\log \left(1-D_p\left(C\left(E\left(x^t\right)\right)\right)\right)\right]}\end{array}$$

（2）语义预测空间的深度监督对抗学习

低级特征可能和高级特征的对齐情况并不一样，所以使用额外的和编码器低层的输出相关的像素级分类器来产生额外的辅助预测，然后通过一个判别器来对这些额外预测进行判别。这增强了低级特征的对齐，如此一来，${\mathcal{L}}_{seg}$ 和 ${\mathcal{L}}_{adv}$ 的表达式就需要进行调整了，它们分别被拓展为 ${\mathcal{L}}_{seg}^i(E,C_i)$ 和 ${\mathcal{L}}_{adv}^{P_i}(E,C_i,D_{p_i})$，其中 $i=1,2$，$C_1,C_2$ 表示连接到编码器不同层的两个分类器，$D_{p_1},D_{p_2}$ 表示对两个分类器的输出进行判别的判别器。

（4）生成图像空间的特征对齐

对于生成器 $E\circ U$，为判别器 $D_s$ 增加一个辅助任务——判别生成的源域图像来自生成的目标域图像 $x^{s\to t}$ 还是来自真正的目标域图像 $x^t$。该辅助任务的对抗损失为：
$$\begin{array}{rl}{\mathcal{L}}_{\text{adv }}^{\tilde{s}}\left(E,D_s\right)=& {\mathbb{E}}_{x^{s\to }t\sim X^{s\to t}}\left[\log D_s\left(U\left(E\left(x^{s\to t}\right)\right)\right)\right]+\\ & {\mathbb{E}}_{x^t\sim X^t}\left[\log \left(1-D_s\left(U\left(E\left(x^t\right)\right)\right)\right)\right]\end{array}$$

3. 用于协同学习的共享编码器

在协同学习框架的一个关键是在图像和特征对齐之间共享编码器 E，编码器 E 会通过损失 ${\mathcal{L}}_{adv}^s$ 和 ${\mathcal{L}}_{cyc}$，以及判别器 $D_{p_i},D_s$ 的反向传播来进行优化。

在训练时各个模块的训练顺序为：$G_t\to D_t\to E\to C_i\to U\to D_s\to D_{p_i}$。整个网络的目标函数为：
$$\begin{array}{rl}\mathcal{L}=& {\mathcal{L}}_{adv}^t\left(G_t,D_t\right)+{\lambda }_{adv}^s{\mathcal{L}}_{adv}^s\left(E,U,D_s\right)+\\ & {\lambda }_{\mathrm{g}\mathrm{s}}{\mathcal{L}}_{\mathrm{c}\mathrm{s}\mathrm{c}}\left(G_t,E,U\right)+{\lambda }_{\mathrm{seg}}^1{\mathcal{L}}_{\mathrm{seg}}^1\left(E,C_1\right)+\\ & {\lambda }_{\mathrm{seg}}^2{\mathcal{L}}_{\mathrm{seg}}^2\left(E,C_2\right)+{\lambda }_{adv}^{p_1}{\mathcal{L}}_{adv}^{p_1}\left(E,C,D_{p_1}\right)+\\ & {\lambda }_{\text{adv}}^{p_2}{\mathcal{L}}_{adv}^{p_2}\left(E,C,D_{p_2}\right)+{\lambda }_{adv}^{\tilde{s}}{\mathcal{L}}_{ab}^{\tilde{s}}\left(E,D_s\right)\end{array}$$
其中 $\left\{{\lambda }_{adv}^s,{\lambda }_{cyc},{\lambda }_{seg}^1,{\lambda }_{seg}^2,{\lambda }_{adv}^{p_1},{\lambda }_{adv}^{p_2},{\lambda }_{adv}^{\tilde{s}}\right\}$ 是用于平衡各项的参数，在实验时分别设为 $\{0.1,10,1.0,0.1,0.1,0.01,0.1\}$。

四、网络设置和实施细节

• 生成器 $G_t$ 采用的是和 CycleGAN 中一样的设置，包括3个卷积层，9个残差块，2个反卷积层，然后再通过一个卷积层获得生成的图像。
• 解码器 U 包括1个卷积层，4个残差块，3个反卷积层，然后再通过一个卷积层获得输出。
• 判别器 $\{D_t,D_s,D_p\}$ 采用的是和 PatchGAN 一样的设置，它的输入是 $70\times 70$ 的patches，它包括5个卷积层，除了最后两层卷积层步长为1，其他的卷积核为4，步长为2。特征图的个数分别为 $\{64,128,256,512,1\}$。在前四层卷积层中每个卷积层后都跟着一个实例正则化和一个0.2的 Leaky ReLU。
• 编码器 E 使用残差连接和空洞卷积（dilation rate=2），来扩大分辨率的大小。用 $\{Ck,Rk,Dk\}$ 分别表示通道数为 $k$ 的卷积层、残差块和空洞残差块；用 M 表示步长为 2 的最大池化层；则编码器的构成为 $\{C16,R16,M,R32,M,2\times R64,M,2\times R128,4\times R256,2\times R512,2\times D512,2\times C512\}$。每个卷积操作后都跟着一个批正则化和 ReLU 激活函数。
• 像素级分类器 $C_1$ 连接到编码器 E 的最后一层（$2\times C512$）后面来得到输出，$C_2$ 最后连接到编码器 E 的 $2\times R512$ 块的后面来得到输出。$C_1,C_2$ 都只包含一个 $1\times 1$ 的卷积层。
• batch size 为8，使用的是 Adam 优化器，学习率为 $2\times 10^{-4}$。