《机器学习-小知识点》4：SGD,momentum,RMSprop,AdaGrad ,Adam

《机器学习-小知识点》4：SGD,momentum,RMSprop,AdaGrad ,Adam

都是个人理解，可能有错误，请告知

---

4.1 知识点定位

我们简单说一下整个神经网络学习过程:

1. 我们数据是已知的，网络结构是已知的，目的就是找到该网络一套最佳的参数[w,b]
2. 最佳的参数[w,b] 是什么标准呢？就是在这组参数确定的神经网络中，所有数据通过该神经网络，得到的预测值与真实值差距计算总和的平均值最小（目标是0）
   • 不是一个数据预测对了就行，是所有数据都得参加
   • 要算平均最小，是因为排除数量不同的影响
   • 我们目的是每次都能预测对，也就是追求一套参数，让每次都不出错，没有误差
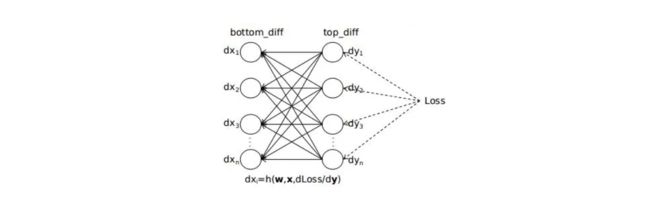
3. 调整[w,b]是在反向传播的过程中，方式是梯度下降。
4. 为了减少运算时间，有两种优化思路：对神经网络本身进行优化：dropout等；还有就是优化梯度下降。
5. SGD,momentum,RMSprop,Ddam都是梯度下降里的改进方法。

---

4.2 传统梯度下降

传统梯度下降比如三层参数，1000个数据，每层1000个参数（n=1000）

我们先通过1000个数据 算出了总损失函数，现在要反向传播，进行调整初始化的[w,b],【3层 -> 2层】反向传播一层为例：

第一个数据，通过反向传播，更新一次参数，不过这个更新暂存的，实际的参数没有变化。然后使用原始的参数更新一次第二个例子，然后使用原始参数更新一次第三个例子…这样一层参数更新了所有数据1000次，我们把这1000次计算出来需要的update的参数量求和或者求平均，从而更新一次参数。更新这一层参数的计算量1000*1000

它的问题是计算量太大了，尤其深度神经网络，无法实际应用。

---

4.3 SGD随机梯度下降法

想法：调查全国30岁人均身高，不需要把所有30岁人身高都计算出来，就随机抽样就行，无非是抽样数据越大，就约准确。即使抽取1个，那么离真是平均值相差不大。

用法：每次修改参数，随机取一个数据，下次再随机取一个，而不是用所有数据。

优势：相对于传统的梯度下降，大大降低了计算量，让理论方法得以实践

思考：在每轮更新中，难免会遇到误差很大的点，那么考虑 既不用1个数据，也不用所有数据，用一部分数据，这种就是mini-batch

• mini-batch:设置越大，那么梯度下降方向和最佳路线就更准确，但是计算量就越大。重要的是把我这个度.

缺点：

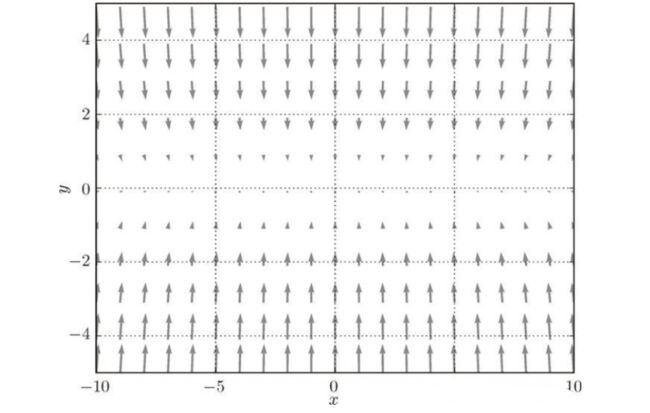
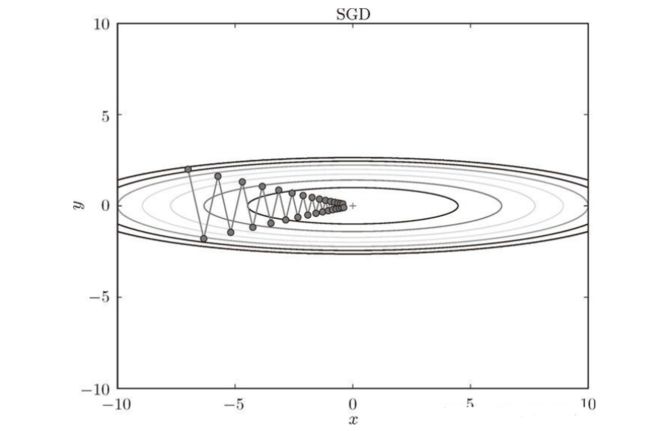
类似与这种收敛，会来回震荡，因为梯度下降方向很小的向量指向目标点（0.0）

---

4.4 momentum 动量法

思路：如SGD问题，会来回震荡，我们发现，我们目的是向前（红），在竖直方向上，来回反转（黄，绿），如果能够考虑历史原因，将上下方向有一定抵消，那么会减少震荡

公式：
$$V_t=\beta \cdot V_{t-1}+(1-\beta )\cdot d{w}_{(t)i}$$$$W_{(t)i}=W_{(t-1)i}+\eta V_t$$

• Vt其实就是W在t步的修正量，它参考了所有的历史数据，越近的影响的权重越大
• η是学习率
• $W_{(t)i}=\frac{\partial J(W_{(t-1)i})}{\partial W_i}$ ，就是w的梯度

第一个式子理解参看视频【16分钟时候开始】https://www.bilibili.com/video/BV1r64y1s7fU/

缺点：它的问题就是学习率η是一致不变的，可能会因为冲最佳点，反复震荡

---

4.5 AdaGrad 自适应算法

这个是想办法修改学习率η，让它自适应，步伐开始大，后面每步只能越来越小，这样就解决了如果学习率太大，可能冲过目标点，太小又下降的太慢的问题

$$W_{(t)i}=W_{(t-1)i}+\frac{\eta }{\sqrt{S_{(t)}+ϵ}}{V}_t$$$$S_{(t)}=S_{(t-1)}+\Delta W_{(t)i}\cdot \Delta W_{(t)i}$$

• $ϵ$ 是极小量，为了避免分母是0
• S(t) 有参考历史梯度，相对于每一步上，梯度越大走的步伐增量越小；梯度越小，走的步伐相对来说增量大一点；但整体来看 整体分母是不断增加的，就是增加的量是变化的，整体看步伐只会是越来越小。

缺点：整体看步伐只会是越来越小，导致这种步伐一单变的很小了，就没办法再增大了，再次遇到大梯度就下降的很慢

---

4.6 RMSprop

对上面的缺点进行了优化，就是和动量想法相似，利用历史数据，但是越近的影响越大(方法的解释在第16分钟)

$$W_{(t)i}=W_{(t-1)i}+\frac{\eta }{\sqrt{S_{(t)}+ϵ}}{V}_t$$$$S_{(t)}=\beta \cdot S_{(t-1)}+（1-\beta ）\Delta W_{(t)i}\cdot \Delta W_{(t)i}$$

---

4.7 Adam

动量法(梯度的优化)+RMSprop(学习率优化) = Adam
$$W_{(t)i}=W_{(t-1)i}+\frac{\eta }{\sqrt{S_{(t)}+ϵ}}{V}_t$$$$V_t={\beta }_1\cdot V_{t-1}+(1-{\beta }_1)\cdot d{w}_{(t)i}$$$$S_{(t)}={\beta }_2\cdot S_{(t-1)}+（1-{\beta }_2）\Delta W_{(t)i}\cdot \Delta W_{(t)i}$$