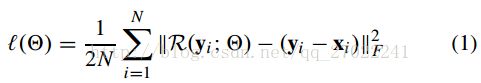DnCNN论文阅读笔记【MATLAB】
DnCNN论文阅读笔记
论文信息:
论文代码:https://github.com/cszn/DnCNN
Abstract
提出网络:DnCNNs
关键技术: Residual learning and batch normalization 残差学习和批归一化
解决问题: Gaussian denoising (nonblind and blind)
Single image super-resolution(SISR )
Single image super-resolution(SISR )
JPEG image deblocking 解压缩
I. Introduction
之前的进展:
(1)various models have been exploited for modeling image priors
缺点:测试阶段包含复杂的优化问题,耗时;
模型一般为非凸,且包含很多超参数,很难达到最优性能。
(2)several discriminative learning methods
缺点:显式学习图像先验
包含很多超参数,很难达到最优性能
一个噪声水平训练一个模型,受限于盲图像去噪
本文使用CNN的3个原因:
(1)深网络可以有效提高利用图像特征的容量和灵活性;
(2)CNN训练正则和学习方法有相当大的提升,例如:Rectifier Linear Unit (ReLU)、batch normalization and residual learning,可以加速训练过程,提高去噪性能;
(3)GPU并行计算可提高运行速度。
本文创新:
(1)提出一个端到端的可训练的CNN网络,采用残差学习策略,在网络的隐层隐式地移除干净图片(clean image)。即输入为带噪的观测图片(noisy image),输出为移除了干净图片的残差(噪声)图片(residual image)。这样做的动机是,用残差学习刻画恒等映射或近似的恒等映射,效果要比直接学习干净图片要相对好;
(2)采用残差学习和批归一化加速训练并提升性能;
(3)训练可以进行盲图像去噪的单一模型;
训练单一模型解决三类图像去噪问题:blind Gaussian denoising, SISR, and JPEG deblocking。单图像超分辨问题(SISR)和去块效应问题都是降噪问题的特例。一般化的模型可以一起解决这些问题。
II. Related Work
A. Deep Neural Networks for Image Denoising (a specific model is trained for a certain noise level)
(1)the multilayer perceptron (MLP) [31]
(1)the multilayer perceptron (MLP) [31]
(2)a trainable nonlinear reaction diffusion (TNRD) model [19]
B. Residual Learning and Batch Normalization
(1)Residual Learning
(2)Batch Normalization
III.The Proposed Denoising CNN Model
Training a deep CNN model for a specific task generally involves two steps:
(1) network architecture design
修改VGG网络 [26]并设置网络深度
(2) model learning from training data
使用the residual learning,batch normalization 加速训练并提升去噪性能
A. Network Depth
滤波器尺寸3*3,但去除所有的池化层。故对于d层的DnCNN ,感受野为(2d+1)(2d+1)。
确定感受野的大小:
(1)其他经典方法中的感受野对比:
For Gaussian denoising with a certain noise level, we set the receptive field size of DnCNN to 35×35 with the corresponding depth of 17.
For other general image denoising tasks, we adopt a larger receptive field and set the depth to be 20.
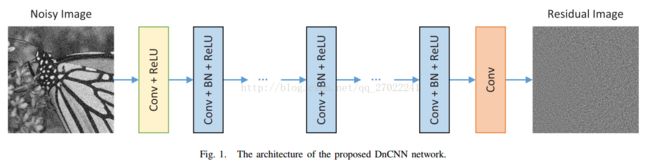
B. Network Architecture
For DnCNN, we adopt the residual learning formulation to train a residual mapping R(y)≈ v, and then we have x = y- R(y).
The loss function(the averaged mean squared error between the desired residual images and estimated ones from noisy input) to learn the trainable parameters :
:
(1)Deep Architecture
深度为D的网络包含三种类型的层:
(i) Conv+ReLU: for the first layer, 64 filters of size 3× 3 ×c are used to generate 64 feature maps, and rectified linear units (ReLU,max(0,·)) are then utilized for nonlinearity. Herec represents the number of image channels,
i.e., c = 1 for gray image and c = 3 for color image.
i.e., c = 1 for gray image and c = 3 for color image.
(ii)Conv+BN+ReLU: for layers 2 ∼ (D- 1), 64 filters of size 3×3×64 are used, and batch normalization is added
between convolution and ReLU.
between convolution and ReLU.
(iii)Conv: for the last layer, c filters of size 3 ×3 × 64 are used to reconstruct the output.
(2)Reducing Boundary Artifacts
In many low level vision applications, it usually requires that the output image size should keep the same as the input one. This may lead to the boundary artifacts.
We directly pad zeros before convolution to make sure that each feature map of the middle layers has the same size as the input image.
C. Integration of Residual Learning and Batch Normalization for Image Denoising

It is the integration of residual learning formulation and batch normalization rather than the optimization algorithms (SGD or Adam) that leads to the best denoising performance.
D. Connection With TNRD
略
E. Extension to General Image Denoising
(1)DnCNN for Gaussian denoising with unknown noise level
(1)DnCNN for Gaussian denoising with unknown noise level
In the training stage, we use the noisy images from a wide range of noise levels (e.g.,σ ∈ [0,55]) to train a single DnCNN model. Given a test image whose noise level belongs to the noise level range, the learned single DnCNN
model can be utilized to denoise it without estimating its noise level.
model can be utilized to denoise it without estimating its noise level.
(2)three specific tasks, i.e., blind Gaussian denoising, SISR, and JPEG deblocking three specific tasksby employing the proposed DnCNN method
In the training stage, we utilize the images with AWGN from a wide range of noise levels, down-sampled images with multiple upscaling factors, and JPEG images with different quality factors to train a single DnCNN model.
IV. Experimental Results
IV. Experimental Results
A. Experimental Setting
1. Training and Testing Data:
(1)DnCNN-S (for Gaussian denoising with known specific noise level )
Three noise levels:σ = 15, 25 and 50
Follow [19] to use 400 images of size 180×180 for training
Set the patch size as 40×40, and crop 128×1,600 patches to train the model
(2)DnCNN-B (single DnCNN model for blind gray Gaussian denoising task )
Set the patch size as 40×40, and crop 128×1,600 patches to train the model
(2)DnCNN-B (single DnCNN model for blind gray Gaussian denoising task )
Set the range of the noise levels asσ ∈ [0,55]
Set the patch size as 50× 50 and crop 128×3,000 patches to train the model
Two test datasets: 68 natural images from Berkeley segmentation dataset (BSD68) [14]
the other one contains 12 images as shown in Fig. 3
(3)CDnCNN-B (single DnCNN model for blind color Gaussian denoising task )
(3)CDnCNN-B (single DnCNN model for blind color Gaussian denoising task )
Set the range of the noise levels asσ ∈ [0,55]
Set the patch size as 50× 50 and crop 128×3,000 patches to train the model
Use color version of the BSD68 dataset for testing and the remaining 432 color images from Berkeley segmentation dataset are adopted as the training images
Use color version of the BSD68 dataset for testing and the remaining 432 color images from Berkeley segmentation dataset are adopted as the training images
(4)DnCNN-3 (single DnCNN model for these three general image denoising tasks )
Set the patch size as 50× 50 and crop 128×3,000 patches to train the model
Rotation/flip based operations on the patch pairs are used during mini-batch learning.
The parameters are initialized with DnCNN-B
Training set: 91 images from [43] and 200 training images from the Berkeley segmentation dataset
三种去噪任务的输入分别为:
1) The noisy image is generated by adding Gaussian noise with a certain noise level
from the range of [0,55].
from the range of [0,55].
2) The SISR input is generated by first bicubic downsampling and then bicubic upsampling the high-resolution image with downscaling factors 2, 3 and 4.
3) The JPEG deblocking input is generated by compressing the image with a quality factor ranging from 5 to 99 using the MATLAB JPEG encoder.
2. Parameter Setting and Network Training
3) The JPEG deblocking input is generated by compressing the image with a quality factor ranging from 5 to 99 using the MATLAB JPEG encoder.
2. Parameter Setting and Network Training
Set the network depth to 17 for DnCNN-S and 20 for DnCNN-B and DnCNN-3
initialize the weights by the method in [34] and use SGD with weight decay of 0.0001, a momentum of 0.9 and a mini-batch size of 128. We train 50 epochs for our DnCNN models.
The learning rate was decayed exponentially from 1e- 1 to 1e- 4 for the 50 epochs.
B. Compared Methods
two non-local similarity based methods (i.e., BM3D [2] and WNNM [15])
one generative method (i.e.,EPLL [40])
three discriminative training based methods (i.e., MLP [31],CSF [17] and TNRD [19])
C. Quantitative and Qualitative Evaluation
略
C. Quantitative and Qualitative Evaluation
略
D. Run Time
E. Experiments on Learning a Single Model for Three General Image Denoising Tasks
V. Conclusion
In future, we will investigate proper CNN models for denoising of images with real complex noise and other general image restoration tasks.