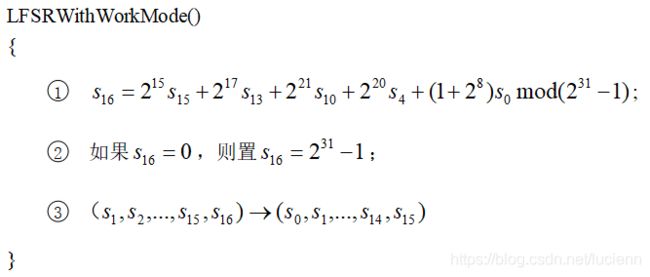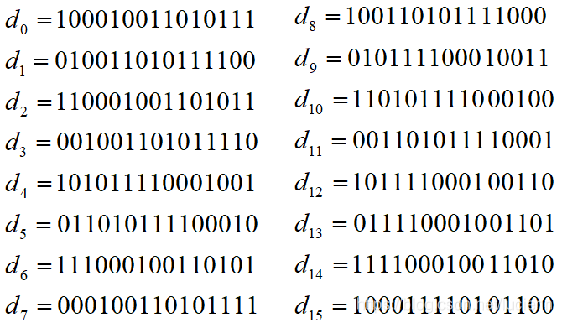ZUC算法

---

前言

ZUC算法是国密算法的一种，它是一种同步序列密码，在实际应用中可以用来替换RC4算法。

---

提示：以下是本篇文章正文内容，下面案例可供参考

1. ZUC算法简介

   祖冲之算法集是由我国学者自主设计的加密和完整性算法，包括祖冲之算法（ZUC)、加密算法128-EEA3和完整性算法128-EIA3。
   ZUC 算法属于同步序列密码，其也是中国第一个成为国际密码标准的密码算法。2011年9月19-21日，在日本福冈召开的第53次第三代合作伙伴（3GPP）系统架构组（SA）会议上，我国设计的祖冲之密码算法（ZUC）被批准成为新一代宽带无线移动通信系统（LTE）国际标准，即4G的国际标准。

2. ZUC算法结构

ZUC算法在逻辑上分为上中下三层。上层是16级线性反馈移位寄存器（LFSR），中层是比特重组（BR），下层是非线性函数F。

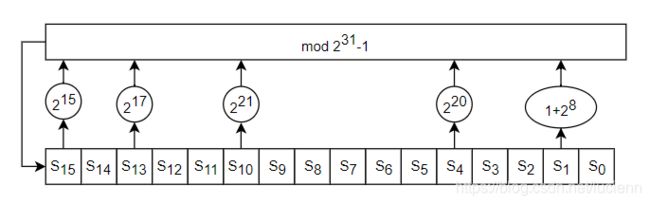
2.1 LFSR

³¹上层的LFSR由16个31比特寄存器单元变量组成，每个变量在集合{1,2,3,…,2³¹-1}中取值。线性反馈移位寄存器以有限域GF（2³¹-1）上的16次本原多项式

P(X)=x ¹⁶-2 ¹⁵x ¹⁵-2 ¹⁷x ¹³-2 ²¹x ¹⁰-2 ²⁰x ⁴-(2 ⁸+1)

为连接多项式。因此，输出为素域GF（2³¹-1）上的m序列，具有良好的随机性。

【注】m序列是最长线性反馈移位寄存器序列的简称。它是由带线性反馈的移存器产生的周期最长的序列。一般来说，在二元域上，一个n级线性反馈移存器可能产生的最长周期等于(2ⁿ -1)。这里的LFSR是在有限域GF（2³¹-1）上定义的，因此，其输出的m序列的周期为(2³¹-1)¹⁶-1，约等于2⁴⁹⁶，这是相当大的。

线性反馈移位寄存器的运行模式有两种：初始化模式和工作模式。

2.1.1 初始化模式

在初始化模式下，LFSR接收一个31比特字u。u是由非线性函数F的32比特输出W通过舍弃最低为比特得到。

2.1.2 工作模式

在工作模式下，LFSR不接受任何输入。

比较初始化模式和工作模式可知，二者的差异在于初始化时需要引入由非线性函数F输出W通过舍弃最低为比特得到的u，而工作模式不需要。初始化模式引入非线性函数F的输出u的目的是使线性反馈移位寄存器的状态随机化。

2.2 BR

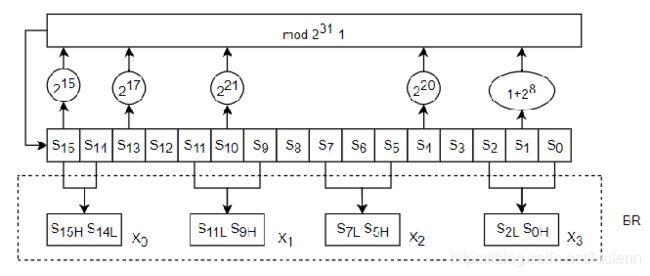
中层的比特重组从LFSR的寄存器单元中抽取128比特组成4个32比特字X0、X1、X2、X3。比特重组的具体计算过程如下：

H：取字的高16比特    L: 取字的低16比特

【注】:这里注意一下，由于寄存器中的值s_i为31比特，很多书上的示例都是以16进制来写s_i的值。例如：s₁₅=0047ac00,s₁₄=00789a00，则X₀=008f9a00。
低16位可以直接取s₁₄的后两个字节，即9a00，但高16位要将0047ac00化为二进制，再取值。因为这里的s是31位而不是32位。

  比特重组采用取半合并技术，实现LFSR数据单元到非线性函数F和密钥输出的数据转换，其主要目的是破坏LFSR在素域GF(2³¹-1)上的线性结构。

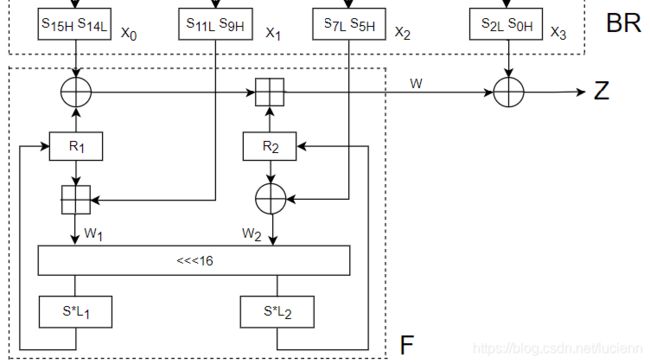
2.3 非线性F函数

R₁、R₂：32位存储单元

田：表示 mod 2³² 加法

S盒：由4个并置的8进8出S盒构成，其中S₂=S₀，S₃=S₁，于是有S=（S₀，S₁，S₀，S₁）

L₁、L₂：非线性函数


  非线性函数F内部包含2个32比特存储单元R₀和R₁，F的输入为来自比特重组的3个32比特字X₀、X₁、X₂，输出为一个32比特字W。因此，非线性函数F是一个把96比特压缩为32比特的一个非线性压缩函数。

函数F的具体计算过程如下：


  首先是将X₀与R₁异或得到的值与R₂做mod 2³²加法，得到W。这个W除去最低的一个比特位，就是LFSR在初始化模式下的输入值u。然后由R₁与X₁mod 2³²加得到W₁，R₂和X₂异或得到W₂。再将W₂的低16比特与W₂的高16比特做连接，经过L₁函数计算以及S盒变化，得到R₁，同理，得到R₂。

S盒变化的过程如下：
  假设经过L₁计算得到的32比特值的16进制为ef897a4c，则将ef、89、7a、4c分别送到S₀、S₁、S₀、S₁中进行查询，其中高位为行数，低位为列数。例如ef在S₀中查询，则得到的是e行f列的值。

3 ZUC算法流程

3.1 密钥装入

密钥装入过程将128比特的初始密钥KEY和128比特的初始向量IV扩展为16个31比特字作为LFSR寄存器单元变量s₀,s₁,…,s₁₅的初始状态。其中：

KEY=k ₀ || k ₁||......|| k ₁₅ IV=iv ₀ || iv ₁||......|| iv ₁₅

其中，k_i和iv_i均为8比特字节

密钥装入过程如下：
引入一个240比特的常量D，按照下列方式将其分为16个15比特的子串：

D= d ₀ || d ₁||......|| d ₁₅

其中，d_i的表示可以为：

3.2 算法运行

3.2.1 初始化阶段

1. 把128比特的KEY和128比特IV按照上面的密钥装入方法装入到LFSR的寄存器单元变量中;
2. 置非线性函数F中的R1、R2全为0;
3. 重复下面过程32次:

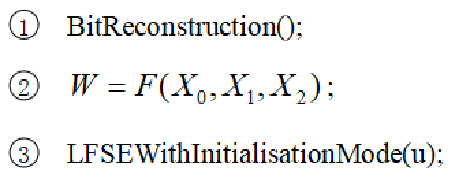
因为寄存器中已经有值了，所以可以进行比特运算，然后再进行F运算，得到W。之后再进行LFSR的初始化模式计算。

3.2.2 工作模式

1. 首先执行下列过程各一次，并将F的输出W舍弃：
   
2. 在密钥输出阶段，每运行一个节拍，执行下列过程一次，并输出一个32比特的密钥字Z：
   

4. ZUC算法安全性

1. 在LFSR设计上

ZUC 算法的 LFSR 设计首次采用素域 GF(2³¹ - 1) 的 m 序列。该类序列周期长、统计特性好。此外，由于素域 GF(2³¹ - 1)上的乘法可以快速实现，LFSR 在设计时充分考虑到安全和效率两方面的问题，在达到高安全目标的同时可以拥有非常高效地软硬件实现。

2. 在BR设计上

在比特重组部分，精心选用数据使得重组的数据具有良好的随机性，并且出现重复的概率足够小。

3. 在F函数设计上

在非线性函数F 的设计上，F函数采用了两个非线性变换S盒S0和S1，从而为祖冲之密码提供了非线性。又由于LFSR和BR都是线性变换，所以非线性函数F就成为ZUC算法中唯一的非线性部件，从而成为确保ZUC算法安全的关键。其中，S盒为密码提供混淆作用，L为密码提供扩散作用，二者互相配合提高密码安全性。

总结

以上就是ZUC算法的具体介绍，希望能对读者有所帮助。