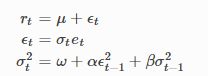关于Python的ARCH包（二）

1.单变量波动率模型
1.1引言
1.2 举例
1.3 预测

1.4 预测举例

1.5 预测类型
1.6 均值模型

1.7 波动率过程

1.8 不变方差过程
1.9 分布

1.10 背景及引用

---

1.1 关于ARCH 模型的介绍

 

1.1.1理论模型

ARCH 模型是一种流行的波动率建模方法，其主要使用收益率或残差的观测值作为波动率参考方式。一种基本的GARCH 模型表示如下：

 

完整的GARCH模型需要上述三个部分，然而简单的计算可以利用下式得出：

import datetime as dt

import pandas_datareader.data as web

from arch import arch_model

start = dt.datetime(2000, 1, 1)
end = dt.datetime(2014, 1, 1)
sp500 = web.DataReader('^GSPC', 'yahoo', start=start, end=end)
returns = 100 * sp500['Adj Close'].pct_change().dropna()
am = arch_model(returns)

注：实际无法运行，由于Yahoo网络变动，导致出现提示：

ImmediateDeprecationError: 
Yahoo Daily has been immediately deprecated due to large breaks in the API without the
introduction of a stable replacement. Pull Requests to re-enable these data
connectors are welcome.

See https://github.com/pydata/pandas-datareader/issues

使用其他收益率数据后，可直接运行：

from arch import arch_model

am = arch_model(returns)

也可从结构设计开始手动构建ARCH模型：

from arch import ConstantMean, GARCH, Normal

am = ConstantMean(returns)
am.volatility = GARCH(1, 0, 1)
am.distribution = Normal()

-----

这几行代码已经无法正常使用，应该是升级导致。因此，直接的使用应该是：

am = arch_model(abc3.iloc[1:800,:])
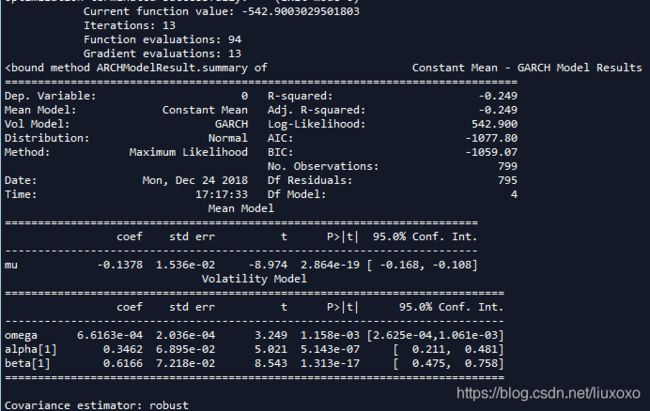
res=am.fit() #拟合

res.summary#拟合结果

1.1.2 关键内容：关于arch_model方法

---

arch.arch_model(y, x=None, mean='Constant', lags=0, vol='Garch', p=1, o=0, q=1, power=2.0, dist='Normal', hold_back=None)[source]

使用便利函数以便arch模型快速初始化：

Parameters:	y ({ndarray, Series, None}) – 因变量 x ({np.array, DataFrame}, optional) –外生变量.如果没有外生变量则模型自动省略。 mean (str, optional) – 均值模型的名称.目前支持: ‘Constant’, ‘Zero’, ‘ARX’ 以及 ‘HARX’ lags (int or list (int), optional) –一个整数标量，用来表明滞后阶，或者使用表明滞后位置的整数列表。 vol (str, optional) – 波动率模型的名称，目前支持: ‘GARCH’ （默认）, ‘ARCH’, ‘EGARCH’, ‘FIARCH’ 以及 ‘HARCH’。 p (int, optional) – 对称随机数的滞后阶（译者注：即扣除均值后的部分）。 o (int, optional) – 非对称数据的滞后阶 q (int, optional) – 波动率或对应变量的滞后阶 power (float, optional) – 使用GARCH或相关模型的精度 dist (int, optional) – 误差分布的名称，目前支持下列分布： 正态分布: ‘normal’, ‘gaussian’ (default) 学生T分布: ‘t’, ‘studentst’ 偏态学生T分布: ‘skewstudent’, ‘skewt’ 通用误差分布: ‘ged’, ‘generalized error” hold_back (int) – 估计模型参数时样本最初需排除的观察值数. 对同一样本使用不同的滞后阶来比较模型时使用该参数。
Returns:	model – Configured ARCH model
Return type:	ARCHModel

除了直接使用arch_model以外，也可以具体表明GARCH参数来描述均值及波动率模型：

am = arch_model(returns, mean='AR', lags=2, vol='harch', p=[1, 5, 22])

下面可以是一个0均值，TGARCH模型，误差为学生T分布的通用ARCH模型：

am = arch_model(returns, mean='zero', p=1, o=1, q=1, power=1.0, dist='StudentsT')

注意：

输入内容并非特指，均值为0的滞后期设定等，默认忽略。

模型结果

所有模型返回同样的对象，即结果类(ARCHModelResult)

---

---

1.1.3 ARCHModelResult

class arch.univariate.base.ARCHModelResult(params, param_cov, r2, resid, volatility, cov_type, dep_var, names, loglikelihood, is_pandas, optim_output, fit_start, fit_stop, model)[source]

 ARCHModel 模型的估计结果

Parameters:

params (ndarray) – 估计参数 param_cov ({ndarray, None}) – 估计参数的方差协方差矩阵.如果为空，则表示使用方法基于参数协方差来计算模型方差。 r2 (float) – 模型R2（即可决系数或判决系数） resid (ndarray) – 模型残差。残差矩阵大小相同，并包括估计中未使用的空值。 volatility (ndarray) – 来自模型的条件波动率。 cov_type (str) – 描述协方差估计值的字符串。 dep_var (Series) – 因变量。 names (list (str)) – 模型参数名称。 loglikelihood (float) – 估计参数的对数似然率。 is_pandas (bool) – 判断原始输入数据是否是pandas类型。 fit_start (int) – 用来拟合模型的第一个观察值的整数索引。 fit_stop (int) – 最后一个观察值的整数索引，切片表示： fit_start:fit_stop model (ARCHModel) – 用来估计参数的模型。

 

summary() [source] :对结果进行汇总。

plot() ：对波动率和标准化的残差进行绘图。

conf_int()[source] ：置信区间。

loglikelihood ：浮点型，对数似然率的值。

params ：时间序列类型，估计所得参数。

param_cov ：DataFrame类型，估计参数的方差协方差。

resid ：{ndarray, Series}：观察值数组，包括模型残差。

modelARCHModel –Model：用来拟合的模型实例

conf_int(alpha=0.05)[source]

Parameters:	alpha (浮点型,可选) – 构建置信区间的规模（即概率）.
Returns:	ci – 数组型，第i行包括第i个参数的置信区间。
Return type:	ndarray（n维数组型）

forecast (params=None, horizon=1, start=None, align='origin', method='analytic', simulations=1000, rng=None)

利用估计所得模型参数进行预测

Parameters:	params (ndarray, optional) –使用的替代参数。如为空，则使用模型拟合的参数，其大小必须与模型拟合所得参数一致。 horizon (int, optional) – 预测步数。 start ({int, datetime, Timestamp, str}, optional) – 一个整数型，日期型或字符串型数据，表示用作预测的第一个观察值。日期型仅仅适用于具有日期型索引的pandas类型数据。字符串型必须可以转换为日期型数据，比如 ‘1945-01-01’. align (str, optional) – 为 ‘origin’ 或 ‘target’. 当为 ‘origin’时，第t行预测包括的预测值为 t+1, t+2, …, t+h. 当为‘target’时，第t行以t-1行为基础进行1步式预测，t-2行为基础进行2步式预测，或以t-h为基础进行h步预测。 如选择h步预测，‘target’方式简化了预测误差计算。  method ({'analytic', 'simulation', 'bootstrap'}, optional) – 执行预测的方法。默认为解析型 （analytic）.该方法仅仅影响预测结果的方差。 并非全部波动率模型支持全部方法。比如，波动率模型并不支持平方模式下的变化，比如EGARCH 或者TARCH， 这些方法当预测步数大于1时不再支持‘analytic’ 方法。 simulations (int, optional) – 使用模拟或拔靴等方法计算预测结果的次数。 rng (callable, optional) – 基于模拟预测的自主随机数生成器方式。当使用rng语法用于2维元组（simulations,horizon）时，必须生成随机样本。
Returns:	forecasts – t*h data frame 的预测结果。其预测或计算方式由align参数控制。
Return type:	ARCHModelForecast

注意：

最基本的1步式预测将会返回与原始数据同维的向量，这里第t个值即为用于t+1时间预测的值。当步数大于1时且计算方式默认时，在 [t, h] 处的预测值即为在t时间, h+1步的预测值。

如果模型包括外生变量（model.x非空）,那么仅仅有1步式预测可用。当步数 > 1时，将会出现提示，且所有列除第一列外，全部为空。

如果计算方式为 ‘origin’,[t,h] 预测值基于y[:t] 预测且步数为h+1(那就是说，截至但不包括t). 例如，y[100,2] 表示使用前100个数据点进行3步式预测，即实现结果为 y[100 + 2]. 如果计算方式是 ‘target’, 那么同样的预测表示为 [102, 2]。这样是为了与原始数值一致便于比较，但是仍然在同一列中。

hedgehog_plot(params=None, horizon=10, step=10, start=None, type='volatility', method='analytic', simulations=1000)
基于估计模型将预测结果图形化。

Parameters:

params ({ndarray, Series}) – 使用的替代参数.如果不填写，将使用模型拟合参数。其须是1维且与拟合模型的参数大小一致。 horizon (int, optional) – 预测步数。 step (int, optional) – 不同的样条之间预测步数需跳过的非空预测。 start (int, datetime or str, optional) – 一个整数，日期或字符串数据，表示预测数据使用的第一个观察值。日期型选项仅仅用于使用日期索引的pandas数据。字符串必须可转化为日期型，比如 ‘1945-01-01’. 如果不填写，则计算起始点被设置为最早可使用观察值。 type ({'volatility', 'mean'}) – 数量到图，预测波动率或预测平均值。 method ({'analytic', 'simulation', 'bootstrap'}) – 进行预测时使用的方法，默认为解析方法。该方法仅仅影响预测结果位置的方差。并非所有波动率模型支持所有方法。比如，波动率模型并不支持平方模式下的变化，比如EGARCH 或者TARCH， 这些方法当预测步数大于1时不再支持‘analytic’ 方法。 simulations (int) – 使用模拟或拔靴等方法计算预测结果的次数。

Returns:	fig – 图形手柄
Return type:	图形

Examples

>>> import pandas as pd
>>> from arch import arch_model
>>> am = arch_model(None,mean='HAR',lags=[1,5,22],vol='Constant')
>>> sim_data = am.simulate([0.1,0.4,0.3,0.2,1.0], 250)
>>> sim_data.index = pd.date_range('2000-01-01',periods=250)
>>> am = arch_model(sim_data['data'],mean='HAR',lags=[1,5,22],  vol='Constant')
>>> res = am.fit()
>>> fig = res.hedgehog_plot(type='mean')

plot(annualize=None, scale=None)

标准化残差或波动率的图形化展示

Parameters:	annualize (str, optional) – 数据频率的字符串，表明图形应该年华波动率，支持 ‘D’ (daily), ‘W’ (weekly) and ‘M’ (monthly), 表示大小分别为 252, 52, 和 12。 scale (float, optional) – 年化收益时使用的值.如提供数值，则表示忽略年化，使用实际值。
Returns:	fig – 图形手柄
Return type:	图形

举例：

>>> from arch import arch_model
>>> am = arch_model(None)
>>> sim_data = am.simulate([0.0, 0.01, 0.07, 0.92], 2520)
>>> am = arch_model(sim_data['data'])
>>> res = am.fit(update_freq=0, disp='off')
>>> fig = res.plot()

使用年化波动率画图：

>>> fig = res.plot(annualize='D')
使用252日代替360日画图，以便更符合实际：
>>> fig = res.plot(scale=360)

summary()[source]

构建模型拟合结果.

Returns:	summary – 对象，包括表格以及便利输出类内容，诸如 text, html or latex
Return type:	结果实例

如果使用 fix 方法, 该对象 (ARCHModelFixedResult) 与另一对象 (ARCHModelResult)不同，两者在参数没有估计时不存在相关关系。

1.1.4 ARCHModelFixedResult

class arch.univariate.base.ARCHModelFixedResult(params, resid, volatility, dep_var, names, loglikelihood, is_pandas, model)[source]

对于固定参数ARCH模型的估计结果

Parameters:	params (ndarray) –估计参数 resid (ndarray) – 模型残差。残差结果与原始数据大小一致，且包含未在估计中使用的空值。 volatility (ndarray) – 模型的条件波动率 dep_var (Series) – 因变量 names (list (str)) – 模型参数名 loglikelihood (float) – 参数的对数似然率 is_pandas (bool) – 原始输入是否是pandas类型 model (ARCHModel) – 所要估计的模型

summary()  source] ：汇总结果。

plot()[source]

对波动率和标准化残差画图。

forecast()[source]

利用模型构建预测。

loglikelihood

float – 对数似然值

params

Series – 所估计参数。

resid

{ndarray, Series} – 包括模型残差的观察值数组。

model

ARCHModel – 用于拟合的模型实例。

 

forecast(params=None, horizon=1, start=None, align='origin', method='analytic', simulations=1000, rng=None)[source]

利用估计模型进行预测。

Parameters:	params (ndarray, optional) – 使用的替代参数。如果没有赋值，则使用模型拟合估计参数，且该参数大小必须与拟合模型参数一致。 horizon (int, optional) – 预测步数。 start ({int, datetime, Timestamp, str}, optional) – 为整数型，日期型或者字符串型，为用于预测的第一个观察值。日期型仅仅适用于具有日期索引的pandas类型数据，字符串型必须可以转化为日期型，比如 ‘1945-01-01’. align (str, optional) – 为原始或者目标两种方式。当设定为原始型时，第t行的预测包括预测值的位置为 t+1, t+2, …, t+h. 当设定为目标型时，第t行包括在t-1时的第1步预测，第2步包括在t-2时的预测等等诸如此类，即第h步来自t-h时点.既然h步预测和实现得以实现的话，目标型方式简化描述了预测误差。  method ({'analytic', 'simulation', 'bootstrap'}, optional) – 用于预测的方法，默认为解析方法。该方法仅影响预测结果的方差。并非所有波动率模型支持所有方法。尤其是，波动率模型并不能解决平方项，比如EGARCH或TARCH就不支持预测步数大于1的解析方法。 simulations (int, optional) – 模拟或自举的次数。 rng (callable, optional) – 基于模拟预测的自主随机数生成器。当大小为2维元组类型时（模拟机预测步数），必须使用rng(size)语法生成自主随机样本。
Returns:	forecasts – t*h大小的dataframe格式的预测结果。该预测的方法由align参数控制。
Return type:	ARCHModelForecast

注意：

最基本的1步式预测会返回与原始数据同样长度的向量，且第t个值为t时对于t+1时的预测。当预测步数大于1时且使用默认align方式，[t,h]的预测值即是时间t对h+1步的预测。

如果模型包括外生变量（model.x为非空），则仅有1步式预测可用。预测步数大于1时将会产生警示信息，所有列除第1列外，将会被空值填充。

如果align方式为原始方法，对于步数h + 1，预测结果[t,h]包括数据 y[:t] (即趋近t但不包括t). 例如， y[100,2] 为3步式预测，使用前100个数据点，对应结果 y[100 + 2]. 如果选择 ‘target’方法, 那么同样的预测位置为 [102, 2], 因此与预测时使用的原始数据一致，但是仍然为同一列。

hedgehog_plot(params=None, horizon=10, step=10, start=None, type='volatility', method='analytic', simulations=1000)[source]

Plot forecasts from estimated model

Parameters:	params ({ndarray, Series}) – 替代选择参数。如果没有赋值，则使用模型拟合参数。该参数为1维且与模型拟合的参数一致。 horizon (int, optional) – 预测步数。 step (int, optional) – 样条之间需要略过的预测非负值。 start (int, datetime or str, optional) – 一个整数，日期或字符串型参数，用于表示使用的第1个观察值。日期型仅仅适用于pandas型且使用日期索引的数据。字符串必须可以转换为日期型，比如‘1945-01-01’. 如果没有赋值，则起始点为最早预测日期。 type ({'volatility', 'mean'}) – 绘图数，为波动率或者预测均值。 method ({'analytic', 'simulation', 'bootstrap'}) – 用于预测的方法，默认为解析方法。该方法仅仅影响预测结果的方差。并非所有波动率模型支持所有方法。尤其是，波动率模型并不支持平方项，如 EGARCH 或 TARCH就不支持在支持步数大于1的解析方法。 simulations (int) – 自举或者模拟的次数。
Returns:	fig – 绘图手柄。
Return type:	图像

举例：

>>> import pandas as pd
>>> from arch import arch_model
>>> am = arch_model(None,mean='HAR',lags=[1,5,22],vol='Constant')
>>> sim_data = am.simulate([0.1,0.4,0.3,0.2,1.0], 250)
>>> sim_data.index = pd.date_range('2000-01-01',periods=250)
>>> am = arch_model(sim_data['data'],mean='HAR',lags=[1,5,22],  vol='Constant')
>>> res = am.fit()
>>> fig = res.hedgehog_plot(type='mean')

plot(annualize=None, scale=None)[source]

标准化残差及条件波动率的图示。

Parameters:	annualize (str, optional) –包括年化波动率的数据频率图示字符串，支持 ‘D’ (daily)型, ‘W’ (weekly)型 及 ‘M’ (monthly)型，分别表示252, 52和12日情况下的方差。 scale (float, optional) – 年化收益使用的参数，如果该参数被赋值，年化参数以实际赋值为准。
Returns:	fig – 绘图手柄
Return type:	图像

举例

>>> from arch import arch_model
>>> am = arch_model(None)
>>> sim_data = am.simulate([0.0, 0.01, 0.07, 0.92], 2520)
>>> am = arch_model(sim_data['data'])
>>> res = am.fit(update_freq=0, disp='off')
>>> fig = res.plot()

年化波动率图：

>>> fig = res.plot(annualize='D')

以360日代替惯常使用的 252 日来画图：

>>> fig = res.plot(scale=360)

summary()[source]

拟合结果：

Returns:	summary –包括表格以及文本，html和latex等便利输出内容。
Return type:	结果实例