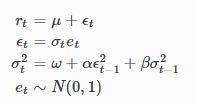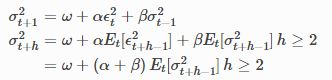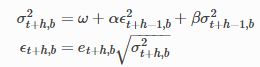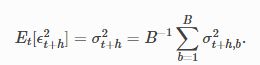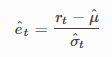关于Python的ARCH包（四）
1.3 举例
参考附加说明，使用递归可以利用ARCH类模型方便的进行多期预测。在特定情况下，那些不与平方项或残差同步的模型并不具有可追踪的正态解析多期预测。
所有模型支持三种预测方式：
- 解析：基于ARCH类型的结果，解析预测方法对1步式预测总是可用的；多步解析预测方法仅仅适用于对残差平方项呈线性关系的模型，比如 GARCH 或者 HARCH.
- 模拟：虽然基于模拟方法的预测对任何步数都可用，但是基于ARCH类型的第一个样本外预测不变，模拟预测方法仅仅适应于步数大于1的情况。模拟预测利用了ARCH类型的结构，并假设残差服从一定分布，例如正态分布或学生T分布等进行模拟。
- 自举：自举方法在估计中利用了源自实际数据的标准化残差而非假定分布， 其他则与模拟预测方法类似。与模拟预测方法一样，自举预测仅仅对步数大于1的情况有效。此外，自举预测方法需要一个最小样本内数量以便产生预测结果。
本文将使用常数均值的标准GARCH(1,1)过程来解释预测方法。该模型可以表述如下：
代码中使用了标准普尔500指数数据：
（注：返回以下出错提示，具体测试时可以使用自己的数据，导入即可）
ImmediateDeprecationError:
Yahoo Actions has been immediately deprecated due to large breaks in the API without the
introduction of a stable replacement. Pull Requests to re-enable these data
connectors are welcome.
See https://github.com/pydata/pandas-datareader/issuesfrom arch import arch_model
import datetime as dt
import pandas_datareader.data as web
start = dt.datetime(2000,1,1)
end = dt.datetime(2014,1,1)
sp500 = web.get_data_yahoo('^GSPC', start=start, end=end)
returns = 100 * sp500['Adj Close'].pct_change().dropna()
am = arch_model(returns, vol='Garch', p=1, o=0, q=1, dist='Normal')该模型将使用前10年数据估计参数，然后对最后5年进行预测。
split_date = dt.datetime(2010,1,1)
res = am.fit(last_obs=split_date)1.3.1 解析预测
解析预测对于大多数与残差平方项线性相关的模型，比如 GARCH, HARCH等等。这些预测方法利用了
等式的关系，递归计算预测结果。对于条件方差的方差预测构建模型如下：
forecasts = res.forecast(horizon=5, start=split_date)
forecasts.variance[split_date:].plot()1.3.2 模拟预测
基于模拟的预测使用随机数生成器来模拟标准化的残差数据流，比如, 
这些随机数被用于生成预先定义路径的方差，然后平均化方差用于预测。在线性GARCH类模型中，与模拟预测相比并无很多亮点。这些方法在利用如EGARCH等多步模型进行多步预测时更有价值。
假定存在BB模拟路径，一个单路径模拟过程如下：
这里模拟冲击为 
，且 bb 表明独立的模拟路径。注意，第一个残差
，是样本残差，因而并非模拟得出。
最终预测的方差经过BB模拟后得出。
forecasts = res.forecast(horizon=5, start=split_date, method='simulation')1.3.3 自举预测
自举预测（也称拔靴预测）除了标准化的残差由模型生成意外，本质与模拟预测一致。标准化的残差由观察值生成，估计参数为：
除了模拟冲击（使用正态分布替换）来自
，其他与模拟预测方法一致。因此，仅仅t时刻的数据用于模拟路径。
1.3.4 预测参数
预测方法 forecast() 是模型拟合结果方法的子方法。
params- 该模型参数用于预测均值和方差。如果没有指明，则使用拟合结果的参数.horizon- 正整数值，表示预测最大步数。start-正整数值，或者输入模式为DataFrame格式的日期型数据（string，date或datetime64或Timestamp）。预测自start起至样本最终结束。如果没有指明，start设定为数据长度减1，也就是一步式预测。align- 原始（默认）或者目标两种方法，表明预测使用的结果表述方式。原始选项将预测对齐到最后一个观察值，而目标方法则将预测结果与观察值索引对齐。method- 解析（默认），模拟或自举，表明预测方法。并非所有方法支持所有步数。simulations- 非负整数，方法为simulation或bootstrap时表明模拟次数。
1.3.4 预测结果解读
调用 forecast() 方法会返回 ARCHModelForecast 目标类，它具有3个核心属性和另外1个模拟预测或自举预测有用的属性。
三个属性为：
mean- 预测条件均值。variance- 预测条件方差。residual_variance- 预测残差的方差。当步数大于1的模型动态变化时，这与方差variance不同（比如AR模型）。
每一种属性包含一个共同的DataFrame结构。
print(forecasts.variance.tail()) h.1 h.2 h.3 h.4 h.5
Date
2013-12-24 0.489534 0.495875 0.501122 0.509194 0.518614
2013-12-26 0.474691 0.480416 0.483664 0.491932 0.502419
2013-12-27 0.447054 0.454875 0.462167 0.467515 0.475632
2013-12-30 0.421528 0.430024 0.439856 0.448282 0.457368
2013-12-31 0.407544 0.415616 0.422848 0.430246 0.439451h.1列中的值表示一步预测结果，其他h.2,...,h.5分别表示再往前2，...,5列的预测结果。表示结果时日期列是最后使用数据日期进行预测的时间，因而h.1 在行 2013-12-31 是指使用包括2013年12月31日的数据提前一步预测的结果。
默认预测则仅在最后观察值之后对模型进行估计。
day = dt.timedelta(1)
print(forecasts.variance[split_date - 5 * day:split_date + 5 * day])返回值如下：
h.1 h.2 h.3 h.4 h.5
Date
2009-12-28 NaN NaN NaN NaN NaN
2009-12-29 NaN NaN NaN NaN NaN
2009-12-30 NaN NaN NaN NaN NaN
2009-12-31 NaN NaN NaN NaN NaN
2010-01-04 0.739303 0.741100 0.744529 0.746940 0.752688
2010-01-05 0.695349 0.702488 0.706812 0.713342 0.721629
2010-01-06 0.649343 0.654048 0.664055 0.672742 0.681263结果总与数据输入行相同；无预测值由nan填充（注：即空值）.
1.3.5 结果类
class arch.univariate.base.ARCHModelForecast(index, mean, variance, residual_variance, simulated_paths=None, simulated_variances=None, simulated_residual_variances=None, simulated_residuals=None, align='origin')[source]
基于ARCH模型的预测容器。
| Parameters: |
|
|---|
mean
DataFrame – 过程条件均值的预测值
variance
DataFrame – 过程条件方差的预测值
residual_variance
DataFrame – 残差的条件方差的预测值
classarch.univariate.base.ARCHModelForecastSimulation(values, residuals, variances, residual_variances)[source]
基于ARCH模型的模拟或自举预测容器
| Parameters: |
|
|---|
values
DataFrame – 过程模拟值
residuals
DataFrame – 产生值的模拟残差
variances
DataFrame – 模拟值方差
residual_variances
DataFrame – 模拟残差的方差