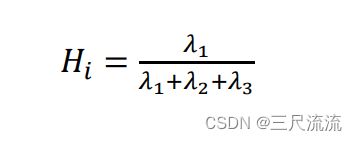点云凹凸性检验(2/2)
凹凸性
当我们持有表面点云数据时。可能从某个方向看向数据,此区域是凹陷的,但是当我们从背向看过来时其又是凸起的。这使得我们产生一个误会:在判断点云的凹凸性之前,是否需要先规定一下点云的表侧和里侧?
事实上在大多数情况下,我们仅仅需要。通过凹凸性检验的方法,将大面积的点云进行语义分割而已,如果这一半数据不是我想要的凹面或凸面,只需要抽取另一半的数据就好了。
凹凸性检验
逻辑
单个点云凹凸性逻辑如下图:
当P1点的曲率大小达到一定的阈值时,我们希望知道此处点云的凹凸性。
考虑到此逻辑计算的复杂程度,在处理之前先缩小一下待处理点的范围,仅曲率较大的点做凹凸性的判断。
曲率的公式如下:
一般认为是协方差的最小特征值/其他特征值之和
流程
1.通过最小生成树估计的我们可以获得P1点的法向量V1,逻辑图中可以看出这个曲面是凹陷的。
2.P1点通过open3d的k临近查找,可以获得最近三个点的坐标索引。使用此三点构建空间平面。
3.使用P1点对该平面进行投影,而投影点和原点P1可构成另一检测向量V2。
4.计算V1,V2夹角,一般认为夹角小于90度的就可以视为凹陷面了,反之为凸面。
完整代码
注意,以下代码的执行步骤是先执行“1.抽取曲率范围”和“2.法向量估计”。将这两步输出数据的地址分别填入“3.检测向量与计算”的data_cur和data_vec就可以执行“3.检测向量与计算”了
1.抽取曲率范围
import open3d as o3d
import numpy as np
import os
def pca_compute(data, sort=True):
"""
点云的特征值与特征向量
:return: 特征值与特征向量
"""
average_data = np.mean(data, axis=0)
decentration_matrix = data - average_data
H = np.dot(decentration_matrix.T, decentration_matrix)
eigenvectors, eigenvalues, eigenvectors_T = np.linalg.svd(H)
if sort:
sort = eigenvalues.argsort()[::-1]
eigenvalues = eigenvalues[sort]
return eigenvalues
def caculate_surface_curvature(radius,pcd):
"""
计算点云的表面曲率
:return: 点云中每个点的表面曲率
"""
cloud = pcd
points = np.asarray(cloud.points)
kdtree = o3d.geometry.KDTreeFlann(cloud)
num_points = len(cloud.points)
curvature = [] # 储存表面曲率
for i in range(num_points):
k, idx, _ = kdtree.search_radius_vector_3d(cloud.points[i], radius)
neighbors = points[idx, :]
w = pca_compute(neighbors)
delt = np.divide(w[2], np.sum(w), out=np.zeros_like(w[2]), where=np.sum(w) != 0)
curvature.append(delt)
curvature = np.array(curvature, dtype=np.float64)
return curvature
def curvature_normal():
'''
传入的曲率curvature归一化,传出诡异数据到绘图模块
:return:
'''
data_normal = caculate_surface_curvature(radius,pcd)
ave = np.mean(data_normal)
data_max = max(data_normal)
data_min = min(data_normal)
cur_normal = [(float(i) - data_min) / (data_max - data_min) for i in data_normal]
return cur_normal
def draw(cur_max,cur_min,pcd):
'''
绘图法向量绘图,曲率可视化绘图
:return:
'''
cur_normal = curvature_normal()
downpcd_normals = pcd
print(pcd)
print(cur_normal)
pcd.paint_uniform_color([0.5,0.5,0.5])
for i in range(len(cur_normal)):
if 0 < cur_normal[i] <= cur_min:
np.asarray(pcd.colors)[i] = [1, 0, 0]
elif cur_min < cur_normal[i] <= cur_max:
np.asarray(pcd.colors)[i] = [0, 1, 0]
elif cur_max < cur_normal[i] <= 1:
np.asarray(pcd.colors)[i] = [0, 0, 1]
# 曲率分割基准
o3d.visualization.draw_geometries([downpcd_normals],window_name="可视化原始点云",
width=800, height=800, left=50, top=50,
mesh_show_back_face=False)
return None
def save_txt1(cur_min,filename):
'''
存1列txt
:return:
'''
un1 = []
cur_normal = curvature_normal()
for i in range(len(cur_normal)):
if cur_normal[i] > cur_min:
un1.append(i)
savefilename = "%s"%(filename) + ".txt"
savefilename = "D:/db/txt/" + savefilename
if not os.path.exists(savefilename):
f = open(savefilename, 'w')
f.close()
with open(savefilename, 'w') as file_to_write:
for i in range(len(un1)):
file_to_write.writelines(str(un1[i]) + "\n")
return None
if __name__ == '__main__':
cur_max = 0.7
cur_min = 0.4
radius = 0.07
pcd = o3d.io.read_point_cloud("D:/db/bunny_pcd.pcd")
caculate_surface_curvature(radius,pcd)
print(caculate_surface_curvature(radius,pcd))
curvature_normal()
draw(cur_max,cur_min,pcd)
filename = "data_cur"
# 使用此函数记得更改文件名!!!!!!!!
save_txt1(cur_min,filename)图中蓝绿色点部分为曲率大于0.4的部分区域,而蓝色部分为曲率大于0.7的区域 。现抽取的点为大于0.4的点。
2.法向量估计
import open3d as o3d
import numpy as np
import os
pcd = o3d.io.read_point_cloud("D:/db/bunny_pcd.pcd")
pcd.paint_uniform_color([1.0, 0.0, 0.0])
pcd.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=0.01, max_nn=30)) #
pcd.orient_normals_consistent_tangent_plane(8)
print(np.asarray(pcd.normals)[:10, :])
def save_txt3(xlist,ylist,zlist,filename):
'''
存3列txt
:return:
'''
savefilename = "%s"%(filename) + ".txt"
savefilename = "D:/db/txt/" + savefilename
if not os.path.exists(savefilename):
f = open(savefilename, 'w')
f.close()
with open(savefilename, 'w') as file_to_write:
for i in range(len(xlist)):
file_to_write.writelines(str(xlist[i]) + " " + str(ylist[i]) + " " + str(zlist[i]) + "\n")
return None
xlist = []
ylist = []
zlist = []
for i in range(len(pcd.points)):
xlist.append(np.asarray(pcd.normals)[i][0])
ylist.append(np.asarray(pcd.normals)[i][1])
zlist.append(np.asarray(pcd.normals)[i][2])
filename = "data_vec"
# 使用此函数记得更改文件名!!!!!!!!
save_txt3(xlist,ylist,zlist,filename)
o3d.visualization.draw_geometries([pcd], point_show_normal=True, window_name="朝向相机位置",
width=1024, height=768,
left=50, top=50,
mesh_show_back_face=False) # 可视化点云和法线
3.检测向量与计算
import open3d as o3d
import numpy as np
import matplotlib.pyplot as plt
def project(data_cur,pcd):
'''
计算检测向量
:return:
'''
vector_list = []
pcd_tree = o3d.geometry.KDTreeFlann(pcd)
for i in data_cur:
# 由原点查找临近的三点
k, idx, _ = pcd_tree.search_knn_vector_3d(pcd.points[int(i)], 3)
# 原点
x, y, z = pcd.points[idx[0]]
# 平面点
x1, y1, z1 = pcd.points[idx[0]]
x2, y2, z2 = pcd.points[idx[1]]
x3, y3, z3 = pcd.points[idx[2]]
# 平面方程
A = y2 * z3 - y2 * z1 - y1 * z3 - y3 * z2 + y1 * z2 + y3 * z1
B = x3 * z2 - x1 * z2 - x3 * z1 - x2 * z3 + x2 * z1 + x1 * z3
C = x2 * y3 - x2 * y1 - x1 * y3 - x3 * y2 + x3 * y1 + x1 * y2
D = x1 * y3 * z2 + x2 * y1 * z3 + x3 * y2 * z1 - x1 * y2 * z3 - x3 * y1 * z2 - x2 * y3 * z1
A, B, C, D = -A, -B, -C, -D
# 投影点
xp = ((B ** 2 + C ** 2) * x - A * (B * y + C * z + D)) / (A ** 2 + B ** 2 + C ** 2)
yp = ((A ** 2 + C ** 2) * y - B * (A * x + C * z + D)) / (A ** 2 + B ** 2 + C ** 2)
zp = ((A ** 2 + B ** 2) * z - C * (A * x + B * y + D)) / (A ** 2 + B ** 2 + C ** 2)
# 垂直向量
n_ver = [xp - x, yp - y, zp - z]
vector_list.append(n_ver)
return vector_list
def vectorial_angle(data_vec,vector_list,data_cur):
'''
计算检测向量和法向量夹角
:return:
'''
angle_recolist = []
for i in range(len(vector_list)):
a = np.array(vector_list[i])
b = np.array(data_vec[int(data_cur[i])])
a_norm = np.sqrt(np.sum(a * a))
b_norm = np.sqrt(np.sum(b * b))
cos_value = np.dot(a, b) / (a_norm * b_norm)
arc_value = np.arccos(cos_value)
angle_value = arc_value * 180 / np.pi
angle_recolist.append(angle_value)
return angle_recolist
def draw(pcd,data_cur,angle_recolist):
'''
描述凹凸点
:return:
'''
pcd.paint_uniform_color([0.5, 0.5, 0.5])
for i in range(len(data_cur)):
# 凸起
if angle_recolist[i] > 90:
np.asarray(pcd.colors)[int(data_cur[i])] = [1, 0, 0]
# 凹陷
else:
np.asarray(pcd.colors)[int(data_cur[i])] = [0, 0, 1]
o3d.visualization.draw_geometries([pcd], point_show_normal=True, window_name="朝向相机位置",
width=1024, height=768,
left=50, top=50,
mesh_show_back_face=False)
return None
def draw_plt(pcd,data_cur,angle_recolist):
fig1 = plt.figure()
ax1 = fig1.add_subplot(111, projection='3d')
ax1.set_xlabel("x")
ax1.set_ylabel("y")
ax1.set_zlabel("z")
x_global = []
y_global = []
z_global = []
for i in range(len(pcd.points)):
[x,y,z] = np.asarray(pcd.points[i])
x_global.append(x)
y_global.append(y)
z_global.append(z)
x_u = []
y_u = []
z_u = []
x_n = []
y_n = []
z_n = []
for i in range(len(data_cur)):
# 凸起
if angle_recolist[i] > 90:
x_n.append(np.asarray(pcd.points)[int(data_cur[i])][0])
y_n.append(np.asarray(pcd.points)[int(data_cur[i])][1])
z_n.append(np.asarray(pcd.points)[int(data_cur[i])][2])
# 凹陷
else:
x_u.append(np.asarray(pcd.points)[int(data_cur[i])][0])
y_u.append(np.asarray(pcd.points)[int(data_cur[i])][1])
z_u.append(np.asarray(pcd.points)[int(data_cur[i])][2])
ax1.scatter(x_global, y_global, z_global, c='y', marker='.')
ax1.scatter(x_u, y_u, z_u, c='b', marker='*')
ax1.scatter(x_n, y_n, z_n, c='r', marker='*')
plt.show()
return None
def read_txt1(file):
'''
读一列
:return:
'''
un1 = []
for line in file.readlines():
line = line.strip('\n')
data = [float(i) for i in line.split()]
un1.append(data[0])
return un1
def read_txt3(file):
data_vec = []
for line in file.readlines():
line = line.strip('\n')
data_vec.append([float(i) for i in line.split()])
return data_vec
if __name__ == '__main__':
pcd = o3d.io.read_point_cloud("D:/db/bunny_pcd.pcd")
data_cur = read_txt1(open("D:/db/txt/data_cur.txt", "r"))
data_vec = read_txt3(open("D:/db/txt/data_vec.txt", "r"))
vector_list = project(data_cur, pcd)
angle_recolist = vectorial_angle(data_vec, vector_list,data_cur)
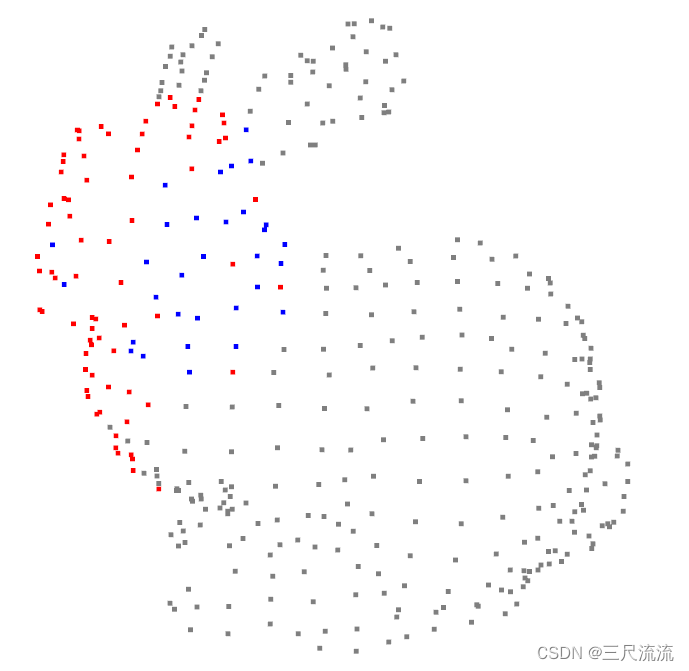
draw(pcd, data_cur, angle_recolist) 图中可以看到,兔子脖子和眼睛部分的凹陷已经基本表现,一些大范围的凹陷区域可能存在由于数据不均匀出现误判。用同样的方法对另一个密集的点云作处理,我们发现虽然凹陷与凸起的区域任然有少量的交错,但是还是在可以去噪处理的范围内。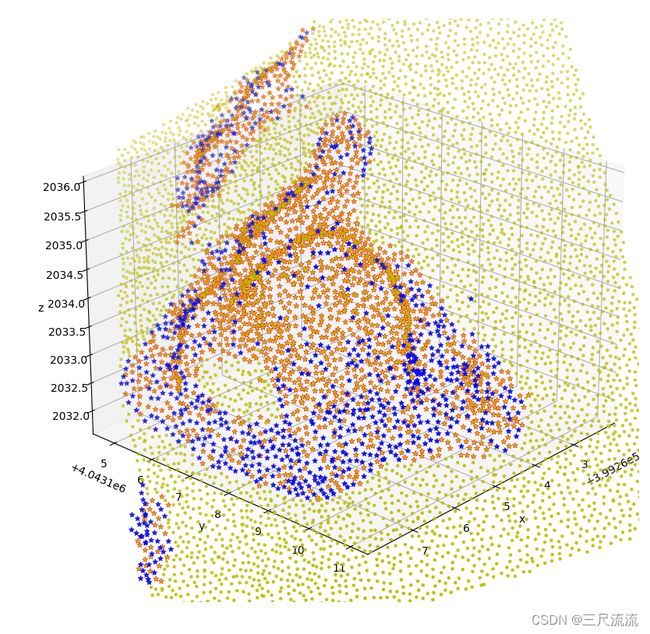
参考文献
【1】点云侠.Open3D 计算点云的表面曲率.