【论文悄悄递-GAIRAT】GEOMETRY-AWARE INSTANCE-REWEIGHTED ADVERSARIAL TRAINING
GEOMETRY-AWARE INSTANCE-REWEIGHTED ADVERSARIAL TRAINING
摘要
在对抗机器学习中,我们总是认为鲁棒性和准确性会互相抵触。这种观念被最近的一些研究所打破,我们可以维持鲁棒性并且提高准确率。然而,另一方面,我们可以维持准确性并且提高鲁棒性,这在概念上和实践上都很有趣,因为对于任何模型而言,鲁棒准确性应该是比标准准确性更低的。
本文中,我们展示了这个方向也是很有价值的:
- 首先,我们发现了过参数化的深层网络可能仍然有不能胜任的模型容量,因为对抗训练有压倒性的平滑影响(Q:过拟合?)
- 第二,鉴于受限的模型容量,我们建议对抗数据应该有不同的重要性:从几何上来说,一个自然数据点应该是距离分类边界越近越不健壮,越远越健壮,相应的对抗数据点应该是被分配给更大或更小的权重。
- 第三,为了实现这个想法,我们提出了GEOMETRY-AWARE INSTANCE-REWEIGHTED ADVER SARIAL TRAINING,其中权重是基于对于攻击一个自然数据点是多么困难决定的。
实验表明,该方法提高了标准对抗训练的鲁棒性;包括两个方向,我们可以提高标准对抗训练的准确性和鲁棒性这两者
引言
精心制作的对抗数据可以很容易地通过在自然数据中添加人类察觉不到的噪声来欺骗标准训练的深度模型,这导致了医疗、金融和自动驾驶等应用的安全问题。为了缓解这一问题,许多对抗训练方法采用最多的对抗数据最大化损失以更新当前模型,如标准对抗训练(AT) (PGD)、TRADES 、RST和MART等。 对抗训练方法寻求训练一个对抗鲁棒性深度模型,其预测对其输入的小邻域是局部不变的。(有 ϵ \epsilon ϵ的妥协空间)通过利用对抗性数据平滑小邻域,对抗训练方法获得对抗数据的对抗鲁棒性,但往往会导致自然数据标准精度的不良下降。
因此,关于稳健性和准确性之间是否存在权衡一直存在争论。
- 有些人认为有不可避免地权衡:
- Tsipras et al. (2019) 表明标准训练模型和对抗训练模型学习到的根本不同的表示。
- Zhang et al. (2019) and Wang et al. (2020a) 提出了对抗训练方法,可以权衡标准训练准确性来换取对抗训练鲁棒性。
- 另一方面,有些人认为没有这样的权衡:
- Raghunathan et al. (2020) s表明无限的数据可以消除这种trade-off,
- Yang et al.(2020) 表明基准图形数据集是类别分离的(??)
最近,新兴的对抗性训练方法从经验上挑战了这种trade-off。例如:
- Zhang et al. (2020b)提出了 friendly adversarial training方法(FAT),在发现一些错误预测的对抗数据的情况下,采用friendly adversarial data最小化损失。
- Yang et al.(2020)将dropout (Srivastava et al., 2014)引入了现有的ATRST和TRADES方法。
两种方法都能在保持鲁棒性的同时提高精度。然而,另一个方向——我们能否在保持准确性的同时提高鲁棒性——仍未解决,并且,更加令人感兴趣。
在本文中,我们表明这一方向也是可以实现的。
- 首先,由于对抗训练具有压倒性的平滑效果,过度参数化的深度网络可能仍然缺乏足够的模型容量。拟合对抗数据需要巨大的模型容量:它需要大量的可训练参数或足够长的训练周期,以在对抗训练数据上达到接近零的误差(见图2)。在标准训练中完全拟合自然数据的过参数化模型仍然远远不足以拟合对抗数据。与标准训练拟合自然数据点相比,对抗训练平滑了自然数据的邻域,使得对抗数据消耗的模型容量明显大于自然数据。因此,对抗训练方法应该谨慎地利用有限的模型能力来拟合重要数据的邻域,以帮助微调决策边界。 因此,对所有对立的数据给予同等的权重可能是不明智的。
- 其次,数据及其对抗变量并不同等重要。一些数据几何上远离分类边界。他们相对来说是被保护的(guarded)。它们的对抗变量很难被错误分类。另一方面,有些数据接近分类的边界。它们相对来说是容易被攻击的(attackable)。它们的对抗变量很容易被误分类(见图3)。随着对抗训练的进行,对抗鲁棒模型产生越来越多的guarded训练数据和越来越少的attackable训练数据。在模型容量有限的情况下,平等对待所有数据可能会导致大量guarded数据的对抗变量“淹没”模型,导致不希望的鲁棒过拟合(Rice et al., 2020)。因此,在对抗性训练中平等对待所有数据可能是很不好的。
为了改善这种情况,我们提出了一种启发式方法,即:GAIRAT。如图1所示,gaairat以不同的方式对待数据。特别地,为了更新当前的模型,GAIRAT对attackable/guarded数据点对抗变量的损失给予较大/较小的权重,这在微调决策边界时更重要/不重要。一个attackable/guarded数据点有一个小/大的几何距离(geometric distance),即它到决策边界的距离。我们使用PGD需要生成错误分类对抗变量的最小迭代数 κ \kappa κ来近似其几何距离(详见3.3节)。基于最小迭代数 κ \kappa κ, GAIRAT显式地将与实例相关的权重(instance dependent weight)分配给其对抗变量的损失值。
我们的贡献如下:
- 在对抗训练上,我们认为,由于模型容量不足和不同数据的不平等性质,在平等对待所有数据方面,我们不认同(见3.1节)。
- 我们提出了一个新的对抗训练方法GAIRAT(它的学习目标在3.2节,并且它的实现在3.3节)GAIRAT是一个通用的方法,除了standard AT(PGD),现存的对抗训练例如FAT和TRADES可以修改为GAIR-FAT和GAIR-TRADES(分别在附录B.1和B.2)
- 经验性地,我们的GAIRAT可以减轻鲁棒性过拟合问题,同时,改进后的鲁棒性在准确性上有着零或者很小的退化(参见4.1节和附录C.1)。
除此之外,我们使用ResNets来证实我们的GAIR方法的有效性:我们的GAIRAT很重要地增强了standard AT的鲁棒性;相比于FAT,我们的GAIR-FAT提高了鲁棒性和standard AT的准确性(4.2节)。因此,我们推测鲁棒性和准确性之间没有不可避免地权衡(Q,那TRADES呢,FAT是不是能提高准确性来着??)
对抗训练
在这一节,我们回顾了对抗训练方法PGD和FAT。
学习目标
设 ( X , d ∞ ) (\mathcal{X},d_\infty) (X,d∞)为无限距离度量 d inf ( x , x ′ ) = ∣ ∣ x = x ′ ∣ ∣ ∞ d_{\inf}(x,x')=||x=x'||_\infty dinf(x,x′)=∣∣x=x′∣∣∞的输入特征空间 X \mathcal{X} X,设 B ϵ [ x ] = { x ′ ∈ X ∣ d inf ≤ ϵ } \mathcal{B}_{\epsilon}[x]=\{x'\in\mathcal{X}|d_{\inf}\leq\epsilon\} Bϵ[x]={x′∈X∣dinf≤ϵ}以 ϵ > 0 \epsilon>0 ϵ>0为半径以在 X \mathcal{X} X空间中的 x x x为中心的闭球。数据集 S = { ( x i , y i ) } i = 1 n S=\{(x_i,y_i)\}^n_{i=1} S={(xi,yi)}i=1n,其中 x i ∈ X x_i\in\mathcal{X} xi∈X且 y i ∈ Y = { 0 , 1 , … , C − 1 } y_i\in\mathcal{Y}=\{0,1,\dots,C-1\} yi∈Y={0,1,…,C−1}。
-
standard adversarial training (AT)的目标函数是
min f θ ∈ F ∑ i = 1 n l ( f θ ( x ~ i ) , y i ) (1) \min_{f_\theta\in\mathcal{F}}\sum_{i=1}^{n}\mathcal{l}(f_{\theta}(\tilde{x}_{i}),y_{i})\tag{1} fθ∈Fmini=1∑nl(fθ(x~i),yi)(1)
其中:
x ~ i = arg max x ~ ∈ B ϵ [ x i ] l ( f θ ( x ~ ) , y i ) (2) \tilde{x}_i=\argmax_{\tilde{x}\in \mathcal{B}_{\epsilon}[x_i]}l(f_\theta(\tilde{x}),y_i)\tag{2} x~i=x~∈Bϵ[xi]argmaxl(fθ(x~),yi)(2)
其中 x ~ \tilde{x} x~是以x为中心的 ϵ \epsilon ϵ-ball中最多的对抗数据, f θ ( ⋅ ) : X → R C f_\theta(\cdot):\mathcal{X}\rightarrow\mathbb{R}^{C} fθ(⋅):X→RC是得分函数,损失函数 l : R C × Y → R l:\mathbb{R}^C\times\mathcal{Y}\rightarrow\mathbb{R} l:RC×Y→R是基本损失 l B : Δ C − 1 × Y → R C l_B:\Delta^{C-1}\times\mathcal{Y}\rightarrow\mathbb{R}^C lB:ΔC−1×Y→RC和反链接函数 l L : R C → Δ C − 1 l_L:\mathbb{R}^C\rightarrow\Delta^{C-1} lL:RC→ΔC−1的组合,其中 Δ C − 1 \Delta^{C-1} ΔC−1是相应的概率单纯形,换句话说 l ( f θ ( ⋅ ) , y ) = l B ( l L ( f θ ( ⋅ ) , y ) ) l(f_\theta(\cdot),y)=l_B(l_L(f_\theta(\cdot),y)) l(fθ(⋅),y)=lB(lL(fθ(⋅),y)),AT采用了根据Eq. (2)生成的最多的对抗数据来更新当前模型 -
friendly adversarial training (FAT) 的目标函数是
x ~ i = arg min x ~ ∈ B ϵ [ x i ] l ( f θ ( x ~ ) , y i ) s . t . l ( f θ ( x ~ ) , y i ) − min y ∈ Y l ( f θ ( x ~ ) , y ) ≥ ρ (3) \tilde{x}_i=\argmin\limits_{{\tilde{x}\in \mathcal{B}_{\epsilon}[x_i]}}l(f_\theta(\tilde{x}),y_i)s.t. l(f_\theta(\tilde{x}),y_i)-\min_{y\in\mathcal{Y}}l(f_{\theta}(\tilde{x}),y)\geq\rho \tag{3} x~i=x~∈Bϵ[xi]argminl(fθ(x~),yi)s.t.l(fθ(x~),yi)−y∈Yminl(fθ(x~),y)≥ρ(3)
注意:外部优化函数仍然与Eq. (1)相同, arg max \argmax argmax
被 arg min \argmin argmin取代, ρ \rho ρ是损失变量的边界值(即误分类置信度),Eq. (3)的约束首先确保了 x ~ \tilde{x} x~是被误分类的,其次在损失值方面,确保了对于 x ~ \tilde{x} x~错误预测比期望的预测 y i y_i yi至少好 ρ \rho ρ。在所有的满足约束条件的 x ~ \tilde{x} x~中,Eq.(3)通过违背变量 ρ \rho ρ选择了一个最小化 l ( f θ ( x ~ ) , y i ) l(f_\theta(\tilde{x}),y_i) l(fθ(x~),yi)。如果 x ~ i \tilde{x}_i x~i被正确分类,那么对 x ~ i \tilde{x}_i x~i就没有约束。FAT采用了根据Eq.(3)生成的friendly adversarial data来更新当前模型
实现
AT 和 FAT 的目标函数意味着对抗鲁棒网络的优化,一步生成对抗数据,一步最小化关于模型参数 θ \theta θ 的被生成的对抗数据的损失。
PGD是搜索对抗数据最常用的近似方法,在给定起始点 x ( 0 ) ∈ X x^{(0)\in\mathcal{X}} x(0)∈X和步长 α > 0 \alpha>0 α>0的情况下,PGD按照如下公式进行
x ( t + 1 ) = Π B [ x ( 0 ) ] ( x ( t ) + α s i g n ( ∇ x ( t ) l ( f θ ( x ( t ) ) , y ) ) ) , t ∈ N x^{(t+1)}=\Pi_{\mathcal{B}[x^{(0)}]}(x^{(t)}+ \alpha sign(\nabla_{x^{(t)}}l(f_\theta(x^{(t)}),y))),t\in\mathbb{N} x(t+1)=ΠB[x(0)](x(t)+αsign(∇x(t)l(fθ(x(t)),y))),t∈N
直到一个确定的停止标准被满足。 l l l是损失函数; x ( 0 ) x^{(0)} x(0)指代自然数据或者被一个小的高斯或均匀随机噪声所扰动的阻燃数据;y是自然数据相应的标签; x ( t ) x^{(t)} x(t)是第 t t t步的对抗数据; Π B [ x ( 0 ) ] ( ⋅ ) \Pi_{\mathcal{B}[x^{(0)}]}(\cdot) ΠB[x(0)](⋅)是投影函数,如果必要的话,把对抗数据投影回 x ( 0 ) x^{(0)} x(0)为中心的 ϵ \epsilon ϵ-ball上
AT和FAT有不同的停止标准,AT采用了固定迭代次数 K K K,也叫做PGD- K K K算法,它被普遍运用在很多对抗训练方法中,例如CAT、DAT、TRADES和MART。另一方面,FAT采用了错误分类感知标准,例如, Zhang et al. (2020b)提出提前停止的PGD- K K K- τ \tau τ算法( τ ≤ K \tau\leq K τ≤K; K K K是固定的,并且是允许的最大迭代次数)一旦PGD- K K K- τ \tau τ发现当前模型错误分类了对抗数据,它就立即停止迭代( τ = 0 \tau=0 τ=0)或者再走几步( τ > 0 \tau>0 τ>0)。这种错误分类感知标准用于新兴的对抗训练方法,例如 MMA、FAT、ATES和Customized AT
AT 可以增强对对抗数据的鲁棒性,但不幸的是,它会显着降低自然数据的标准精度。 另一方面,FAT 具有更好的标准精度,鲁棒性几乎为零或几乎没有下降。
尽管如此,AT 和 FAT 更新模型参数时,都平等对待生成的对抗数据,这是没有必要的,有时甚至是悲观的。 在接下来的部分中,我们将介绍我们的方法 GAIRAT,它与现有方法(例如 AT、FAT 和 TRADES)兼容。 因此,GAIRAT 可以显着增强鲁棒性,而标准训练的精度几乎没有下降甚至为零下降。
GAIRAT
在本节中,我们提出了几何感知实例重加权对抗训练(GAIRAT)及其学习目标及其算法实现。
GAIRAT的动机
在标准训练中,过参数化网络ResNet-18,甚至ResNet-50有着足够的模型能力,这可以很容易完全拟合自然训练数据。然而,图2的左半部分表明,那些过参数化网络的模型能力是不足以拟合对抗数据的,在100个epoch的计算预算下,网络很难在对抗训练数据上达到0误差。此外,随着模型参数的显着增加,对抗训练误差仅减少一个小的常数因子。更糟糕的是,稍大的扰动界限 ϵ t r a i n \epsilon_{train} ϵtrain 显著地揭示了模型能力的这种不足(图2 右半部分):对抗训练误差随着 ϵ t r a i n \epsilon_{train} ϵtrain稍大而显著增加。令人惊讶的是,在 ϵ t r a i n = 16 / 255 \epsilon_{train} = 16/255 ϵtrain=16/255 时,自然数据的标准训练误差几乎为零。
对抗训练方法使用对抗数据来降低模型输出关于自然数据的微小变化的敏感性。在训练过程中,对抗数据是动态生成的,并根据当前模型进行自适应更改,以平滑自然数据的局部邻域。即使 ϵ t r a i n \epsilon_{train} ϵtrain很小,这个周围的体积关于输入维度 ∣ X ∣ |\mathcal{X}| ∣X∣也是指数级 ( 1 + ϵ t r a i n ) (1+\epsilon_{train}) (1+ϵtrain)的大小。因此,这种平滑度消耗了大量的模型容量。 在对抗训练中,我们应该通过拟合重要数据和忽略不重要的数据来谨慎地利用有限的模型容量。
更容易攻击/被保护的数据离类边界更近/更远我们可以通过数据对对抗攻击的鲁棒性来衡量数据的重要性。图 3 显示数据的鲁棒性(更易攻击或更受保护)与其与决策边界的几何距离密切相关。 从几何的角度来看,更多可攻击的数据更接近分类边界,其对抗变量对于微调决策边界以增强鲁棒性来说,更加重要。
GAIRAT 的学习目标
令 ω ( x , y ) \omega(x,y) ω(x,y)为对抗变量 x ~ \tilde{x} x~损失的几何感知权重分配函数,生成 x ~ \tilde{x} x~的内部优化仍然是遵循Eq. (2) 或者Eq. (3),外部最小化函数时:
min f θ ∈ F 1 n ∑ i = 1 n ω ( x i , y i ) l ( f θ ( x ~ i ) , y i ) (5) \min\limits_{f_\theta\in\mathcal{F}}\frac{1}{n}\sum_{i=1}^{n}\omega(x_{i},y_{i})\mathcal{l}(f_{\theta}(\tilde{x}_{i}),y_{i})\tag{5} fθ∈Fminn1i=1∑nω(xi,yi)l(fθ(x~i),yi)(5)
约束首先确保 y i = arg max i f θ ( x i ) y_{i}=\argmax_{i}f_{\theta}(x_i) yi=iargmaxfθ(xi)并且,其次确保 ω ( x i , y i ) \omega(x_i,y_i) ω(xi,yi)是一个关于几何距离(数据点 x i x_i xi到决策边界的距离)的非增函数,其中, ω ( x i , y i ) ≥ 0 \omega(x_i,y_i)\geq0 ω(xi,yi)≥0且 1 n ∑ i = 1 n ω ( x i , y i ) = 1 \frac{1}{n}\sum^{n}_{i=1}\omega(x_i,y_i)=1 n1∑i=1nω(xi,yi)=1
当 y i ≠ arg max i f θ ( x i ) y_{i}\neq\argmax_{i}f_{\theta}(x_i) yi=iargmaxfθ(xi)接没有约束,对于那些离决策边界很远的 x x x,我们可以舍弃他们(离群值),对于那些接近决策边界的 x,我们可以给它们分配很大的权重。本文中,我们不考虑离群值,因此,我们为对抗数据的损失值分配了很大权重,其对应了自然数据(?)被错误分类,下图是GAIRAT学习目标的图解
可以引入一个burn-in period,即,在训练的开始阶段, ω ( x i , y i ) = 1 \omega(x_i,y_i)=1 ω(xi,yi)=1,与输入 ( x i , y i ) (x_i,y_i) (xi,yi)的几何距离无关,因为当分类器没有正确学习时,几何距离最初的信息量较少。
GAIRAT的实现
Eq. (5)的学习目标表明,对抗鲁棒性网络的最优化,第一步是生成对抗数据,然后根据对应的自然数据的几何距离对它们重新加权损失值。第二步是最小化再赋权值的模型参数 θ \theta θ的损失函数
我们通过最小的迭代次数 κ ( x , y ) \kappa(x,y) κ(x,y)(PGD方法需要生成对抗变量 x ~ \tilde{x} x~来欺骗现在的网络,在给定了最大允许的迭代次数K和迭代步长 α \alpha α)来近似数据点 ( x , y ) (x,y) (x,y)的几何距离,因此,几何距离被近似为 κ \kappa κ(准确点应该是 κ × α \kappa\times\alpha κ×α),所以权重函数 ω \omega ω的值应该是关于 κ \kappa κ的非增的,我们把 κ ( x , y ) \kappa(x,y) κ(x,y)命名为数据 ( x , y ) (x,y) (x,y)的几何值。
如何计算最佳的 ω \omega ω仍然是一个开放性问题,因此,我们启发性地设计了不同的非增函数 ω \omega ω,我们在这给了一个例子,并且在附录C.3和4.1节讨论了更多例子
ω ( x , y ) = ( 1 + tanh ( λ ) + 5 × ( 1 − 2 × κ ( x , y ) / K ) ) 2 \omega(x,y)=\frac{(1+\tanh(\lambda)+5\times(1-2\times\kappa(x,y)/K))}{2} ω(x,y)=2(1+tanh(λ)+5×(1−2×κ(x,y)/K))
其中 κ / K ∈ [ 0 , 1 ] , K ∈ N + \kappa/K\in[0,1],K\in\mathbb{N}^{+} κ/K∈[0,1],K∈N+,且 λ ∈ R \lambda\in\mathbb{R} λ∈R如果 λ = + ∞ \lambda =+\infty λ=+∞,也就对于所有的对抗数据赋予了相等权重,GAIRAT涵盖了标准对抗训练(PGD)
算法1 是几何感知的PGD方法(GA-PGD),这个算法返回了最多的对抗数据和自然数据(?)的几何值
算法2 是GAIRAT,GAIRAT利用算法1获得对抗数据和几何值。对于每个minibatch,GAIRAT再分配了对抗数据 ( x ~ i , y i ) (\tilde{x}_i,y_i) (x~i,yi)关于他们相应的natural counterparts ( ~ x i , y i ) \tilde(x_i,y_i) (~xi,yi)的损失值,然后更新模型参数,最小化再分配权值的和。
GAIRAT是一个普遍模型,事实上FAT和TRADES可以被GAIRFAT和GAIRTRADES所改进

实验
本节,我们经验性地证明GAIRAT的有效性,4.1节表明GAIRAT可以减轻minimax-based对抗训练的不良鲁棒过拟合。值得注意的是,一些同时进行的研究提供了各种对抗训练策略,这也可以缓解鲁棒过拟合的问题。 在第 4.2 节中,我们使用 Wide ResNets 对 GAIRAT 和 GAIR-FAT 进行基准测试,并将它们与 AT 和 FAT 进行比较
在我们的实验中,我们考虑 ∣ ∣ x ~ − x ∣ ∣ ∞ ≤ ϵ ||\tilde{x}-x||_\infty\leq\epsilon ∣∣x~−x∣∣∞≤ϵ在训练和评估中有相同的 ϵ \epsilon ϵCIFAR-10和SVHN的所有图片都被正则化到 [ 0 , 1 ] [0,1] [0,1]。
GAIRAT减轻对抗过拟合
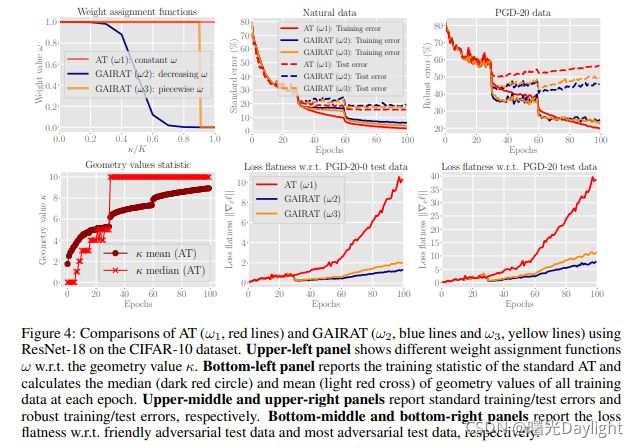
在图 4 中,
- 我们在 CIFAR 10 数据集上使用 ResNet-18执行标准 AT(all red lines)。 为了生成用于更新模型的最具对抗性的数据,扰动界限 ϵ = 8 / 255 \epsilon= 8/255 ϵ=8/255; PGD 步数 K = 10 K = 10 K=10,步长 α = 2 / 255 \alpha= 2/255 α=2/255,与 Rice et al. (2020)保持相同。
- 我们使用 SGD 训练 ResNet-18,动量(momentum)为 0.9,持续 100 个 epoch,初始学习率为 0.1,分别在 Epoch 30 和 60 时除以 10。 在每个训练时期,我们收集训练统计数据,即每个训练数据的几何值 κ ( x , y ) κ(x, y) κ(x,y)、标准/稳健训练和测试误差、关于对抗性测试数据的损失的平坦度 。
这些统计数据和评估的详细说明在附录 C.1 中。
图 4左下角为标准AT训练数据的几何值 κ κ κ。在训练过程中,当学习率在Epoch 30下降到0.01时,guarded训练数据的数量会突然增加。在Epoch 30之后,该模型稳步产生越来越多的guarded数据,这些数据的对抗变量被正确分类。从正确分类的对抗数据(大部分)中学习,可以强化已有的知识,而对错误预测的对抗数据(小部分)的关注较少,从而导致鲁棒过拟合。鲁棒过拟合表现在中上和右上以及中下和右下面板中的红色(虚线和实线)线
为了避免大量的保护数据压倒了从罕见的可攻击数据中学习的能力,我们的GAIRAT明确地对保护数据的对抗性变体的损失给予很小的权重。
左上角面板上的蓝色(ω2)和黄色(ω3)线给出了两种类型的权重分配函数,它们根据几何值κ为损失分配与实例相关的权重。在GAIRAT中,模型被迫对那些罕见的可攻击数据给予足够的关注
在GAIRAT中,最初的30个Epoch是老化期,我们从Epoch 31开始引入依赖于实例的权值分配ω(图4中的蓝黄线)。其余超参数保持与AT相同(红线)。从右上方的面板来看,与标准AT(红线)相比,GAIRAT(黄线和蓝线)在对抗测试数据上的误差更小,在训练对抗数据上的误差更大。因此,我们的GAIRAT可以缓解鲁棒过拟合的问题。
此外,附录C包含了更多的实验,如不同的学习速率计划,不同的权值分配函数ω的选择,不同的老化周期长度,不同的数据集(SVHN)和不同的网络(Small CNN和VGG),这些都证明了我们的有效性
GAIRAT。值得注意的是,在附录C.6中,我们展示了GAIR-FAT对改善FAT的效果。
WIDE RESNETS性能评价
结论和展望
本文提出了一种新的对抗训练方法,即GAIRAT。GAIRAT给对抗数据的损失更多(更少)权重,这些数据的自然对应物更接近(远离)决策边界。在有限的模型能力和固有的数据不平等的情况下,GAIRAT为改进对抗性训练提供了新的思路。
在PGD攻击下的gaairat训练可以很好地防御PGD攻击,但实际上,它并不能对所有现有的攻击都有同样好的表现(Chen et al., 2021a)。从哲学的角度来看,我们不能期望在某一特定攻击下的防御能够防御所有现有的攻击,这与之前的发现相呼应,即“由于防御训练是非适应性的,因此必须包括所有已知攻击产生的对抗性数据(Papernot et al., 2016)。在GAIRAT中合并所有攻击,但保持效率是一个有趣的未来方向。此外,如何设计Eq. 5中最优权值分配函数ω或设计适合对抗训练的网络结构仍然是一个悬而未决的问题。此外,将对抗性训练技术应用到其他领域仍有很大的空间,如预训练(Hendrycks等,2019;Chen et al., 2020;Jiang et al., 2020;Salman et al., 2020),噪声标签(Zhu et al., 2021)等。