决策树算法（实战篇——基于 sklearn 库）

决策树算法（实战篇——基于 sklearn 库）

  书接上回：决策树算法（原理篇），上节已经讲解了决策树算法的原理，本文则主要聚焦于 sklearn 决策树算法的实现。

一、sklearn 库对决策树算法实现的简介

1、sklearn 中的分类树

class sklearn.tree.DecisionTreeClassifier(criterion='gini', splitter='best', max_depth=None, min_samples_split=2,
											min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, 
											random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, 
											min_impurity_split=None, class_weight=None, presort=False)

2、sklearn 中的回归树

class sklearn.tree.DecisionTreeRegressor(criterion='squared_error', splitter='best', max_depth=None,
										min_samples_split=2,min_samples_leaf=1_, min_weight_fraction_leaf=0.0, 
										max_features=None,random_state=None, max_leaf_nodes=None, 
										min_impurity_decrease=0.0, ccp_alpha=0.0)

3、sklearn 中没有实现对 ID3 和 C4.5 算法的实现，对决策树算法的实现是基于 CART 算法，即生成的树是二叉树。但 sklearn.tree.DecisionTreeClassifier() 函数提供了更改特征选择标准的接口 criterion{“gini”, “entropy”}, default=“gini”，默认是基尼指数，也可更改为 ID3 使用的 “entropy”。

4、sklearn 中决策树算法也没实现对缺失数据的自动处理，故在使用前需确保自己的数据没有缺失值或缺失值已经过处理。

二、分类树实战

  目标：实现鸢尾属植物数据集分类。

from sklearn import tree
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

iris = load_iris()  # 加载数据集
print('feature_names: ', iris.feature_names)  # 打印特征名称
print('target_names: ', iris.target_names)  # 打印标签名称

X = iris.data
y = iris.target
print('X_0: ', X[0])
print('y_0: ', y[0])

# 将数据集划分为训练集和测试集，7:3
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y )

# 训练
clf = tree.DecisionTreeClassifier(criterion="entropy")  # 特征选择标准采用交叉熵
clf.fit(X_train, y_train)

# 测试
score = clf.score(X_test,y_test)
print('预测准确率：',score)

  输出：

feature_names: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] 
target_names: ['setosa' 'versicolor' 'virginica'] 
X_0: [5.1 3.5 1.4 0.2] 
y_0: 0 
预测准确率： 0.9777777777777777

  可以看到，测试集的准确接近 98%，接下来对生成的树进行可视化，需要用到 graphviz 库，可通过 “pip install graphviz” 安装。

import graphviz

dot_data = tree.export_graphviz(clf, out_file=None,
                    feature_names=iris.feature_names,
                    class_names=iris.target_names,
                    filled=True, rounded=True,
                    special_characters=True)

graph = graphviz.Source(dot_data)  
graph

三、回归树实战

  目标：利用 california 房价数据集预测房价。

from sklearn.model_selection import cross_val_score
from sklearn.datasets import fetch_california_housing
import numpy as np
import matplotlib.pyplot as plt

# 利用california房价数据集来测试交叉检验
# 对于分类模型，交叉验证返回的是模型的精确度
# 对于回归模型，交叉验证默认返回的是R^2
# 可以改变scoring参数改变返回数据
# 一般使用MSE(均方误差)

california = fetch_california_housing()  # 加载数据集

print('data_shape: ', california['data'].shape)
print('target_shape: ', california['target'].shape)
print('data_0 ~ data2: ', california['data'][0:3])
print('target_0 ~ target_2: ', california['target'][0:3])

# 定义模型
dtr = DecisionTreeRegressor()

# 交叉检验会自动分割数据据，所以不需要人为对数据据进行划分
# cv 表示划分数据集的份数，推荐5或10
# r2 越接近1越好
r2_cv = cross_val_score(dtr, california['data'], california['target'], cv=10)

# 返回负的均方误差，均方误差越接近0越好
neg_MSE_cv = cross_val_score(dtr, california['data'], california['target'], cv=10, scoring='neg_mean_squared_error')

print('r2_cv: ', r2_cv)  # 打印r2(10折交叉验证，故生成10个)
print('neg_MSE_cv: ', neg_MSE_cv)  # 打印负的均方误差

print('r2_cv_mean: ', np.mean(r2_cv))  # 10折交叉验证取平均值作为结果
print('neg_MSE_mean: ', np.mean(neg_MSE_cv))

  输出：

data_shape: (20640, 8)
target_shape: (20640,)
data_0 ~ data2: [[ 8.32520000e+00 4.10000000e+01 6.98412698e+00 1.02380952e+00 3.22000000e+02 2.55555556e+00 3.78800000e+01 -1.22230000e+02] [ 8.30140000e+00 2.10000000e+01 6.23813708e+00 9.71880492e-01 2.40100000e+03 2.10984183e+00 3.78600000e+01 -1.22220000e+02] [ 7.25740000e+00 5.20000000e+01 8.28813559e+00 1.07344633e+00 4.96000000e+02 2.80225989e+00 3.78500000e+01 -1.22240000e+02]]
target_0 ~ target_2: [4.526 3.585 3.521]

r2_cv: [-0.33856374 0.27356733 0.53514167 0.33054576 0.52029086 0.27411381 -0.03091102 0.28441455 0.20582289 0.35759738] neg_MSE_cv: [-1.21526597 -0.78310321 -0.74828875 -0.50358131 -0.8321429 -0.83956725 -0.54551068 -1.01664815 -1.03341229 -0.53092105]
r2_cv_mean: 0.24120195084501414
neg_MSE_mean: -0.8048441545613372

四、剪枝

  通过可视化 california 房价数据集生成树发现生成的树太大，过拟合，造成 $R^2$ 相对较小（可视化的代码可参考上述鸢尾花的代码，生成的树太大，在可视化过程中要跑好久，生成的树太大，我就没贴图上来了，感兴趣的可以自己跑跑）

  对此，需要对生成的树进行剪枝，在决策树原理篇的时候提过，剪枝分为预剪枝和后剪枝，遗憾的是，sklearn 并不提供后剪枝的接口，准确的说是后剪枝只提供了代价复杂度（CCP）的接口，故本文主要讲解预剪枝。

  sklearn 中提供了多个预剪枝的参数，这里讲解三个常用的：max_depth，min_samples_leaf 和 min_samples_split。

1、max_depth
  限制树的最大深度，超过设定深度的树枝全部剪掉。

  这是用得最广泛的剪枝参数，在高维度低样本量时非常有效。决策树多生长一层，对样本量量的需求会增加一倍，所以限制树深度能够有效地限制过拟合，在集成算法中也非常实用。实际用时，建议从 max_depth=3 开始尝试，看看拟合的效果再决定是否增加设定深度。

2、min_samples_leaf
  限定一个结点在分支后的每个子结点都必须包含至少 min_samples_leaf 个训练样本，否则分支就不会发生，或者，分支会朝着满足每个子结点都包含min_samples_leaf 个样本的方向去发生。

  一般搭配 max_depth 使用，在回归树中有神奇的效果，可以让模型变得更加平滑。这个参数的数量设置得太小会引起过拟合，设置得太大就会阻止模型学习数据。一般来说，建议从 min_samples_leaf=5 开始使用。如果叶结点中含有的样本量变化很大，建议输入浮点数作为样本量的百分比来使用。同时，这个参数可以保证每个叶子的最小尺寸，可以在回归问题中避免低方差，过拟合的叶子结点出现。对于类别不多的分类问题，min_samples_leaf=1 通常就是最佳选择。

3、min_samples_split
  限定一个结点必须要包含至少 min_samples_split 个训练样本，这个结点才允许被分支，否则分支就不会发生。

4、实战演练
  还是针对 california 房价数据集，通过限制树的最大深度进行剪枝，来看看剪枝后的效果

r2_cv_list = []
neg_MSE_cv_list = []

# 预剪枝，max_depth从3~12
for i in range(3, 13):
    dtr = DecisionTreeRegressor(max_depth=i)

    r2_cv = cross_val_score(dtr, california['data'], california['target'], cv=10)  # 10折交叉验证

    neg_MSE_cv = cross_val_score(dtr, california['data'], california['target'], cv=10, scoring='neg_mean_squared_error')

    r2_cv_list.append(np.mean(r2_cv))  # 存储不同 max_depth 剪枝后的树的10折交叉验证的r2

    neg_MSE_cv_list.append(np.mean(neg_MSE_cv))  # 存储不同 max_depth 剪枝后的树的10折交叉验证的负均方误差


print('r2_cv_mean: ', r2_cv_list)
print('neg_MSE_mean: ', neg_MSE_cv_list)

# 对比不同 max_depth 的输出结果
X = [i for i in range(3, 13)]
figure, axes = plt.subplots(1,2, constrained_layout=True)

plt.subplot(121)
my_x_ticks = np.arange(3, 13, 1)
plt.xticks(my_x_ticks)
plt.scatter(X, r2_cv_list, s=20, edgecolor="black", c="darkorange")
plt.plot(X, r2_cv_list, color="cornflowerblue", label="R2", linewidth=2)
plt.xlabel("max_depth")
plt.ylabel("R2")

plt.subplot(122)
my_x_ticks = np.arange(3, 13, 1)
plt.xticks(my_x_ticks)
plt.scatter(X, neg_MSE_cv_list, s=20, edgecolor="black", c="darkorange")
plt.plot(X, neg_MSE_cv_list, color="cornflowerblue", label="R2", linewidth=2)
plt.xlabel("max_depth")
plt.ylabel("neg_MSE")

plt.show()

  输出：

r2_cv_mean: [0.362339872567896, 0.4085440823327452, 0.4264727212988957, 0.4457019235789167, 0.46701552642829985, 0.4454246567721009, 0.4295066167957328, 0.39542514771894643, 0.37977573026744, 0.3526782320575567]
neg_MSE_mean: [-0.6869873231477238, -0.6357391403629961, -0.6095087208003013, -0.5869503251549955, -0.570637012704774, -0.5971705432853479, -0.6150513269134269, -0.6467230806992063, -0.6620477419151787, -0.6830877676789215]

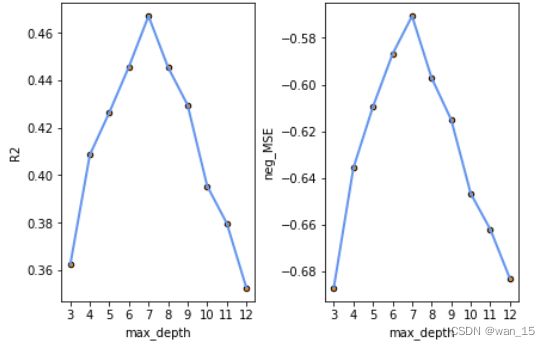
  由输出结果可得，当 max_depth=7 时性能最好，模型的 $R^2$ 相较未剪枝之前也有了提升，故选择剪枝参数为 max_depth=7，对全部数据集进行拟合，可视化：

import graphviz
from sklearn import tree

dtr = DecisionTreeRegressor(max_depth=7)  # 预剪枝max_depth=7
dtr = dtr.fit(california['data'], california['target'])
Y_pred = dtr.predict(california['data'])

dot_data = tree.export_graphviz(dtr, out_file=None,
                    feature_names=california.feature_names,  
                    class_names=california.target_names,  
                    filled=True, rounded=True,
                    special_characters=True)  

graph = graphviz.Source(dot_data)  
graph

  这里结果同样不贴图（生成的树还是相对较大，博客显示效果不好），感兴趣的可以自己跑跑，会发现程序运行的很快，生成的模型层数为7层，与原来没剪枝的相比减少了很多。

  这里只演示了 max_depth 对模型性能的影响，还有其它参数可调，当有多个参数需要调时，可使用网格搜索，寻找性能 “最佳” 的模型对应的参数，感兴趣的读者可自己动手实现下。

参考文献

---

# sklearn决策树之剪枝参数