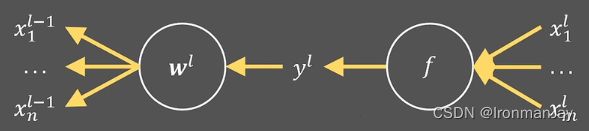Xavier参数初始化方法和Kaiming参数初始化方法详细介绍及其原理详解
相关文章
- 梯度下降算法、随机梯度下降算法、动量随机梯度下降算法、AdaGrad算法、RMSProp算法、Adam算法详细介绍及其原理详解
- 反向传播算法和计算图详细介绍及其原理详解
- 激活函数、Sigmoid激活函数、tanh激活函数、ReLU激活函数、Leaky ReLU激活函数、Parametric ReLU激活函数详细介绍及其原理详解
- Xavier参数初始化方法和Kaiming参数初始化方法详细介绍及其原理详解
文章目录
- 相关文章
- 前言
- 一、什么是参数初始化?
- 二、Xavier参数初始化方法
-
- 2.1 正态分布参数初始化
- 2.2 均匀分布参数初始化
- 2.3 Xavier参数初始化方法目标方差推导
- 三、Kaiming参数初始化方法
-
- 3.1 正态分布参数初始化
- 3.2 均匀分布参数初始化
- 3.3 Kaiming参数初始化方法目标方差推导
- 总结
前言
本文主要介绍了Xavier参数初始化方法和Kaiming参数初始化方法的基本概念以及公式原理性的推导过程,参数初始化的好坏直接关系到神经网络的训练结果,一个好的参数初始化方法,可以帮助我们避免梯度消失或者梯度爆炸的问题,所以对于参数初始化的学习也十分重要。下面就是本文的全部内容!
一、什么是参数初始化?
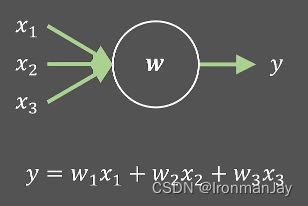
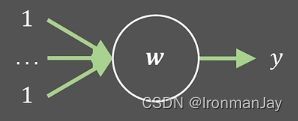
假设现在有一个神经元,其包含三个参数,分别为 w 1 , w 2 , w 3 w_{1},w_{2},w_{3} w1,w2,w3,这三个参数与三个输入数据 x 1 , x 2 , x 3 x_{1},x_{2},x_{3} x1,x2,x3经过线性运算 y = w 1 x 1 + w 2 x 2 + w 3 x 3 y=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3} y=w1x1+w2x2+w3x3得到输出 y y y,为了方便讨论,我们忽略截距 b b b,整个运算过程如下图所示:
很明显,我们需要给参数 w 1 , w 2 , w 3 w_{1},w_{2},w_{3} w1,w2,w3都赋予一个初始值才能进行运算,那么该如何选择 w 1 , w 2 , w 3 w_{1},w_{2},w_{3} w1,w2,w3的初始值使得神经网络的训练结果最好呢?当我们没有一个最优解的时候,可以试试最简单的方法,或许我们可以假设 w i = 0 ( 1 ≤ i ≤ 3 ) w_{i}=0(1≤i≤3) wi=0(1≤i≤3),确实,这样可以进行运算并训练,但是通过这样的赋值后进行训练有什么问题呢?
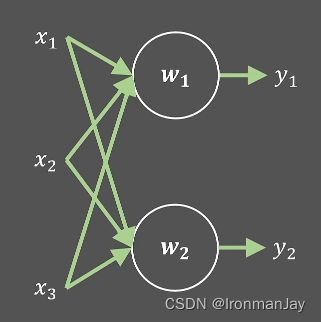
让我们基于刚刚的假设来看一个稍微复杂的情况,假如当前层的神经网络不止一个神经元,而是由两个神经元构成的,也就是如下图所示的结构:
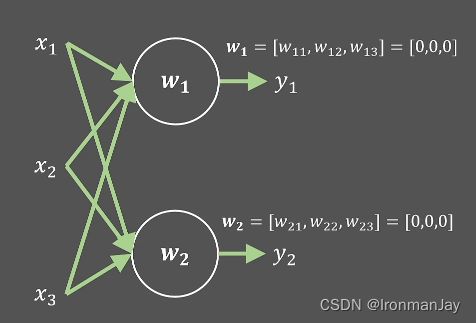
因为我们刚刚假设参数 w w w初始化为0,所以此时的 w i j = 0 ( 1 ≤ i ≤ 2 , 1 ≤ j ≤ 3 ) w_{ij}=0(1≤i≤2,1≤j≤3) wij=0(1≤i≤2,1≤j≤3):
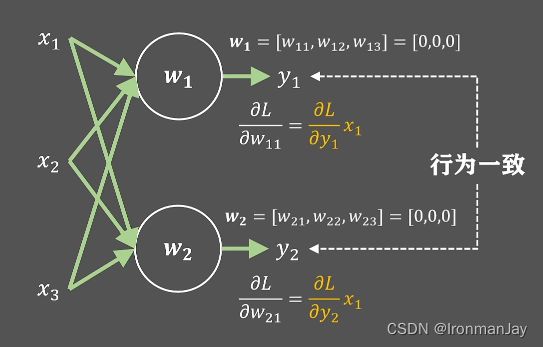
此时可以经过运算得到预测值 y 1 y_{1} y1和 y 2 y_{2} y2,根据之前学习的知识,我们要利用损失函数 L L L来更新参数 w w w,那么就要利用反向传播算法来最优化参数 w w w。另外,在此情况下, w w w的参数较多,我们以参数 w 11 w_{11} w11和 w 21 w_{21} w21为例。根据反向传播算法可以得到损失函数 L L L关于参数 w 11 w_{11} w11的梯度值:
∂ L ∂ w 11 = ∂ L ∂ y 1 x 1 \frac{\partial L}{\partial w_{11}}=\frac{\partial L}{\partial y_{1}} x_{1} ∂w11∂L=∂y1∂Lx1
同理,我们也可以计算损失函数 L L L关于参数 w 21 w_{21} w21的梯度值:
∂ L ∂ w 21 = ∂ L ∂ y 2 x 1 \frac{\partial L}{\partial w_{21}}=\frac{\partial L}{\partial y_{2}} x_{1} ∂w21∂L=∂y2∂Lx1
因为损失函数 L L L是关于参数 y y y的函数,所以:
∂ L ∂ y 1 ≡ ∂ L ∂ y 2 \frac{\partial L}{\partial y_{1}} \equiv \frac{\partial L}{\partial y_{2}} ∂y1∂L≡∂y2∂L
那么很明显,损失函数 L L L关于参数 w 11 w_{11} w11和 w 21 w_{21} w21的梯度值都是相等的:
∂ L ∂ w 11 ≡ ∂ L ∂ w 21 \frac{\partial L}{\partial w_{11}} \equiv \frac{\partial L}{\partial w_{21}} ∂w11∂L≡∂w21∂L
所以,如果我们将参数全部初始化为0,那么在训练过程中参数的变化就是一样的,也就意味着这一层的两个神经元状态会始终保持一致,没有办法学习和表达更复杂的特征,这种情况也被称为神经元的对称现象:
很明显,这种对称现象是我们需要避免的,既然参数全部初始化为0会导致对称现象,那么我们是不是可以在参数初始化的时候增加一点随机性呢?我们可以随机在服从独立正态分布 N ( 0 , 1 ) \mathcal{N}(0,1) N(0,1)的 w i w_{i} wi中选取 w 1 , w 2 , w 3 w_{1},w_{2},w_{3} w1,w2,w3来作为初始化的参数使用,如下图所示:
为了方便讨论,我们假设三个输入值都为1,代入到线性运算 y = w 1 x 1 + w 2 x 2 + w 3 x 3 y=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3} y=w1x1+w2x2+w3x3得到 y = w 1 + w 2 + w 3 y=w_{1}+w_{2}+w_{3} y=w1+w2+w3:
此时,我们计算一下输出 y y y的方差, Var ( y ) \operatorname{Var}(y) Var(y)其中需要注意的是, w 1 , w 2 , w 3 w_{1},w_{2},w_{3} w1,w2,w3是独立同分布于正态分布的参数,所以可以计算得到输出 y y y的方差 Var ( y ) \operatorname{Var}(y) Var(y):
Var ( y ) = Var ( w 1 ) + Var ( w 2 ) + Var ( w 3 ) = 3 \operatorname{Var}(y)=\operatorname{Var}\left(w_{1}\right)+\operatorname{Var}\left(w_{2}\right)+\operatorname{Var}\left(w_{3}\right)=3 Var(y)=Var(w1)+Var(w2)+Var(w3)=3
对其开根号就可以得到输出 y y y的标准差 Std ( y ) \operatorname{Std}(y) Std(y):
Std ( y ) = 3 = 1.732 \operatorname{Std}(y)=\sqrt{3}=1.732 Std(y)=3=1.732
此时输出 y y y的方差和标准差意味着输入 x 1 , x 2 , x 3 x_{1},x_{2},x_{3} x1,x2,x3经过神经元之后,输出 y y y的离散程度被提高了。
让我们考虑一种更通用的情况,上面讨论的是神经元只有3个输入的情况,那如果现在神经元不止三个输入,而是 n n n个输入,并且为了方便讨论,假设此 n n n个输入的输入值都为1。
此时可以注意到, y = ∑ i = 1 n w i y=\sum_{i=1}^{n} w_{i} y=∑i=1nwi,根据刚才的讨论,此时输出 y y y的方差 Var ( y ) \operatorname{Var}(y) Var(y)为:
Var ( y ) = n Var ( w i ) = n \operatorname{Var}(y)=n \operatorname{Var}\left(w_{i}\right)=n Var(y)=nVar(wi)=n
同样,对其开根号就可以得到输出 y y y的标准差 Std ( y ) \operatorname{Std}(y) Std(y):
Std ( y ) = n \operatorname{Std}(y)=\sqrt{n} Std(y)=n
可以看到,当神经元的输入越多时,输出 y y y的标准差 Std ( y ) \operatorname{Std}(y) Std(y)也就越大,这也就意味着其离散程度会被放大 n \sqrt{n} n倍。当我们得到输出 y y y后,又面临两种情况:
-
不使用任何激活函数
那么放大的 y y y值就会被累积在反向传播的过程中,这样就会造成梯度过大,从而导致梯度爆炸问题
-
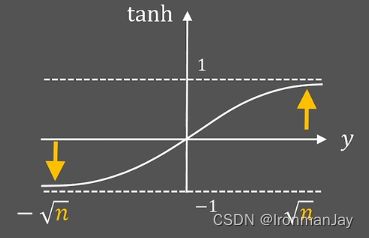
使用激活函数
比如利用双曲正切函数作为激活函数,那么就可能因为 y y y值的不稳定(过大或过小),而得到一个非常小的梯度,从而导致梯度消失问题
以上讨论的就是关于参数初始化的内容,可以看到,参数的初始化直接关系到神经网络模型训练的好坏,那么究竟该如何进行参数的初始化,使得神经网络模型的准确率或者是性能最佳呢?这也是下面我们要讨论的问题。
二、Xavier参数初始化方法
上面我们已经讨论过了,为了让神经网络训练过程稳定下来,那么我们需要选取合适的参数进行初始化,从而让 y y y的方差落在一个可控的范围内。仍以上面的讨论为例,假设有 n n n个输入都为1,经过线性运算后得到 y y y,这个过程如下图所示:
既然我们的目的是让 y y y的方差稳定,不妨在上面假设的情况中设 y y y最终的方差为1,此时 y y y的方差就在一个可控的范围内:
Var ( y ) = n Var ( w i ) = 1 \operatorname{Var}(y)=n \operatorname{Var}\left(w_{i}\right)=1 Var(y)=nVar(wi)=1
我们可以根据此式很容易的计算出参数 w i ( 1 ≤ i ≤ n ) w_{i}(1≤i≤n) wi(1≤i≤n)分布的方差:
Var ( w i ) = 1 n \operatorname{Var}\left(w_{i}\right)=\frac{1}{n} Var(wi)=n1
此时我们考虑一种更普遍的情况,也就是不仅考虑到输入的维度会对 y y y的方差造成影响,同时考虑到下一层神经元的数量,那么平均之后参数 w i w_{i} wi分布的方差为:
Var ( w i ) = 2 n in + n out \operatorname{Var}\left(w_{i}\right)=\frac{2}{n_{\text {in }}+n_{\text {out }}} Var(wi)=nin +nout 2
其中, n i n n_{in} nin为输入层神经元的数量, n o u t n_{out} nout为输出层神经元的数量。
2.1 正态分布参数初始化
现在我们已经知道了参数 w i w_{i} wi应该满足的方差,那么我们可以让参数 w i w_{i} wi在满足如下条件的正态分布中随机采样:
N ( 0 , 2 n in + n out ) \mathcal{N}\left(0, \frac{2}{n_{\text {in }}+n_{\text {out }}}\right) N(0,nin +nout 2)
此时我们就可以使输出 y y y的方差稳定,从而更好的训练模型,这种方法也被称为正态分布初始化。
2.2 均匀分布参数初始化
首先,让我们回顾一下均匀分布的相关基础知识:当 w i w_{i} wi满足从 a a a到 b b b的均匀分布 U ( a , b ) \mathcal{U}(\mathrm{a}, \mathrm{b}) U(a,b)时, w i w_{i} wi的期望 E ( w i ) E(w_{i}) E(wi)为:
E ( w i ) = ( a + b ) 2 E(w_{i})=\frac{(a+b)}{2} E(wi)=2(a+b)
所以, w i w_{i} wi的方差 Var ( w i ) \operatorname{Var}(w_{i}) Var(wi)为:
Var ( w i ) = E ( w i 2 ) − E ( w i ) 2 = ( b − a ) 2 12 \operatorname{Var}(w_{i})=E(w_{i}^{2})-E(w_{i})^{2}=\frac{(b-a)^{2}}{12} Var(wi)=E(wi2)−E(wi)2=12(b−a)2
当我们对均匀分布的基础知识有了了解之后,就容易做下面的工作了。因为我们需要保证采样的均值为零,所以我们可以取 w i w_{i} wi均匀分布的范围为 − a -a −a到 a a a,所以此时 w i w_{i} wi满足的均匀分布为 U ( − a , a ) \mathcal{U}(\mathrm{-a}, \mathrm{a}) U(−a,a)。那么此时代入公式得到 w i w_{i} wi的方差 Var ( w i ) \operatorname{Var}(w_{i}) Var(wi)为:
Var ( w i ) = a 2 3 \operatorname{Var}(w_{i})=\frac{a^{2}}{3} Var(wi)=3a2
刚刚我们分析过,参数 w i w_{i} wi的方差为 Var ( w i ) = 2 n in + n out \operatorname{Var}\left(w_{i}\right)=\frac{2}{n_{\text {in }}+n_{\text {out }}} Var(wi)=nin +nout 2时效果最好,所以可以得到:
Var ( w i ) = a 2 3 = 2 n in + n out \operatorname{Var}(w_{i})=\frac{a^{2}}{3}=\frac{2}{n_{\text {in }}+n_{\text {out }}} Var(wi)=3a2=nin +nout 2
那么代入数据反解得到参数 w i w_{i} wi应满足的均匀分布为:
U ( − 6 n in + n out , 6 n in + n out ) \mathcal{U}\left(-\sqrt{\frac{6}{n_{\text {in }}+n_{\text {out }}}}, \sqrt{\frac{6}{n_{\text {in }}+n_{\text {out }}}}\right) U(−nin +nout 6,nin +nout 6)
在实际应用中,正态分布初始化和均匀分布初始化都可以达到不错的效果,可以在一定程度上缓解梯度爆炸和梯度消失现象。这两种参数初始化方法就是2010年提出来的Xavier初始化方法。此种参数初始化的方法非常适合于双曲正切函数作为激活函数的情况。
2.3 Xavier参数初始化方法目标方差推导
上面只是对Xavier初始化方法做了一个简要的介绍,直接说明了其方差大小,但是这个方差是怎么得到的呢?这才是我们需要讨论的问题,可能有些难度,听我细细道来!首先,我们要有一些关于概率论与数理统计的基础知识储备:
-
公式一:
Var ( X ) = E ( X 2 ) − E ( X ) 2 \operatorname{Var}(X)=E\left(X^{2}\right)-E(X)^{2} Var(X)=E(X2)−E(X)2 -
公式二:
Var ( X + Y ) = Var ( X ) + Var ( Y ) \operatorname{Var}(X+Y)=\operatorname{Var}(X)+\operatorname{Var}(Y) Var(X+Y)=Var(X)+Var(Y) -
公式三:
Var ( X Y ) = Var ( X ) Var ( Y ) + Var ( X ) E ( Y ) 2 + Var ( Y ) E ( X ) 2 \operatorname{Var}(XY)=\operatorname{Var}(X)\operatorname{Var}(Y)+\operatorname{Var}(X)E(Y)^2+\operatorname{Var}(Y)E(X)^2 Var(XY)=Var(X)Var(Y)+Var(X)E(Y)2+Var(Y)E(X)2
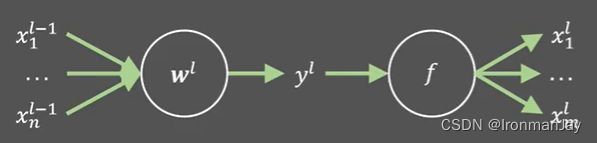
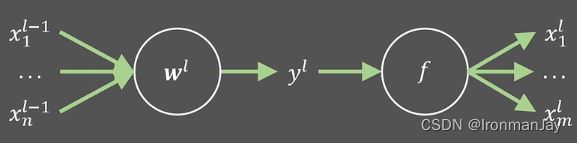
这三个公式是关于变量 X X X和 Y Y Y的期望和方差的相关计算,并且默认以上讨论的情况中和 Y Y Y相互独立,至于此公式怎么来的在此不赘述,默认读者有此方面基础(Ps:这部分内容并不是硬性要求一定需要看的)。现在考虑在正向传播中第 i i i层的神经元:
需要注意,我们忽略截距 b b b的影响,其中:
- 输入维度为 n n n
- 输出维度为 m m m
- 参数为 w w w向量
- 线性输出为 y y y
- 激活函数为 f f f
另外,为了方便讨论,我们做如下假设:
- 假设一: E ( x ) = 0 , E ( w ) = 0 E(x)=0,E(w)=0 E(x)=0,E(w)=0
- 假设二:激活函数 f f f对称,且${f}'(0)=1 $
- 假设三: x x x的方差都是相等的
有了以上基础概念和假设后,我们可以很明显的得到第 i i i层神经元的输出 y l y^{l} yl的值为:
y l = ∑ i = 1 n w i l x i l − 1 y^{l}=\sum_{i=1}^{n} w_{i}^{l} x_{i}^{l-1} yl=i=1∑nwilxil−1
由公式二可知, y l y^{l} yl的方差 Var ( y l ) \operatorname{Var}(y^{l}) Var(yl)为:
Var ( y l ) = ∑ i = 1 n Var ( w i l x i l − 1 ) = n Var ( w i l x i l − 1 ) \operatorname{Var}(y^{l})=\sum_{i=1}^{n} \operatorname{Var}(w_{i}^{l} x_{i}^{l-1})=n\operatorname{Var}(w_{i}^{l} x_{i}^{l-1}) Var(yl)=i=1∑nVar(wilxil−1)=nVar(wilxil−1)
让我们利用公式三,将 Var ( y l ) = n Var ( w i l x i l − 1 ) \operatorname{Var}(y^{l})=n\operatorname{Var}(w_{i}^{l} x_{i}^{l-1}) Var(yl)=nVar(wilxil−1)继续向下展开计算,得到:
Var ( y l ) = n [ Var ( w i l ) Var ( x i l − 1 ) + Var ( w i l ) E ( x i l − 1 ) 2 + Var ( x i l − 1 ) E ( w i l ) 2 ] \operatorname{Var}\left(y^{l}\right)=n\left[\operatorname{Var}\left(w_{i}^{l}\right) \operatorname{Var}\left(x_{i}^{l-1}\right)+\operatorname{Var}\left(w_{i}^{l}\right) E\left(x_{i}^{l-1}\right)^{2}+\operatorname{Var}\left(x_{i}^{l-1}\right) E\left(w_{i}^{l}\right)^{2}\right] Var(yl)=n[Var(wil)Var(xil−1)+Var(wil)E(xil−1)2+Var(xil−1)E(wil)2]
这个式子看起来很长对吧,但是别忘了我们上面的假设一,由假设一我们可以将上式化简,得到:
Var ( y l ) = n Var ( w i l ) Var ( x i l − 1 ) \operatorname{Var}(y^{l})=n\operatorname{Var}(w_{i}^{l}) \operatorname{Var}(x_{i}^{l-1}) Var(yl)=nVar(wil)Var(xil−1)
我们清楚, y l y^{l} yl是由上一层的输入 x i l − 1 x_{i}^{l-1} xil−1计算得到的,其中需要经过激活函数的映射,但是在假设二这种情况下,此时的激活函数 f f f近似于恒等映射 ,也就是说可以认为: x i l − 1 = y l − 1 x_{i}^{l-1}=y^{l-1} xil−1=yl−1,所以,此时有:
Var ( y l ) = n Var ( w i l ) Var ( y l − 1 ) \operatorname{Var}(y^{l})=n\operatorname{Var}(w_{i}^{l}) \operatorname{Var}(y^{l-1}) Var(yl)=nVar(wil)Var(yl−1)
再回到我们一开始讨论的问题,因为我们希望每一层训练结果的方差都是稳定的,所以两层 y y y值的方差应该是相等的: Var ( y l ) = Var ( y l − 1 ) \operatorname{Var}(y^{l})=\operatorname{Var}(y^{l-1}) Var(yl)=Var(yl−1),只有这样输出结果 y y y就不会有太大波动,从而避免了梯度爆炸或者梯度消失,在这种条件下有:
n Var ( w i l ) = 1 n\operatorname{Var}(w_{i}^{l})=1 nVar(wil)=1
从而得到:
Var ( w i l ) = 1 n \operatorname{Var}(w_{i}^{l})=\frac{1}{n} Var(wil)=n1
其中 n n n代表输入层神经元的数量,也可以用 n i n n_{in} nin来表示,所以有:
Var ( w i l ) = 1 n i n \operatorname{Var}(w_{i}^{l})=\frac{1}{n_{in}} Var(wil)=nin1
此时,我们已经从正向传播的角度分析得到了参数 w i w_{i} wi的方差。那如果我们还是在以上的条件下,讨论反向传播时参数 w i w_{i} wi应该取得的方差呢?下图为上面讨论的正向传播的反向传播过程,其余假设不变:
在反向传播的过程中,我们肯定要计算损失函数 L L L对于各参数的梯度值,通过进行梯度值的计算,得到参数 w i w_{i} wi应该满足的方差,此时我们可以得到损失函数 L L L对于 l − 1 l-1 l−1层 x i x_{i} xi的梯度值 ∂ L ∂ x i l − 1 \frac{\partial L}{\partial x_{i}^{l-1}} ∂xil−1∂L为:
∂ L ∂ x i l − 1 = ∑ j = 1 m ∂ L ∂ x j l ∂ x j l ∂ y l ∂ y l ∂ x i l − 1 \frac{\partial L}{\partial x_{i}^{l-1}}=\sum_{j=1}^{m} \frac{\partial L}{\partial x_{j}^{l}} \frac{\partial x_{j}^{l}}{\partial y^{l}} \frac{\partial y^{l}}{\partial x_{i}^{l-1}} ∂xil−1∂L=j=1∑m∂xjl∂L∂yl∂xjl∂xil−1∂yl
其中,需要注意以下两点:
- ∂ x j l ∂ y l \frac{\partial x_{j}^{l}}{\partial y^{l}} ∂yl∂xjl就是激活函数 f f f的导数,由假设二可知, ∂ x j l ∂ y l = 1 \frac{\partial x_{j}^{l}}{\partial y^{l}}=1 ∂yl∂xjl=1
- 我们可以很轻松的计算得到: ∂ y l ∂ x i l − 1 = w i l \frac{\partial y^{l}}{\partial x_{i}^{l-1}}=w_{i}^l ∂xil−1∂yl=wil,因为这就是一个简单的线性运算
根据以上两点,我们可以得到:
∂ L ∂ x i l − 1 = ∑ j = 1 m ∂ L ∂ x j l w i l \frac{\partial L}{\partial x_{i}^{l-1}}=\sum_{j=1}^{m} \frac{\partial L}{\partial x_{j}^{l}} w_{i}^l ∂xil−1∂L=j=1∑m∂xjl∂Lwil
这里计算方法就与正常传播的计算过程一样,我们可以得到 ∂ L ∂ x i l − 1 \frac{\partial L}{\partial x_{i}^{l-1}} ∂xil−1∂L的方差 Var ( ∂ L ∂ x i l − 1 ) \operatorname{Var}(\frac{\partial L}{\partial x_{i}^{l-1}}) Var(∂xil−1∂L)为:
Var ( ∂ L ∂ x i l − 1 ) = m Var ( ∂ L ∂ x j l ) Var ( w i l ) \operatorname{Var}(\frac{\partial L}{\partial x_{i}^{l-1}})=m\operatorname{Var}(\frac{\partial L}{\partial x_{j}^{l}})\operatorname{Var}(w_{i}^l) Var(∂xil−1∂L)=mVar(∂xjl∂L)Var(wil)
此运算过程已介绍过,在此不再赘述。另外,我们要保证反向传播过程中计算结果的方差的稳定性,所以有:
Var ( ∂ L ∂ x i l − 1 ) = Var ( ∂ L ∂ x i l ) \operatorname{Var}(\frac{\partial L}{\partial x_{i}^{l-1}})=\operatorname{Var}(\frac{\partial L}{\partial x_{i}^{l}}) Var(∂xil−1∂L)=Var(∂xil∂L)
利用以上信息可以得到:
m Var ( w i l ) = 1 m\operatorname{Var}(w_{i}^l)=1 mVar(wil)=1
所以,最终可以得到:
Var ( w i l ) = 1 m \operatorname{Var}(w_{i}^l)=\frac{1}{m} Var(wil)=m1
其中m代表输出层神经元的个数,也可以用 n o u t n_{out} nout来表示,所以有:
Var ( w i l ) = 1 n o u t \operatorname{Var}(w_{i}^{l})=\frac{1}{n_{out}} Var(wil)=nout1
此时,我们将正向传播和反向传播的参数 w i w_{i} wi的方差做一个平均值,就可以得到Xavier初始化方法的目标方差:
Var ( w i l ) = 2 n i n + n o u t \operatorname{Var}(w_{i}^{l})=\frac{2}{n_{in}+n_{out}} Var(wil)=nin+nout2
这也就意味着,当我们的的参数 w i w_{i} wi的方差为 2 n i n + n o u t \frac{2}{n_{in}+n_{out}} nin+nout2时,可以使神经网络的训练结果更稳定,从而避免梯度消失和梯度爆炸的问题。在本节的最开始,只是对Xavier初始化方法进行了简单介绍,对于其中参数 w i w_{i} wi方差的选取只是进行了简单假设,而在这部分对此知识点进行了详细的推导,可以看到,确实可以得到我们想要的结果,那么此时我们就可以利用上面介绍过的两种初始化方法进行参数的初始化选取:
-
正态分布初始化
N ( 0 , 2 n in + n out ) \mathcal{N}\left(0, \frac{2}{n_{\text {in }}+n_{\text {out }}}\right) N(0,nin +nout 2) -
均匀分布初始化
U ( − 6 n in + n out , 6 n in + n out ) \mathcal{U}\left(-\sqrt{\frac{6}{n_{\text {in }}+n_{\text {out }}}}, \sqrt{\frac{6}{n_{\text {in }}+n_{\text {out }}}}\right) U(−nin +nout 6,nin +nout 6)
另外,还有一点需要注意,在我们的假设二中,需要满足激活函数 f f f对称,且${f}'(0)=1 $,而满足这种要求的非线性激活函数,一般只有双曲正切函数,这也证明了,Xavier初始化方法为什么适用于双曲正切函数,而不适用于ReLU激活函数。
以上就是关于Xavier初始化方法的公式推导过程,可以看到并不是很难,都是一些基础的数学知识,通过整个推导过程再结合上面介绍的基础知识,我相信各位读者一定对Xavier初始化方法有了更深刻的理解。
三、Kaiming参数初始化方法
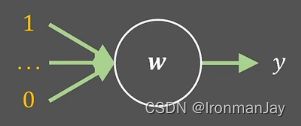
让我们考虑另外一种情况,当上一层传过来的值是使用ReLU激活函数得到的,那么大约有一半的输入会变成零,这种情况如下图所示:
那么 y y y的方差就变成了原来的一半,因为只有一半的参数“有效”,因为我们还要保证输出 y y y的值稳定,也就意味着 y y y的方差为仍为1:
Var ( y ) = 1 2 n Var ( w i ) = 1 \operatorname{Var}(y)=\frac{1}{2}n \operatorname{Var}\left(w_{i}\right)=1 Var(y)=21nVar(wi)=1
所以,参数 w i w_{i} wi的方差变为:
Var ( w i ) = 2 n \operatorname{Var}(w_{i})=\frac{2}{n} Var(wi)=n2
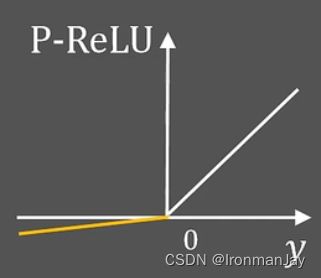
刚才讨论的情况是使用ReLU函数作为激活函数的情况,那如果上一层使用P-ReLU函数作为激活函数,其函数图像如下所示:
P-ReLU激活函数的解析式如下所示:
P-ReLU ( y ) = { y , y > 0 α y , y ≤ 0 \operatorname{P-ReLU}(y)=\left\{\begin{array}{ll} y, & y>0 \\ \alpha y, & y \leq 0 \end{array}\right. P-ReLU(y)={y,αy,y>0y≤0
如果我们使用P-ReLU函数作为激活函数,那么参数 w i w_{i} wi的方差就变为:
Var ( w i ) = 2 n ( 1 + α 2 ) \operatorname{Var}(w_{i})=\frac{2}{n(1+\alpha^{2})} Var(wi)=n(1+α2)2
可以看到与使用ReLU函数作为激活函数时的差别为分母的 1 + α 2 1+\alpha^{2} 1+α2,因为我们要考虑到修正对参数初始化的影响。现在我们已经得到了在分别使用ReLU激活函数和P-ReLU激活函数情况下参数 w i w_{i} wi的方差,也就是说,当参数 w i w_{i} wi的方差为我们上面讨论的结果时,输出 y y y的值是稳定的,当输出 y y y的值稳定后,就会避免梯度消失和梯度爆炸的问题,也就会让模型的训练精度更高。
3.1 正态分布参数初始化
有了上面讨论的基础后,并且已经得到了参数 w i w_{i} wi的方差,那么很自然的就能求出当参数 w i w_{i} wi应该服从的正态分布:
N ( 0 , 2 n ( 1 + α 2 ) ) \mathcal{N}\left(0, \frac{2}{n(1+\alpha^{2})}\right) N(0,n(1+α2)2)
3.2 均匀分布参数初始化
同理,我们也可以写出参数 w i w_{i} wi应该服从的均匀分布:
U ( − 6 n ( 1 + α 2 ) , 6 n ( 1 + α 2 ) ) \mathcal{U}\left(-\sqrt{\frac{6}{n(1+\alpha^{2})}}, \sqrt{\frac{6}{n(1+\alpha^{2})}}\right) U(−n(1+α2)6,n(1+α2)6)
以上讨论的内容就是2015年提出来的Kaiming初始化方法,此种方法适用于当激活函数为ReLU函数时的情况。
3.3 Kaiming参数初始化方法目标方差推导
当我们进行Kaiming初始化方法目标方差的推导时,仍考虑同样的神经元的正向传播过程,而且此时的激活函数 f f f为ReLU激活函数,整个过程如下图所示:
此时的假设条件有些变化:
- 假设一: E ( w ) = 0 E(w)=0 E(w)=0
- 假设二: x x x的方差都是相等的
并且我们仍需要使用到三个基础公式:
-
公式一:
Var ( X ) = E ( X 2 ) − E ( X ) 2 \operatorname{Var}(X)=E\left(X^{2}\right)-E(X)^{2} Var(X)=E(X2)−E(X)2 -
公式二:
Var ( X + Y ) = Var ( X ) + Var ( Y ) \operatorname{Var}(X+Y)=\operatorname{Var}(X)+\operatorname{Var}(Y) Var(X+Y)=Var(X)+Var(Y)
- 公式三:
Var ( X Y ) = Var ( X ) Var ( Y ) + Var ( X ) E ( Y ) 2 + Var ( Y ) E ( X ) 2 \operatorname{Var}(XY)=\operatorname{Var}(X)\operatorname{Var}(Y)+\operatorname{Var}(X)E(Y)^2+\operatorname{Var}(Y)E(X)^2 Var(XY)=Var(X)Var(Y)+Var(X)E(Y)2+Var(Y)E(X)2
前面的推导过程都与Xavier初始化方法的推导过程一样,我们仍旧可以得到:
Var ( y l ) = n Var ( w i l x i l − 1 ) \operatorname{Var}(y^{l})=n\operatorname{Var}(w_{i}^{l}x_{i}^{l-1}) Var(yl)=nVar(wilxil−1)
仍然使用公式三对其进行展开计算:
Var ( y l ) = n [ Var ( w i l ) Var ( x i l − 1 ) + Var ( w i l ) E ( x i l − 1 ) 2 + Var ( x i l − 1 ) E ( w i l ) 2 ] \operatorname{Var}\left(y^{l}\right)=n\left[\operatorname{Var}\left(w_{i}^{l}\right) \operatorname{Var}\left(x_{i}^{l-1}\right)+\operatorname{Var}\left(w_{i}^{l}\right) E\left(x_{i}^{l-1}\right)^{2}+\operatorname{Var}\left(x_{i}^{l-1}\right) E\left(w_{i}^{l}\right)^{2}\right] Var(yl)=n[Var(wil)Var(xil−1)+Var(wil)E(xil−1)2+Var(xil−1)E(wil)2]
由假设一,我们可以继续得到:
Var ( y l ) = n [ Var ( w i l ) Var ( x i l − 1 ) + Var ( w i l ) E ( x i l − 1 ) 2 ] \operatorname{Var}\left(y^{l}\right)=n\left[\operatorname{Var}\left(w_{i}^{l}\right) \operatorname{Var}\left(x_{i}^{l-1}\right)+\operatorname{Var}\left(w_{i}^{l}\right) E\left(x_{i}^{l-1}\right)^{2}\right] Var(yl)=n[Var(wil)Var(xil−1)+Var(wil)E(xil−1)2]
由公式一,我们可以继续得到:
Var ( y l ) = n [ Var ( w i l ) E [ ( x i l − 1 ) 2 ] − Var ( w i l ) E ( x i l − 1 ) 2 + Var ( w i l ) E ( x i l − 1 ) 2 ] \operatorname{Var}(y^{l})=n[\operatorname{Var}(w_{i}^{l}) E[(x_{i}^{l-1})^2]-\operatorname{Var}(w_{i}^{l}) E(x_{i}^{l-1})^{2} + \operatorname{Var}(w_{i}^{l}) E(x_{i}^{l-1})^{2}] Var(yl)=n[Var(wil)E[(xil−1)2]−Var(wil)E(xil−1)2+Var(wil)E(xil−1)2]
可以注意到,上式最后两项互为相反数,所以可以得到:
Var ( y l ) = n Var ( w i l ) E [ ( x i l − 1 ) 2 ] \operatorname{Var}(y^{l})=n\operatorname{Var}(w_{i}^{l}) E[(x_{i}^{l-1})^2] Var(yl)=nVar(wil)E[(xil−1)2]
因为第 l − 1 l-1 l−1层的 x i x_{i} xi是第 l − 1 l-1 l−1层的 y y y经过ReLU激活函数 f f f得到的,所以有: x i l − 1 = f ( y l − 1 ) x_{i}^{l-1}=f(y^{l-1}) xil−1=f(yl−1),那么上式又等于:
Var ( y l ) = n Var ( w i l ) E [ ( f ( y l − 1 ) ) 2 ] \operatorname{Var}(y^{l})=n\operatorname{Var}(w_{i}^{l}) E[(f(y^{l-1}))^2] Var(yl)=nVar(wil)E[(f(yl−1))2]
根据概率论与数理统计中关于概率密度的知识可以得到:
E [ ( f ( y l − 1 ) ) 2 ] = ∫ − ∞ + ∞ f ( y l − 1 ) 2 p ( y l − 1 ) d ( y l − 1 ) E\left[\left(f\left(y^{l-1}\right)\right)^{2}\right]=\int_{-\infty}^{+\infty} f\left(y^{l-1}\right)^{2} p\left(y^{l-1}\right) d\left(y^{l-1}\right) E[(f(yl−1))2]=∫−∞+∞f(yl−1)2p(yl−1)d(yl−1)
因为激活函数 f f f为ReLU激活函数,所以不需要积分小于零的部分(因为小于零时,函数值为零),而且大于零的部分 f ( y ) = y f(y)=y f(y)=y,所以通过上式可以得到:
E [ ( f ( y l − 1 ) ) 2 ] = ∫ 0 + ∞ ( y l − 1 ) 2 p ( y l − 1 ) d ( y l − 1 ) + ∫ − ∞ 0 α 2 ( y l − 1 ) 2 p ( y l − 1 ) d ( y l − 1 ) E\left[\left(f\left(y^{l-1}\right)\right)^{2}\right]=\int_{0}^{+\infty}\left(y^{l-1}\right)^{2} p\left(y^{l-1}\right) d\left(y^{l-1}\right)+\int_{-\infty}^{0} \alpha^{2}\left(y^{l-1}\right)^{2} p\left(y^{l-1}\right) d\left(y^{l-1}\right) E[(f(yl−1))2]=∫0+∞(yl−1)2p(yl−1)d(yl−1)+∫−∞0α2(yl−1)2p(yl−1)d(yl−1)
上式的第一部分就是从零到正无穷的积分,并且可以拿掉激活函数 f f f的表达式,需要注意的是第二部分,因为Parametric ReLU激活函数和Leaky ReLU激活函数中负半轴的函数值并不为零,而是和 α \alpha α有关系,并不一直为零,所以也要考虑上,如果使用ReLU激活函数就不用写第二部分,其中 α \alpha α是负半轴激活函数的斜率值。此时,经过积分的计算与期望的概率密度知识我们可以得到:
E [ ( f ( y l − 1 ) ) 2 ] = 1 2 E [ ( y l − 1 ) 2 ] + 1 2 α 2 E [ ( y l − 1 ) 2 ] E\left[\left(f\left(y^{l-1}\right)\right)^{2}\right]=\frac{1}{2}E[(y^{l-1})^2] + \frac{1}{2}\alpha^{2}E[(y^{l-1})^2] E[(f(yl−1))2]=21E[(yl−1)2]+21α2E[(yl−1)2]
将上式得到的 E [ ( f ( y l − 1 ) ) 2 ] E\left[\left(f\left(y^{l-1}\right)\right)^{2}\right] E[(f(yl−1))2]带入到 Var ( y l ) = n Var ( w i l ) E [ ( f ( y l − 1 ) ) 2 ] \operatorname{Var}(y^{l})=n\operatorname{Var}(w_{i}^{l}) E[(f(y^{l-1}))^2] Var(yl)=nVar(wil)E[(f(yl−1))2]中可以得到:
Var ( y l ) = 1 2 n ( 1 + α 2 ) Var ( w i l ) E [ ( y l − 1 ) 2 ] \operatorname{Var}(y^{l})=\frac{1}{2}n(1+\alpha^{2})\operatorname{Var}(w_{i}^{l}) E[(y^{l-1})^{2}] Var(yl)=21n(1+α2)Var(wil)E[(yl−1)2]
另外,由公式一可以得到:
E [ ( y l − 1 ) 2 ] = Var ( y l − 1 ) + E [ ( y l − 1 ) ] 2 E[(y^{l-1})^2]=\operatorname{Var}(y^{l-1})+E[(y^{l-1})]^{2} E[(yl−1)2]=Var(yl−1)+E[(yl−1)]2
由假设一可知, E [ ( y l − 1 ) ] 2 = 0 E[(y^{l-1})]^{2}=0 E[(yl−1)]2=0,所以可以得到:
E [ ( y l − 1 ) 2 ] = Var ( y l − 1 ) E[(y^{l-1})^2]=\operatorname{Var}(y^{l-1}) E[(yl−1)2]=Var(yl−1)
有了这个等式,将其带入到 Var ( y l ) = 1 2 n ( 1 + α 2 ) Var ( w i l ) E [ ( y l − 1 ) 2 ] \operatorname{Var}(y^{l})=\frac{1}{2}n(1+\alpha^{2})\operatorname{Var}(w_{i}^{l}) E[(y^{l-1})^{2}] Var(yl)=21n(1+α2)Var(wil)E[(yl−1)2]中可以得到:
Var ( y l ) = 1 2 n ( 1 + α 2 ) Var ( w i l ) Var ( y l − 1 ) \operatorname{Var}(y^{l})=\frac{1}{2}n(1+\alpha^{2})\operatorname{Var}(w_{i}^{l}) \operatorname{Var}(y^{l-1}) Var(yl)=21n(1+α2)Var(wil)Var(yl−1)
为了使神经网络的输出值稳定,所以我们仍希望每一层 y y y的方差是稳定的,所以令:
Var ( y l ) = Var ( y l − 1 ) \operatorname{Var}(y^{l})=\operatorname{Var}(y^{l-1}) Var(yl)=Var(yl−1)
那么,经过计算可以得到:
1 2 n ( 1 + α 2 ) Var ( w i l ) = 1 \frac{1}{2}n(1+\alpha^{2})\operatorname{Var}(w_{i}^{l})=1 21n(1+α2)Var(wil)=1
从而有:
Var ( w i l ) = 2 n ( 1 + α 2 ) \operatorname{Var}(w_{i}^{l})=\frac{2}{n(1+\alpha^{2})} Var(wil)=n(1+α2)2
这时我们就得到了Kaiming初始化方法的目标方差,而反向传播过程同理,在此不再赘述,当我们得到Kaiming初始化方法的目标方差后,就可以使用上面介绍的两种初始化方法进行参数的初始化选取:
-
正态分布初始化
N ( 0 , 2 n ( 1 + α 2 ) ) \mathcal{N}\left(0, \frac{2}{n(1+\alpha^{2})}\right) N(0,n(1+α2)2) -
均匀分布初始化:
U ( − 6 n ( 1 + α 2 ) , 6 n ( 1 + α 2 ) ) \mathcal{U}\left(-\sqrt{\frac{6}{n(1+\alpha^{2})}}, \sqrt{\frac{6}{n(1+\alpha^{2})}}\right) U(−n(1+α2)6,n(1+α2)6)
以上介绍的就是关于Kaiming初始化方法的目标方差推导过程,可以看到整个过程还是稍稍复杂一些,但是经过计算后也得到了我们想要的结果,这样就可以让我们的神经网络训练效果更好,从而避免梯度消失或者梯度爆炸问题。另外,通过以上的推导过程,也可以看到,Kaiming初始化方法适用于ReLU系列的激活函数。
总结
以上就是本文的全部内容,内容确实不少,我也总结了好久,希望读者可以学到自己需要的知识,加油!