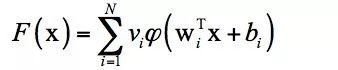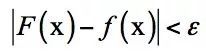卷积神经网络 [数学特性]

神经网络代表了人工智能中的连接主义思想，它是一种仿生的方法，被看做是对动物大脑神经系统的模拟。在实现时，它又和大脑的结构不同。从数学上看，多层神经网络本质上是一个复合函数。

既然神经网络在本质上是一个复杂的复合函数，这会让我们思考一个问题：这个函数的建模能力有多强？即它能模拟什么样的目标函数？已经证明，只要激活函数选择得当，神经元个数足够多，使用3层即包含一个隐含层的神经网络就可以实现对任何一个从输入向量到输出向量的连续映射函数的逼近[1][2][3]，这个结论称为万能逼近（universal approximation）定理。

文献[3]对使用sigmoid激活函数时的情况进行了证明。文献[1]指出，万能逼近特性并不取决于神经网络具体的激活函数，而是由神经网络的结构保证的。

万能逼近定理的表述为：如果是一个非常数、有界、单调递增的连续函数，是m维的单位立方体，中的连续函数空间为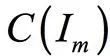。对于任意以及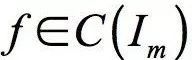函数，存在整数N，实数，实向量，通过它们构造函数作为函数f的逼近：

对任意的满足

万能逼近定理的直观解释是可以构造出上面这样的函数，逼近定义在单位立方体空间中的任何一个连续函数到任意指定的精度。这一结论和多项式逼近类似，后者利用多项式函数来逼近任何连续函数到任何精度。这个定理的意义在于，从理论上保证了神经网络的拟合能力。

但是这只是一个理论结果，具体实现时，神经网络需要多少层，每层要多少个神经元？这些问题只能通过实验和经验来确定，以保证效果。另外一个问题是训练样本，要拟合出一个复杂的函数需要大量的训练样本，而且面临过拟合的问题。这些工程实现的细节也至关重要，卷积网络在1989年就已经出现了，为什么直到2012年才取得成功？答案有这么几点：

1. 训练样本数量的限制。早期的训练样本非常少，没有大规模采集，不足以训练出一个复杂的卷积网络。
2. 计算能力的限制。1990年代的计算机能力太弱，没有GPU这样的高性能计算技术，要训练一个复杂的神经网络不现实。
3. 算法本身的问题。神经网络长期以来存在梯度消失的问题，由于反向传播时每一层都要乘上激活函数的导数值，如果这个导数的绝对值小于1，次数多了之后梯度很快趋近于0，使得前面的层无法得到更新。

AlexNet网络的规模尤其是层数比之前的网络更深，使用了ReLU作为激活函数，抛弃了sigmoid和tanh函数，一定程度上缓解了梯度消失问题。加上Dropout机制，还减轻了过拟合问题。这些技术上的改进，加上ImageNet这样的大样本集，以及GPU的计算能力，保证了它的成功。后面的研究表明，加大网络的层数、参数数量，能够明显的增加网络的精度。对于这些问题，SIGAI会在后面的专题文章中详细介绍，感兴趣的读者可以关注我们的公众号。

卷积神经网络本质上权重共享的全连接神经网络，因此万能逼近定理对它是适用的。但卷积网络的卷积层，池化层又具有其特性。文献[11]从数学的角度对深层卷积网络进行了解释。在这里，作者将卷积网络看做是用一组级联的线性加权滤波器和非线性函数对数据进行散射。通过对这一组函数的压缩（contraction）和分离（separation）特性进行分析从而解释深度卷积网络的建模能力。另外，还解释了深度神经网络的迁移特性。卷积神经网络的卷积操作分为两步，第一步是线性变换，第二步是激活函数变换。前者可以看成是将数据线性投影到更低维的空间；后者是对数据的压缩非线性变换。作者对这几种变换的分离和压缩特性分别进行了分析。

参考文献：

[1] Kurt Hornik. Approximation capabilities of multilayer feedforward networks. 1991, Neural Networks.

[2] Hornik, K., Stinchcombe, M., and White, H. Multilayer feedforward networks are universal approximators. Neural Networks, 2, 359-366, 1989.

[3] Cybenko, G. Approximation by superpositions of a sigmoid function. Mathematics of Control, Signals, and Systems, 2, 303-314, 1989.