【集成学习系列教程2】AdaBoost回归算法原理及sklearn应用

4 AdaBoost回归算法

4.1 概要

AdaBoost算法不仅可以用于分类任务，还可以用于回归任务。由于回归预测得到的结果是连续数值，如股票价格，由于股票价格走势曲线是连续的，所以股票价格在实数范围内有非常多可能的数值，不像分类任务中的类别标签一样仅仅只有若干个固定的整数值。由于在分类任务中，样本权重的更新幅度与样本的类别息息相关，而在回归任务中用“目标数值”代替了分类标签，因此，AdaBoost回归算法更新样本权重的方式与AdaBoost分类算法有较大差异。下面将对AdaBoost回归算法做详细介绍。

4.2 算法步骤

假设有一个如下数据集，它由$m$个样本组成：
$$D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),...,({\mathbf{x}}_m,y_m)\}$$
其中，${\mathbf{x}}_i\in {\mathbb{R}}^d$（每一个样本数据有 $d$ 个特征），$y_i$为样本${\mathbf{x}}_i$的目标数值 。AdaBoost回归算法的具体步骤如下：

1. 初始化权重。记初始状态下的数据集样本分布为 $Dis{t}_1$，对每一个样本${\mathbf{x}}_i$的权重均初始化为$1/m$，则$Dis{t}_1({\mathbf{x}}_i)=1/m$。$Dis{t}_1$分布用于第一个弱分类器$h_1$的训练，$Dis{t}_t$分布用于第一个弱分类器$h_t$的训练，其他同理；

2. 循环进行 $T$ 轮迭代，记每一轮迭代中弱分类器的编号为 $t$，且$t\in \{1,2,3,...,T\}$。以该步骤作为循环体，循环体中的步骤进一步细分为：

   1. 在样本分布为 $Dis{t}_t(\mathbf{x})$的基础上，在数据集$D$上训练弱分类器$h_t$；

   2. 计算分类器$h_t$在训练集$D$上的最大误差$E_t$，计算公式为：
      $$E_t=max|y_i-h_t({\mathbf{x}}_i)|,i=1,2,...,m$$
      其中，$h_t({\mathbf{x}}_i)$表示弱分类器$h_t$对样本${\mathbf{x}}_i$的预测结果，$y_i$表示样本${\mathbf{x}}_i$的目标数值；

   3. 根据上面求得的$h_t$的最大误差$E_t$，计算$h_t$对每个样本的相对误差，其计算方法有很多种，这里以平方误差为例：
      $$e_{ti}=\frac{(y_i-h_t({\mathbf{x}}_i){)}^2}{E_t^2},i=1,2,...,m$$

   4. 根据上一步求得的样本相对误差$e_{ti}$，计算出当前弱分类器$h_t$的误差率：
      $$e_t=\sum _{i=1}^{m}Dis{t}_t({\mathbf{x}}_i)e_{ti}$$
      即数据集中所有样本的权重与误差之乘积的和；

   5. 更新当前弱分类器$h_t$的权重，计算公式为：
      $$w_t=\frac{e_t}{1-e_t}$$

      6. 更新数据集样本的权重分布，对于样本${\mathbf{x}}_i$，更新权重的计算公式为：
         $$Dis{t}_{t+1}({\mathbf{x}}_i)=\frac{Dis{t}_t({\mathbf{x}}_i)}{Z_t}{w}_t^{1-e_{ti}}$$
         其中，$Z_t$为归一化因子，其计算公式为：
         $$Z_t=\sum _{i=1}^{m}Dis{t}_t({\mathbf{x}}_i)w_t^{1-e_{ti}}$$

   6. 令$t:=t+1$，回到循环体中的步骤1。

3. 结束$T$轮迭代，最终得到强回归器如下：
   $$H(\mathbf{x})=\sum _{i=1}^{m}ln(\frac{1}{w_t})f(\mathbf{x})=[\sum _{i=1}^{m}ln(\frac{1}{w_t})]f(\mathbf{x})$$
   其中，$f(\mathbf{x})$是所有$w_t{h}_t(\mathbf{x})$ $(t=1,2,...,T)$的中位数，即所有弱学习器的加权输出结果的中位数。

   这样就完成了AdaBoost算法的全过程。

4.3 sklearn中的AdaBoost回归

sklearn中的AdaBoostRegressor类对AdaBoost回归算法进行了实现，供用户使用。下面将对这个类进行详细介绍。

4.3.1 原型

原型如下：
class sklearn.ensemble.AdaBoostRegressor(base_estimator=None, *, n_estimators=50, learning_rate=1.0, loss='linear', random_state=None)[source]

4.3.2 参数

上述原型中各参数的解释如下，其中一些参数的含义与AdaBoostClassifier类的一致，因此对这些参数就不做详细介绍，读者可以翻到1.4小节查阅。

• base_estimator： 对象类型，默认值为None
  该参数不指定时，使用DecisionTreeRegressor(max_depth=3)作为基学习器，即默认使用深度为3的回归决策树。

• n_estimators： 整型，默认值为50
  基学习器的最大迭代次数（即最大的基学习器个数）。

• learning_rate： 浮点型，默认为1.0
  表示每个基学习器的权重缩减系数。

• loss：可选项为 {‘linear’, ‘square’, ‘exponential’}，默认为‘linear’

  定义误差函数（即1.7.2小节中的$e_{ti}$），各个选项的含义如下：

  • ‘linear’：线性损失函数
  • ‘square’：平方损失函数
  • ‘exponential’：指数损失函数

• random_state： 整型，默认为None
  为每个基学习器设置相同的随机数种子，确保多次运行所生成的随机数状态均一致，便于调参与观察。

4.3.3 属性

AdaBoostingRegressor类的全部属性只有5个，比AdaBoostingClassifier类少。如下：

• base_estimator_：返回基学习器（包括种类、详细参数等信息）。
• estimators_：返回对数据集进行拟合之后的所有基学习器所组成的列表。
• estimator_weights_：返回每个基学习器所对应权重所组成的列表。
• estimator_errors_：返回每个基学习器的回归损失所组成的列表。
• feature_importances_：返回数据集中每个特征的权重的组成的列表。

4.3.4 常用方法

AdaBoostingRegressor类的常用方法如下：

• fit(X,y,[,sample_weight]：拟合数据集。
• get_params([deep])：$deep$参数指定为 $True$ 时，返回集成回归器的各项参数值。
• predict(X)：对样本数据集$X$进行回归预测，返回预测出的数值。
• staged_predict(X)：获取对数据集$X$的阶梯测试准确率（1.6.3小节对这个概念已有介绍）。
• staged_score(X)：获取对数据集$X$的阶梯训练准确率（1.6.3小节对这个概念已有介绍）。
• set_params(**params)：以字典的形式传入参数**params，设置集成学习器的各项参数。

4.4 实例3：使用AdaBoostRegressor完成回归任务

接下来将演示如何使用AdaBoostRegressor类完成一个简单的回归任务，并对不同参数取值下的拟合效果进行可视化，使得读者可以直观感受到各个参数的作用。

4.4.1 数据集的创建与可视化

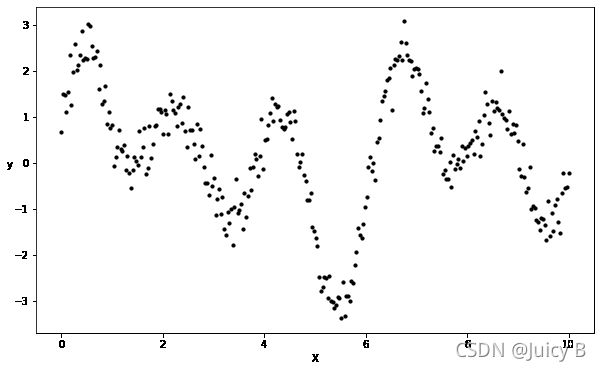
这里选择叠加正弦曲线，并加上高斯噪声的方式来创建数据集。这样的数据集非常适合用来测试、对比和可视化回归算法的性能。代码如下：

# 创建随机数种子
rng = np.random.RandomState(111)
# 训练集X为300个0到10之间的随机数
X = np.linspace(0, 10, 300)[:, np.newaxis]
# 定义训练集X的目标变量
y = np.sin(1*X).ravel() + np.sin(2*X).ravel() + np.sin(3* X).ravel()+np.cos(3*X).ravel() +rng.normal(0, 0.3, X.shape[0])

plt.figure(figsize=(10, 6))
plt.scatter(X, y, c='k', label='data', s=10, zorder=1, edgecolors=(0, 0, 0))
plt.xlabel("X")
plt.ylabel("y", rotation=0)
plt.show()

输出结果如下：

图1.4.1: 通过叠加正弦曲线并添加高斯噪声的方式所创建的数据集

4.4.2 不同参数的AdaBoost回归器拟合效果对比

接下来将从两个方面对比不同参数取值下AdaBoost回归器的回归效果。

1 固定基学习器最大深度

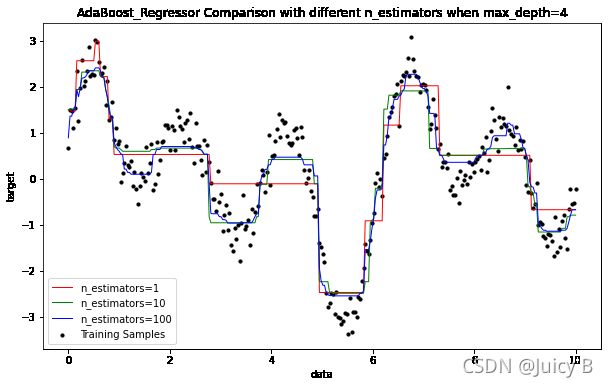
固定基学习器（回归决策树）的最大深度为4，调节迭代次数分别为1、10和100，对比拟合效果。

代码如下：

# 定义不同迭代次数的AdaBoost回归器模型
adbr_1 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=1, random_state=123)
adbr_2 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=10, random_state=123)
adbr_3 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=100, random_state=123)

# 拟合上述三个模型
adbr_1.fit(X, y)
adbr_2.fit(X, y)
adbr_3.fit(X, y)

# 读取各个模型的最大迭代次数
adbr_1_n_estimators = adbr_1.get_params(True['n_estimators']
adbr_2_n_estimators = adbr_2.get_params(True['n_estimators']
adbr_3_n_estimators = adbr_3.get_params(True)['n_estimators']

# 预测
y_1 = adbr_1.predict(X)
y_2 = adbr_2.predict(X)
y_3 = adbr_3.predict(X)
# 画出各个模型的回归拟合效果
plt.figure(figsize=(10, 6))
# 画出训练数据集（用黑色表示）
plt.scatter(X, y, c="k", s=10, label="Training Samples")
# 画出adbr_1模型（最大迭代次数为1)的拟合效果（用红色表示）
plt.plot(X, y_1, c="r", label="n_estimators=%d" % adbr_1_n_estimators, linewidth=1)
# 画出adbr_2模型（最大迭代次数为10)的拟合效果（用绿色表示）
plt.plot(X, y_2, c="g", label="n_estimators=%d" % adbr_2_n_estimators, linewidth=1)
# 画出adbr_3模型（最大迭代次数为100)的拟合效果（用蓝色表示）
plt.plot(X, y_3, c="b", label="n_estimators=%d" % adbr_3_n_estimators, linewidth=1)

plt.xlabel("data")
plt.ylabel("target")
plt.title("AdaBoost_Regressor Comparison with different n_estimators when max_depth=3")
plt.legend()
plt.show()

输出结果如下：

图1.4.2: 基学习器深度为4时，不同迭代次数下AdaBoost回归算法在数据集上的拟合效果对比

可以看到，随着迭代次数的增加，AdaBoost回归器对数据的拟合效果变得越来越好，但是在迭代次数呈指数级增加的情况下，拟合效果并没有得到很明显的提升。由此可以推测，在基学习器的深度不够大的情况下，大幅增加迭代次数对缓解欠拟合的帮助并不大。接下来，我们尝试改变基学习器的最大深度，看看效果如何。

2 固定迭代次数

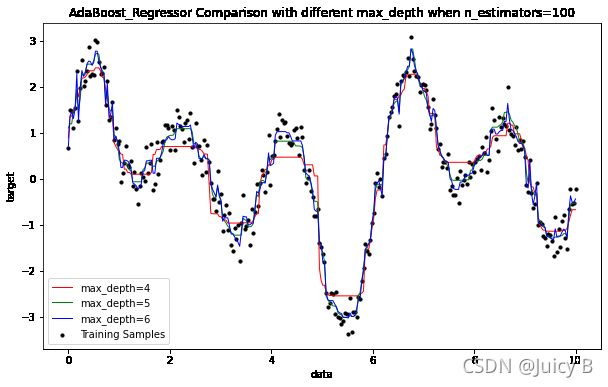
固定迭代次数为100，调节基学习器（回归决策树）的最大深度，分别为4、5、6，对比拟合效果。

代码如下：

# 拟合不同基学习器深度的回归模型
adbr_4 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=100, random_state=123)
adbr_5 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=5), n_estimators=100, random_state=123)
adbr_6 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=6), n_estimators=100, random_state=123)

# 拟合上述3个模型
adbr_4.fit(X, y)
adbr_5.fit(X, y)
adbr_6.fit(X, y)

# 预测
y_4 = adbr_4.predict(X)
y_5 = adbr_5.predict(X)
y_6 = adbr_6.predict(X)

# 画出各个模型的回归拟合效果
plt.figure(figsize=(10, 6))
# 画出训练数据集（用黑色表示）
plt.scatter(X, y, c="k", s=10, label="Training Samples")
# 画出adbr_4模型（基学习器深度为3)的拟合效果（用红色表示）
plt.plot(X, y_4, c="r", label="max_depth=4" , linewidth=1)
# 画出adbr_5模型（基学习器深度为4)的拟合效果（用绿色表示）
plt.plot(X, y_5, c="g", label="max_depth=5" , linewidth=1)
# 画出adbr_6模型（基学习器深度为5)的拟合效果（用蓝色表示）
plt.plot(X, y_6, c="b", label="max_depth=6" , linewidth=1)

plt.xlabel("data")
plt.ylabel("target")
plt.title("AdaBoost_Regressor Comparison with different max_depth when n_estimators=100")
plt.legend()
plt.show()

输出结果如下：

图1.4.3: 迭代次数为100时不同基学习器深度下AdaBoost回归算法在数据集上的拟合效果对比

可以看到，在固定迭代次数为100的情况下，增加基学习器的最大深度对提升拟合效果的帮助非常大。所以，实际使用中，在控制拟合时间的前提下，读者应该尽量将基学习器回归决策树的最大深度设置得大一点，然后再在此基础上尝试对n_estimators等参数进行调参。