【DS】栈与集合Stack的理解和使用

一.栈（Stack）的概念

1. 概念

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。我们自己去实现栈可以用数组或者双链表来完成 。

Java集合中的Stack类在底层其实就是一个数组空间 , 当然LinkedList底层是一个双链表，所以LinkedList也可以当做栈来使。

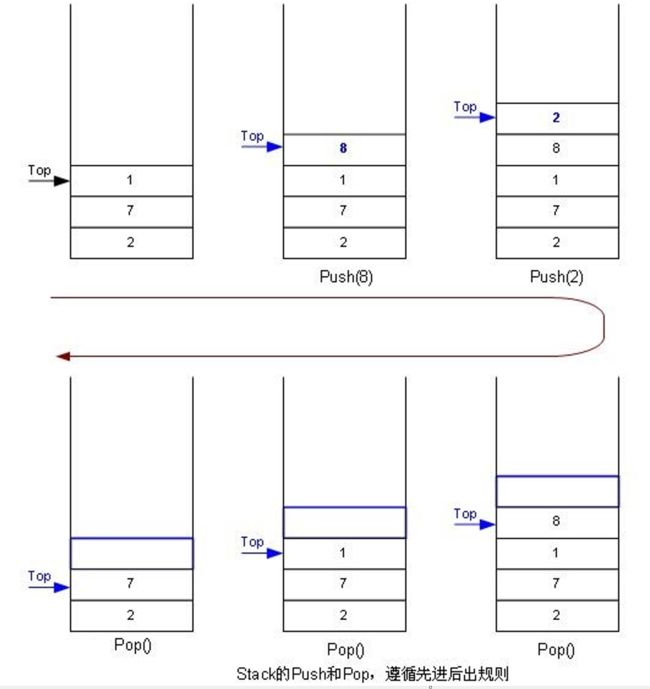
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。

出栈：栈的删除操作叫做出栈。出数据在栈顶。

2. 栈在现实生活中的例子

二.栈的使用

1. 集合-Stack类的介绍

在集合框架中 , Stack的继承实现关系如下:

从上图中可以看到，Stack继承了Vector，Vector和ArrayList类似，都是动态的顺序表，不同的Vector是线程安全；Vector类，是线程安全的动态数组，但是性能较差 , 现在已经不是很常用了 , 可以说已经过时了。

2. 常用方法

方法	功能
Stack()	构造一个空的栈
E push(E e)	将e入栈，并返回e
E pop(	将栈顶元素出栈并返回
E peek()	获取栈顶元素
int size()	获取栈中有效元素个数
boolean empty()	检测栈是否为空

3. 代码实现

public static void main(String[] args) {
        Stack s = new Stack();
        s.push(1);
        s.push(2);
        s.push(3);
        s.push(4);
        System.out.println(s.size()); // 获取栈中有效元素个数---> 4
        System.out.println(s.peek()); // 获取栈顶元素---> 4
        s.pop(); // 4出栈，栈中剩余1 2 3，栈顶元素为3
        System.out.println(s.pop()); // 3出栈，栈中剩余1 2 栈顶元素为3
        if(s.empty()){
            System.out.println("栈空");
        }else{
            System.out.println(s.size());
        }
    }

三.栈的模拟实现

由于Java集合中的Stack类在底层是一个顺序表 , 所以这里用数组来模拟实现栈 。

1. 代码实现

import java.util.Arrays;
import java.util.EmptyStackException;
import java.util.Stack;

/**
 * Created with IntelliJ IDEA.
 * Description:
 * User:YY
 * Date:2023-02-15
 * Time:15:47
 */
public class MyStack {
    int[] array;
    int size;

    public MyStack() {
        this.array = new int[4];
    }
    //入栈操作
    public int push(int e) {
        //栈满了吗？是否扩容？
        ensureCapacityHelper();
        this.array[size++] = e;
        return e;
    }
    private void ensureCapacityHelper() {
        // overflow-conscious code
        if (this.size - this.array.length >= 0){
            this.array = Arrays.copyOf(this.array,this.array.length * 2);
        }
    }
    //出栈
    public int pop(){
        if(this.size() == 0){
            throw new EmptyException("栈空异常");
        }
        int e = peek();
        this.size--;
        return e;
    }
    //栈顶元素
    public int peek() throws EmptyException{
        if(this.size() == 0){
            throw new EmptyException("栈空异常");
        }
        return this.array[this.size() - 1];
    }
    public int size(){
        return this.size;
    }

    public static void main(String[] args) {
        MyStack myStack = new MyStack();
        myStack.push(1);
        myStack.push(2);
        myStack.push(3);
        myStack.push(4);
        myStack.push(5);
        System.out.println(myStack.size());
        int length = myStack.array.length;
        System.out.println(length);
        System.out.println("------------------------");

        int x1 = myStack.pop();
        System.out.println(x1);
        x1 = myStack.pop();
        System.out.println(x1);
        System.out.println(myStack.size());
        System.out.println("------------------------");

        int x2 = myStack.peek();
        System.out.println(x2);
        x2 = myStack.peek();
        System.out.println(x2);
    }
}

2. 执行结果

3. 思考总结

如果使用链表来实现栈 , 如何操作入栈和出栈更方便一些呢?

首先考虑单链表 , 假设单链表中有head和tail两个引用指向头节点和尾节点 , 那么如果是尾插入栈 , 时间复杂度为O(1) , 但此时出栈 , 需要找到尾节点的前一个节点 , 出栈的时间复杂度就为O(N)了 ; 再看头插入栈 , 时间复杂度为O(1) , 此时出栈也是从头出 , 时间复杂度为O(1) ;

所以如果采用单链表来实现栈应该采用头插法入栈 .

再考虑双链表来实现栈 , 由于节点之间是双向的 , 所以入栈采用头插和尾插都可 , 最终入栈和出栈的时间复杂度都为O(1) , 所以采用双向链表来实现栈还是很方便的 .

四.栈的应用场景

1. 改变元素序列

1. 若进栈序列为 1,2,3,4 ， 进栈过程中可以出栈，则下列不可能的一个出栈序列是（ C）
A: 1,4,3,2 B: 2,3,4,1 C: 3,1,4,2 D: 3,4,2,1

选项A： 1入栈，1出栈，2，3，4依次入栈，4，3，2 依次出栈 , 出栈序列为1，4，3，2 ，所以选项A的出栈序列是可能的。

选项B： 1，2依次入栈，2出栈，3入栈，3出栈，4入栈，4出栈，1出栈 , 出栈序列为2，3，4，1 ，所以选项C的出栈序列是可能的。

选项C： 1，2，3依次入栈，3出栈，选项中的第二个出栈序列为1 , 但此时3出栈后栈顶元素为2 , 不可能是1出栈 , 所以选项C的出栈序列是不可能的。

选项D： 1，2，3依次入栈，3出栈，4入栈，4出栈，2，1依次出栈，出栈序列为3，4，2，1 ，所以选项D的出栈序列是可能的。

2.一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈，然后再依次出栈，则元素出栈的顺序是（B）。
A: 12345ABCDE B: EDCBA54321 C: ABCDE12345 D: 54321EDCBA

2. 中缀表达式

我们常用的数学加减乘除运算表达式都是中缀表达式，比如 1+2+3∗4，将中缀表达式按运算顺序打上不同的括号对，分别将运算符移到对应括号最右边，再将所有括号擦除，就能得到后缀表达式，同理将运算符移到到对应括号最左边就是前缀表达式。

后续我们在面试刷题过程中，常会遇到用代码求后缀表达式的值，这里可采用栈的方式来实现，具体可见后续章节，OJ如下：150. 逆波兰表达式求值 - 力扣（LeetCode）

3. 将递归转为循环

比如：逆序打印链表

// 递归方式打印单链表
    public void display2(ListNode head){
        if(this.head == null){
            return;
        }
        if(this.head.next == null){
            System.out.println(this.head.val + " ");
            return;
        }
        display2(this.head.next);
        System.out.println(this.head.val + " ");
    }
    // 循环方式,利用栈打印单链表
    public void display3(ListNode head) {
        if(this.head == null){
            return;
        }
        if(this.head.next == null){
            System.out.println(this.head.val + " ");
            return;
        }
        //吧引用类型 放到栈里
        Stack stack = new Stack<>();
        ListNode cur = this.head;
        while(cur != null){
            stack.push(cur);
            cur = cur.next;
        }
        //出栈打印
        while(! stack.empty()){
            ListNode ret = stack.pop();
            System.out.println(ret + " ");
        }
    }

五.概念区分

1. 栈、虚拟机栈、栈帧有什么区别呢？

栈 : 是一种先进后出的数据结构。

虚拟机栈 : 是JVM的一块内存空间。

栈帧 : 是在调用函数的过程当中，在Java虚拟机栈上开辟的一块内存。