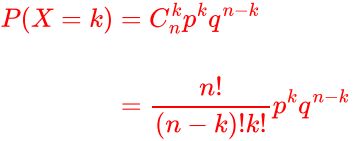21- 朴素贝叶斯 (NLP自然语言算法) (算法)

朴素贝叶斯要点

• 概率图模型算法往往应用于NLP自然语言处理领域。
• 根据文本内容判定 分类 。

•  概率密度公式：  

• 高斯朴素贝叶斯算法:

from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X_train,y_train)

• 伯努利分布朴素贝叶斯算法

from sklearn.naive_bayes import BernoulliNB
model = BernoulliNB()
model.fit(X_train,y_train)

• 多项式分布朴素贝叶斯表现

from sklearn.naive_bayes import MultinomialNB
model = MultinomialNB()
model.fit(X_train,y_train)

• 英文one-hot编码: jieba.lcut(str)

import jieba 
[i for i in jieba.lcut(s) if i not in [' ',',','.','!']]

• 数据去重:    result = np.unique(result)    # 去重
• TF-IDF的主要思想是：TF-IDF是一种用于信息检索与文本挖掘的常用加权技术，如果某个单词在一篇文章中出现的频率TF高，并且在其他文章中很少出现，则认为此词或者短语具有很好的类别区分能力，适合用来分类。
  • 词频 (TF) 是一词语出现的次数除以该文件的总词语数。假如一篇文件的总词语数是100个，而词语“Python”出现了5次，那么“Python”一词在该文件中的词频就是3/100=0.05。
  • 一个计算文件频率 (IDF) 的方法是文件集里包含的文件总数除以测定有多少份文件出现过“Python”一词。所以，如果“Python”一词在1000份文件出现过，而文件总数是10000000份的话，其逆向文件频率就是 lg(10000000 /1000)=4。最后的TF-IDF的分数为0.05 * 4=0.2。

---

1、概率图模型概述

概率图模型算法往往应用于NLP自然语言处理领域。
当然很多传统机器学习的算法也常用于 NLP 的任务。例如，用朴素贝叶斯进行文本分类、用 SVM 进行语义角色标注，虽然它们在某些 NLP 任务中都实现了很好的效果，但它们都相互独立， 没有形成体系。
随着近些年对智能推理和认知神经学的深入研究，人们对大脑和语言的内在机制了解得越来越多，也越来越能从更高层次上观察和认识自然语言，由此形成一套完整的算法体系。目前最流行的算法思想包含如下两大流派：

• 基于概率论和图论的概率图模型
• 基于人工神经网络的深度学习理论

2、贝叶斯

2.1、贝叶斯案例一
一个例子，现分别有 A、B 两个容器，在容器 A 里分别有 7 个红球和 3 个白球，在容器 B 里有 1 个红球和 9 个白球，现已知从这两个容器里任意抽出了一个球，且是红球，问这个红球是来自容器 A 的概率是多少?
2.2、贝叶斯案例二
例如：一座别墅在过去的 20 年里一共发生过 2 次被盗，别墅的主人有一条狗，狗平均每周晚上叫 3 次，在盗贼入侵时狗叫的概率被估计为 0.9，问题是：在狗叫的时候发生入侵的概率是多少？

3、朴素贝叶斯

举个例子，大学的时候，某男生经常去007自习室上晚自习，发现他喜欢的那个女生也常去那个自习室，心中窃喜，于是每天买点好吃的在那个自习室蹲点等她来，可是人家女生不一定每天都来，眼看天气渐渐炎热，自习室又不开空调，如果那个女生没去自习室，该男生也就不去，每次男生鼓足勇气说：“嘿，你明天还来不？”,“啊，不知道，看情况”。
然后该男生每天就把她去自习室与否以及一些其他情况做一下记录，用Y表示该女生是否去自习室，即Y={去，不去}，X是跟去自习室有关联的一系列条件，比如当天上了哪门主课，蹲点统计了一段时间后，该男生打算今天不再蹲点，而是先预测一下她会不会去，现在已经知道了今天上了常微分方程这门主课，于是计算P(Y=去|常微分方程)与P(Y=不去|常微分方程)，看哪个概率大，如果P(Y=去|常微分方程) >P(Y=不去|常微分方程)，那这个男生不管多热都屁颠屁颠去自习室了，否则就不去自习室受罪了。
P(Y=去|常微分方程)的计算可以通过贝叶斯公式进行计算，公式如下：

 后来他发现还有一些其他条件可以挖，比如当天星期几、当天的天气，统计了一段时间后，该男子一计算，发现不好算了，因为总结历史的公式：

这里n = 3，x(1)表示主课，x(2)表示天气，x(3)表示星期几，Y仍然是{去，不去}，现在主课有8门，天气有晴、雨、阴三种，那么总共需要估计的参数有8×3×7×2=336个，每天只能收集到一条数据，那么等凑齐336条数据，黄花菜都凉了，男生大呼不妙！
于是做了一个独立性假设，假设这些影响她去自习室的因素是独立互不相关的！
有了这个独立假设后，需要估计的参数就变为，(8+3+7)×2 = 36个了，而且每天收集的一条数据，可以提供3个参数，这样该男生就预测越来越准了！

4、朴素贝叶斯模型介绍

4.1、高斯分布朴素贝叶斯

高斯分布朴素贝叶斯 一一>正太分布

概率密度公式：

f(x) 表示事件的概率分布。

5.2、伯努利分布朴素贝叶斯

伯努利分布又叫做0-1分布，指一次随机试验，结果只有两种。也就是一个随机变量的取值只有0和1。记为: 0-1分布 或B(1,p)，其中 p 表示一次伯努利实验中结果为正或为1的概率。
假设你要生孩子，生男孩子概率p，生女孩纸概率1-p。
伯努利实验：例如，生一次孩子。
伯努利分布：生一次孩子，生男孩子概率为p,生女孩纸概率1-p，这个就是伯努利分布。

伯努利实验就是做一次服从伯努利概率分布的事件，它发生的可能性是p，不发生的可能性是1-p。
由伯努利分布延伸到二项分布，二项分布是多次伯努利分布实验的概率分布。
以抛硬币举例，在抛硬币事件当中，每一次抛硬币的结果是独立的，并且每次抛硬币正面朝上的概率是恒定的，所以单次抛硬币符合伯努利分布。我们假设硬币正面朝上的概率是p，那么反面朝上的概率是q=(1-p)。我们重复抛n次硬币，其中有k项正面朝上的事件，就是二项分布：

        

 5.3、多项式分布朴素贝叶斯

多项分布是在二项分布的基础上进一步的拓展。
以掷色子为例，在掷色子实验中可能出现的结局是：1,2,3,4,5,6（6标记为k，便于书写公式），分别记为变量，它们的概率分布分别是 。那么在n次实验的结果中，1出现 次、2出现 次、…、k 出现 次，这种事件的出现概率P有下面公式：

6、朴素贝叶斯模型使用

使用正太分布数据，鸢尾花作为示例（鸢尾花是自然界的植物，其自身特征数据是正态分布的~）

6.1、数据加载

import numpy as np
from sklearn import datasets
from sklearn.naive_bayes import GaussianNB # 高斯NB，Naive Bayes # navie 天真，朴素
from sklearn.model_selection import train_test_split
# 自然界中鸢尾花，自然属性，符合正态分布， 花萼长宽，花瓣长宽
X,y = datasets.load_iris(return_X_y=True)

6.2、高斯分布朴素贝叶斯表现

# 正太分布，属性
score = 0
model = GaussianNB()
for i in range(100):
    X_train,X_test,y_train,y_test = train_test_split(X,y)
    model.fit(X_train,y_train)
    score += model.score(X_test,y_test)/100
print('高斯朴素贝叶斯算法平均预测准确率是：',score)    # 0.9547368421052624

6.3、伯努利分布朴素贝叶斯表现

# 你想，我们的数据特征分布，是二项分布？？？
from sklearn.naive_bayes import BernoulliNB
score = 0
model = BernoulliNB()
for i in range(100):
    X_train,X_test,y_train,y_test = train_test_split(X,y)
    model.fit(X_train,y_train)
    score += model.score(X_test,y_test)/100
print('伯努利分布朴素贝叶斯算法平均预测准确率是：',score)   # 0.2694736842105264

6.4、多项式分布朴素贝叶斯表现

# 植物，数据，符合多项式分布
# 人身高：离散，极矮、矮、中等、高、特别高（满足多项分布）
# 多项分布 和 高斯分布，一定的类似
from sklearn.naive_bayes import MultinomialNB # 二项分布的延伸
score = 0
model = MultinomialNB()
for i in range(1000):
    X_train,X_test,y_train,y_test = train_test_split(X,y)
    model.fit(X_train,y_train)
    score += model.score(X_test,y_test)/1000
print('多项式分布朴素贝叶斯算法平均预测准确率是：',score)  # 0.8199473684210529

• 综上所述, 高斯分布效果较好

7、文本分类

文本分类的结构化方法就是 one-hot 表达模型。它是最直观，也是目前为止最常用的词表示方法，虽然越来越多的实践已经证明，这种模型存在局限性，但它仍在文本分类中得到广泛应用。
假设把语料库中的所有词都收集为一个词典 D，词典容纳了语料库中所有句子的词汇。
One-hot 方法就是把每个词表示为一个长长的向量。这个向量的维度是词典大小，其中绝大多数元素为 0，只有一个维度的值为 1。这个维度就代表了当前的词。

7.1、英文one-hot编码

文本一：My dog ate my homework；
文本二：My cat ate the fish；
文本三：Precious things are very few in the world,that is the reason there is only one you!

# jieba分词，中国人写的Python库
# 一句话，分成一个个词
import jieba   # pip install jieba
jieba.lcut('My dog ate my homework.')
''' ['My', ' ', 'dog', ' ', 'ate', ' ', 'my', ' ', 'homework', '.'] '''

data = ['My dog ate my homework.',
'My cat ate the fish.',
'Precision things are very few in the world,that is the reason there is only you!']
result = []
for s in data:
    result.extend([i for i in jieba.lcut(s) if i not in [' ',',','.','!']])
    
result = np.array(result)
result = np.unique(result) # 去重
result

7.2、中文one-hot编码

s1 = '喜欢上一个人'
s2 = '尼姑亲吻了和尚的嘴唇'
s3 = '老师你教的都是没有的东西'

import jieba
import numpy as np
data = ['喜欢上一个人','尼姑亲吻了和尚的嘴唇','老师你教的都是没有的东西']
result = []
for s in data:
    result.extend([i for i in jieba.lcut(s)])
result = np.array(result)
result = np.unique(result)
print(result)
for s in data:
    word_embedding = [(i == result).astype(np.int8) for i in jieba.lcut(s
                                                  ) if i not in [' ', ',','.','!']]
print(np.array(word_embedding))
'''['一个' '上' '东西' '了' '亲吻' '人' '你' '和尚' '喜欢' '嘴唇' '尼姑' '教' '是' 
'没有' '的' '老师' '都']
[[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0]
 [0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
 [0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0]
 [0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]'''

7.3、TF-IDF

7.3.1、词频-逆向文件频率介绍
TF-IDF（term frequency–inverse document frequency，词频-逆向文件频率）是一种用于信息检索（information retrieval）与文本挖掘（text mining）的常用加权技术。
TF-IDF是一种统计方法，用以评估某字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。
TF-IDF的主要思想是：如果某个单词在一篇文章中出现的频率TF高，并且在其他文章中很少出现，则认为此词或者短语具有很好的类别区分能力，适合用来分类。
7.3.2、词频TF计算
词频（TF）表示词条（关键字）在文本中出现的频率。
        
7.3.3、逆向文件频率IDF计算
逆向文件频率 (IDF) ：某一特定词语的IDF，可以由总文件数目除以包含该词语的文件的数目，再将得到的商取对数得到。
如果包含词条t的文档越少, IDF越大，则说明词条具有很好的类别区分能力。

        
7.3.4、TF-IDF计算
某一特定文件内的高词语频率，以及该词语在整个文件集合中的低文件频率，可以产生出高权重的TF-IDF。因此，TF-IDF倾向于过滤掉常见的词语，保留重要的词语。

        
7.3.5、TF-IDF算例演示
有很多不同的数学公式可以用来计算TF-IDF。词频 (TF) 是一词语出现的次数除以该文件的总词语数。假如一篇文件的总词语数是100个，而词语“Python”出现了5次，那么“Python”一词在该文件中的词频就是3/100=0.05。一个计算文件频率 (IDF) 的方法是文件集里包含的文件总数除以测定有多少份文件出现过“Python”一词。所以，如果“Python”一词在1000份文件出现过，而文件总数是10000000份的话，其逆向文件频率就是 lg(10000000 /1000)=4。最后的TF-IDF的分数为0.05 * 4=0.2。

import numpy as np
from sklearn.feature_extraction.text import CountVectorizer # 统计计数
from sklearn.feature_extraction.text import TfidfTransformer

data = np.array(['政治 历史 地理 语文 政治', 'Python 英语 语文 英语 数学'])
# 统计是词频
cv = CountVectorizer() 
print(cv.fit_transform(data))
cv.vocabulary_  
# {'政治': 3, '历史': 1, '地理': 2, '语文': 6, 'python': 0, '英语': 5, '数学': 4}

result = cv.fit_transform(data)
result.toarray()
'''array([[0, 1, 1, 2, 0, 0, 1],
       [1, 0, 0, 0, 1, 2, 1]], dtype=int64)'''

• tf-idf权值计算,  对样本进行转换

tfidf = TfidfTransformer()
tfidf_result = tfidf.fit_transform(result)
tfidf_result.toarray()
'''array([[0. , 0.39204401, 0.39204401, 0.78408803, 0. , 0. , 0.27894255],
          [0.39204401, 0. , 0. , 0. , 0.39204401, 0.78408803, 0.27894255]])'''

8、垃圾短信分类项目实战

8.1、数据加载与介绍

import pandas as pd
from sklearn.naive_bayes import GaussianNB,BernoulliNB,MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer,TfidfTransformer
messages = pd.read_csv('./data/messages.csv',sep = '\t',header=None)
messages.rename({0:'label',1:'message'},axis = 1,inplace = True)
messages     # 0表示短信类别；1表示短信内容

 8.2、文本数据处理

cv = CountVectorizer()   # stop-words 停用词，英文中的标点符号，对分类作用不大 # 量化
# 词向量
X = cv.fit_transform(messages['message'])   # 向量化，原数据是单词（计算机无法建模）
X   # 5572样本，8713 多少个非重复的词

稀松矩阵介绍

a = np.random.randint(0,10,size = (100000,5))
a[a > 3] = 0 # 大部分都是0
print(a)     # 常规矩阵，0表示没有，但是占着位置，占据内存
np.savez('稠密矩阵.npz',a)  # 20.3kb

# 使用scipy中方法，转换成稀松矩阵，0不算数，不统计
from scipy import sparse
s = sparse.csr_matrix(a)
sparse.save_npz('稀松矩阵.npz',s)   # 3.68kb

TF-IDF转换

from sklearn.feature_extraction.text import TfidfVectorizer
tf_idf = TfidfTransformer()
X2 = tf_idf.fit_transform(X) # 稀松矩阵
X_train,X_test,y_train,y_test = train_test_split(X2,y)
display(X_train,X_test)
'''<4179x8713 sparse matrix of type ''
   <1393x8713 sparse matrix of type ''''

tf_idf2 = TfidfVectorizer()
# TfidfVectorizer 相当于 先使用CountVectorizer，然后使用TfidfTransformer
X3 = tf_idf2.fit_transform(messages['message'])
X3  '''<5572x8713 sparse matrix of type '' '''

8.3、数据建模评估

高斯朴素贝叶斯

%%time   # 1 s
gNB = GaussianNB()
gNB.fit(X_train.toarray(),y_train)
gNB.score(X_test.toarray(),y_test)   # 0.8966259870782484

伯努利

%%time   # 31.2 ms
# 人使用的语言，更加符合二项分布
bNB = BernoulliNB() # 传入数据是，稀松矩阵
bNB.fit(X_train,y_train)
bNB.score(X_test,y_test)   # 0.9770279971284996

多项式分布

%%time   # 15.6 ms
mNB = MultinomialNB()
mNB.fit(X_train,y_train)
mNB.score(X_test,y_test)   # 0.9619526202440776

8.4、构建新短信预测

X_test = ['Your free ringtone is waiting to be collected. Simply text the d "MIX" to 85069 to verify.I see the letter B on my car Please call now 08000930705 for delivery tomorrow',
          'Precious things are very few in the world,that is the reason there is only one you',
          "GENT! We are trying to contact you. Last weekends draw shows that you won a £1000 prize GUARANTEED. U don't know how stubborn I am. Congrats! 1 year special cinema pass for 2 is yours.",
          'Congrats! 1 year special cinema pass for 2 is yours. call 09061209465 now! C Suprman V, Matrix3, StarWars3, etc all 4 FREE! bx420-ip4-5we. 150pm. Dont miss out!']
X_test_tf_idf = tf_idf.transform(cv.transform(X_test))
bNB.predict(X_test_tf_idf)  # array(['spam', 'ham', 'spam', 'spam'], dtype='

9、新闻类别划分

9.1、加载数据（联网国外下载）

from sklearn import datasets
from sklearn.naive_bayes import GaussianNB,BernoulliNB,MultinomialNB
# countVectorizer词频
# tf-idf term frequency（词频） inverse document frequency（你文本词频） + 权重
from sklearn.feature_extraction.text import TfidfVectorizer,ENGLISH_STOP_WORDS  
from sklearn.model_selection import train_test_split
news = datasets.fetch_20newsgroups(data_home='./data/',subset='all')
news['target_names']   # target 目标

        

查看部分数据

# 加载一部分数据
news = datasets.fetch_20newsgroups(data_home='./data/',subset='all',
                                   remove= ('headers', 'footers', 'quotes'),
                                   categories = ['rec.motorcycles',
                                   'rec.sport.hockey','talk.politics.guns'])
print(len(news['target']))   # 2905
print(news['data'][0])

9.2、文本数据转换

tf_idf = TfidfVectorizer()

X = tf_idf.fit_transform(news['data'])
# X_train,X_test依然是 稀松矩阵
X_train,X_test,y_train,y_test = train_test_split(X,news['target'])

9.3、数据建模

%%time
gNB = GaussianNB()
gNB.fit(X_train.toarray(),y_train)
gNB.score(X_test.toarray(),y_test)   # 0.8665749656121046

%%time
bNB = BernoulliNB() # 二项分布
bNB.fit(X_train,y_train)
bNB.score(X_test,y_test)   # 0.7372764786795049

%%time
mNB = MultinomialNB()
mNB.fit(X_train,y_train)
mNB.score(X_test,y_test)   # 0.9092159559834938

10、贝叶斯网络

10.1、朴素贝叶斯与贝叶斯网络

朴素贝叶斯可以看做是贝叶斯网络的特殊情况：即该网络中无边，各个节点都是独立的（前提是独立性假设）。那么，当朴素贝叶斯中的假设：独立同分布不成立时，应该如何解决呢？可以使用贝叶斯网络。贝叶斯网络借助有向无环图来刻画属性之间的依赖关系，并使用条件概率表来描述属性的联合概率分布。

        

10.2、贝叶斯网络定义

贝叶斯网络(Bayesian network)，又称信念网络(Belief Network)，或有向无环图模型(directed acyclic graphicalmodel)，是一种概率图模型，于1985年由Judea Pearl首先提出。它是一种模拟人类推理过程中因果关系的不确定性处理模型，其网络拓朴结构是一个有向无环图(DAG)。

10.3、贝叶斯网络三种结构

形式一：head-to-head :

        

上图概率公式如下：P(a,b,c) = P(a) * P(b) * P(c|a,b)。
在 c 未知的条件下，a、b被阻断(blocked)，是独立的，称之为head-to-head条件独立。也就是a和b符合独立性假设。

形式二：tail-to-tail

        

1. 在 c 未知的时候，有：P(a,b,c)=P(c) * P(a|c) * P(b|c)，此时，没法得出 P(a,b) = P(a) * P(b)，
即 c 未知时，a、b 不独立。
2. 在 c 已知的时候，有：P(a,b|c)=P(a,b,c) / P(c)，然后将 P(a,b,c)=P(c) * P(a|c) * P(b|c)带入
式子中，得到：P(a,b|c)=P(a,b,c) / P(c) = P(c) * P(a|c) * P(b|c) / P(c) = P(a|c) * P(b|c)，即 c
已知时，a、b 独立。

形式三：head-to-tail

        

 1. c 未知时，有：P(a,b,c)=P(a) * P(c|a) * P(b|c)，但无法推出 P(a,b) = P(a) * P(b)，即 c 未知
时，a、b 不独立。
2. c 已知时，有：P(a,b|c)=P(a,b,c) / P(c)，且根据 P(a,c) = P(a) * P(c|a) = P(c) * P(a|c)，可化
简得到：
P(a,b|c) = P(a,b,c) / P(c)
              = P(a) * P(c|a) * P(b|c) / P(c)
              = P(a,c) * P(b|c) / P(c)
              = P(a|c) * P(b|c)
所以，在 c 给定的条件下，a，b 被阻断(blocked)，是独立的，称之为 head-to-tail
条件独立。朴素贝叶斯可以看做是贝叶斯网络的特殊情况：即该网络中无边，各个节点都是独立的。 朴素贝叶斯朴素在哪里呢？ 一个特征出现的概率与其他特征（条件）独立！

10.4、贝叶斯网络实例

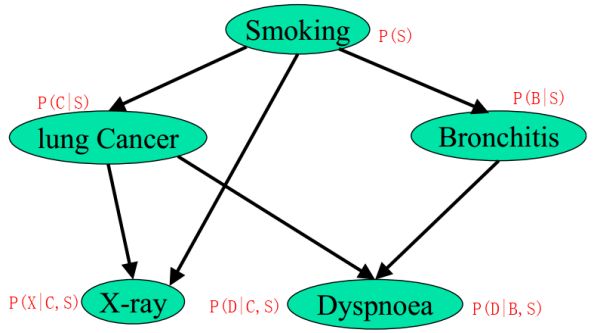
有如下贝叶斯网络：

        

其中，各个单词、表达式表示的含义如下：

• smoking 表示吸烟，其概率用 P(S) 表示，lung Cancer 表示肺癌，一个人在吸烟的情况下得肺癌的概率用P(C|S) 表示，X-ray 表示需要照医学上的 X 光，肺癌可能会导致需要照 X 光，吸烟也有可能会导致需要照 X 光（所以 smoking 也是 X-ray 的一个因素），所以，因吸烟且得肺癌而需要照X光的概率用 P(X|C,S) 表示。
• Bronchitis 表示支气管炎，一个人在吸烟的情况下得支气管炎的概率用 P(B|S)，Dyspnoea 表示呼吸困难，支气管炎可能会导致呼吸困难，肺癌也有可能会导致呼吸困难（所以 lung Cancer 也是Dyspnoea的一个因素），因吸烟且得了支气管炎导致呼吸困难的概率用P(D|S,B)表示。

lung Cancer 简记为 C，Bronchitis 简记为 B，Dyspnoea 简记为 D，且 C = 0 表示 lung Cancer 不发生的概率，C = 1表示 lung Cancer 发生的概率，其他含义类似。

10.5、概率图模型

概率图模型是一类用图形模式表达基于概率相关关系的模型的总称。概率图模型结合概率论与图论的知识，利用图来表示与模型有关的变量的联合概率分布。近10年它已成为不确定性推理的研究热点，在人工智能、机器学习和计算机视觉等领域有广阔的应用前景。
根据是否是有向图，可以分为有向图模型和无向图模型。
有向图模型（又称为贝叶斯网络），例如：隐马尔科夫模型（Hidden Markov Model，HMM）
无向图模型（又称为马尔科夫网络），例如：条件随机场（Conditional Random Fields，CRF）
后面课程中会，进行介绍说明。