LeetCode分类刷题(九):二叉树(Tree)(2)
树是一种比较重要的数据结构,尤其是二叉树。二叉树是一种特殊的树,在二叉树中每个节点最多有两个子节点,一般称为左子节点和右子节点(或左孩子和右孩子),并且二叉树的子树有左右之分,其次序不能任意颠倒。二叉树是递归定义的,因此,与二叉树有关的题目基本都可以用递归思想解决,当然有些题目非递归解法也应该掌握,如非递归遍历节点等等。本文努力对二叉树相关题目做一个较全的整理总结,希望对找工作的同学有所帮助。
二叉树节点定义如下:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};LeetCode中关于二叉树的进阶题目有以下三种类型题:
(1)二叉树之二叉搜索树(中序遍历)相关题目:
(2)二叉树之路径和(后序遍历)相关题目:
(3)二叉树之面试进阶相关题目:
(1)二叉树之二叉搜索树(中序遍历)相关题目:
98. Validate Binary Search Tree
- Given a binary tree, determine if it is a valid binary search tree (BST).
- 题目要求:验证二叉搜索树。
- 题目分析:使用中序遍历来做,这种方法思路很直接,通过中序遍历将所有的节点值存到一个数组里,然后再来判断这个数组是不是有序的。
- 题目解答:
class Solution {
public:
bool isValidBST(TreeNode* root) {
if(root == nullptr) return true;
stack stk;
TreeNode *cur = root, *pre = nullptr;
while(cur || stk.size()){
if(cur){
stk.push(cur);
cur = cur->left;
}else{
cur = stk.top();
stk.pop();
if(pre != nullptr && pre->val >= cur->val) return false;
pre = cur;
cur = cur->right;
}
}
return true;
}
}; 230. Kth Smallest Element in a BST
- Given a binary search tree, write a function
kthSmallestto find the kth smallest element in it. - 题目要求:求二叉搜索树中的第K小的元素。
- 题目分析:非递归的方法,中序遍历最先遍历到的是最小的结点,那么我们只要用一个计数器,每遍历一个结点,计数器自增1,当计数器到达k时,返回当前结点值即可。
- 题目解答:
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
if(root == nullptr) return 0;
stack stk;
TreeNode *cur = root;
while(cur || stk.size()){
if(cur){
stk.push(cur);
cur = cur->left;
}else{
cur = stk.top();
stk.pop();
if(--k == 0) break;
cur = cur->right;
}
}
return cur->val;
}
}; 108. Convert Sorted Array to Binary Search Tree
- Given an array where elements are sorted in ascending order, convert it to a height balanced BST.
- 题目要求:将有序数组转为二叉搜索树。
- 题目分析:所谓二叉搜索树,是一种始终满足左<根<右的特性,如果将二叉搜索树按中序遍历的话,得到的就是一个有序数组了。那么反过来,我们可以得知,根节点应该是有序数组的中间点,从中间点分开为左右两个有序数组,在分别找出其中间点作为原中间点的左右两个子节点,这不就是是二分查找法的核心思想么。所以这道题考的就是二分查找法。
- 题目解答:
class Solution {
public:
TreeNode* sortedArrayToBST(vector& nums) {
return helper(nums, 0, nums.size() - 1);
}
TreeNode* helper(vector& nums, int low, int high){
if(low > high) return nullptr;
int mid = (low + high) / 2;
TreeNode *root = new TreeNode(nums[mid]);
root->left = helper(nums, low, mid - 1);
root->right = helper(nums, mid + 1, high);
return root;
}
}; 109. Convert Sorted List to Binary Search Tree
- Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.
- 题目要求:这道题是要求把有序链表转为二叉搜索树。
- 题目分析:由于二分查找法每次需要找到中点,而链表的查找中间点可以通过快慢指针来操作。找到中点后,要以中点的值建立一个数的根节点,然后需要把原链表断开,分为前后两个链表,都不能包含原中节点,然后再分别对这两个链表递归调用原函数,分别连上左右子节点即可。
- 题目解答:
class Solution {
public:
TreeNode* sortedListToBST(ListNode* head) {
return helper(head, nullptr);
}
TreeNode* helper(ListNode *head, ListNode *tail){
if(head == tail) return nullptr;
ListNode *fast = head, *slow = head;
while(fast != tail && fast->next != tail){
slow = slow->next;
fast = fast->next->next;
}
TreeNode *root = new TreeNode(slow->val);
root->left = helper(head, slow);
root->right = helper(slow->next, tail);
return root;
}
};96. Unique Binary Search Trees
- Given n, how many structurally unique BST's (binary search trees) that store values 1 ... n?
- 题目要求:给出n,包含1~n这些节点可以形成多少个不同的BST(二叉查找树)?
- 题目分析:把n = 0 时赋为1,因为空树也算一种二叉搜索树,那么n = 1时的情况可以看做是其左子树个数乘以右子树的个数,左右字数都是空树,所以1乘1还是1。那么n = 2时,由于1和2都可以为跟,分别算出来,再把它们加起来即可。n = 2的情况可由下面式子算出:dp[2] = dp[0] * dp[1](1为根的情况)+ dp[1] * dp[0](2为根的情况);同理可写出 n = 3 的计算方法:dp[3] = dp[0] * dp[2](1为根的情况)+ dp[1] * dp[1](2为根的情况)+ dp[2] * dp[0](3为根的情况);由此可以得出卡塔兰数列的递推式为:
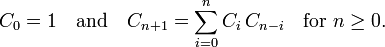
- 题目解答:
class Solution {
public:
int numTrees(int n) {
int dp[n + 1] = {0};
dp[0] = 1;
dp[1] = 1;
for(int i = 2; i <= n; i++){
for(int j = 0; j < i; j++){
dp[i] += dp[j] * dp[i - j - 1];
}
}
return dp[n];
}
};(2)二叉树之路径和(后序遍历)相关题目:
112. Path Sum
- Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.
- 题目要求:题目意思是给了一个二叉树,每个节点对应一个值,同时给了一个指定的树。 然后请问是否有一条从根节点开始,到叶节点的路径,其和正好等于那个值。
- 题目分析:这道求二叉树的路径需要用深度优先算法DFS的思想来遍历每一条完整的路径,也就是利用递归不停找子节点的左右子节点,而调用递归函数的参数只有当前节点和sum值。首先,如果输入的是一个空节点,则直接返回false,如果如果输入的只有一个根节点,则比较当前根节点的值和参数sum值是否相同,若相同,返回true,否则false。 这个条件也是递归的终止条件。下面我们就要开始递归了,由于函数的返回值是Ture/False,我们可以同时两个方向一起递归,中间用或||连接,只要有一个是True,整个结果就是True。递归左右节点时,这时候的sum值应该是原sum值减去当前节点的值。
- 题目解答:
class Solution {
public:
bool hasPathSum(TreeNode* root, int sum) {
if(root == nullptr) return false;
if(root->left == nullptr && root->right == nullptr && sum == root->val) return true;
return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);
}
};113. Path Sum II
- Given a binary tree and a sum, find all root-to-leaf paths where each path's sum equals the given sum.
- 题目要求:这道二叉树路径之和在之前的基础上又需要找出路径。
- 题目分析:需要用深度优先搜索DFS,只不过数据结构相对复杂一点,需要用到二维的vector,而且每当DFS搜索到新节点时,都要保存该节点。而且每当找出一条路径之后,都将这个保存为一维vector的路径保存到最终结果二位vector中。并且,每当DFS搜索到子节点,发现不是路径和时,返回上一个结点时,需要把该节点从一维vector中移除。
- 题目解答:
class Solution {
public:
vector> pathSum(TreeNode* root, int sum) {
vector> res;
vector path;
findPaths(root, sum, res, path);
return res;
}
void findPaths(TreeNode* root, int sum, vector>& paths, vector& path){
if(root == nullptr) return;
path.push_back(root->val);
if(root->left == nullptr && root->right == nullptr && sum == root->val) paths.push_back(path);
findPaths(root->left, sum - root->val, paths, path);
findPaths(root->right, sum - root->val, paths, path);
path.pop_back();
}
}; 437. Path Sum III
- You are given a binary tree in which each node contains an integer value. Find the number of paths that sum to a given value.
- 题目要求:这道题让我们求二叉树的路径的和等于一个给定值,说明了这条路径不必要从根节点开始,可以是中间的任意一段,而且二叉树的节点值也是有正有负。
- 题目分析:利用深度遍历解决问题。
- 题目解答:
class Solution {
public:
int pathSum(TreeNode* root, int sum) {
if(root == nullptr) return 0;
return findPath(root, sum) + pathSum(root->left, sum) + pathSum(root->right, sum);
}
int findPath(TreeNode* root, int sum){
int res = 0;
if(root == nullptr) return res;
if(root->val == sum) res++;
res += findPath(root->left, sum - root->val);
res += findPath(root->right, sum - root->val);
return res;
}
};129. Sum Root to Leaf Numbers
- Given a binary tree containing digits from
0-9only, each root-to-leaf path could represent a number. - 题目要求:这道求根到叶节点数字之和。
- 题目分析:利用DFS递归来解,这道题由于不是单纯的把各个节点的数字相加,而是每到一个新的数字,要把原来的数字扩大10倍之后再相加。
- 题目解答:
class Solution {
public:
int sumNumbers(TreeNode* root) {
return getSum(root, 0);
}
int getSum(TreeNode* root, int s){
if(root == nullptr) return 0;
if(root->left == nullptr && root->right == nullptr) return 10*s+root->val;
return getSum(root->left, 10*s+root->val) + getSum(root->right, 10*s+root->val);
}
};257. Binary Tree Paths
- Given a binary tree, return all root-to-leaf paths.
- 题目要求:这道题给我们一个二叉树,让我们返回所有根到叶节点的路径。
- 题目分析:树的题目,十有八九都是递归,而递归的核心就是不停的DFS到叶结点,然后在回溯回去。在递归函数中,当我们遇到叶结点的时候,即没有左右子结点,那么此时一条完整的路径已经形成了,我们加上当前的叶结点后存入结果res中,然后回溯。注意这里结果res需要reference,而out是不需要引用的,不然回溯回去还要删除新添加的结点,很麻烦。为了减少判断空结点的步骤,我们在调用递归函数之前都检验一下非空即可。
- 题目解答:
class Solution {
public:
vector binaryTreePaths(TreeNode* root) {
vector res;
if(root) helper(root, "", res);
return res;
}
void helper(TreeNode *node, string out, vector& res){
if(node->left == nullptr && node->right == nullptr) res.push_back(out + to_string(node->val));
if(node->left) helper(node->left, out + to_string(node->val) + "->", res);
if(node->right) helper(node->right, out + to_string(node->val) + "->", res);
}
}; (3)二叉树之面试进阶相关题目:
105. Construct Binary Tree from Preorder and Inorder
- Given preorder and inorder traversal of a tree, construct the binary tree.
- 题目要求:这道题要求用先序和中序遍历来建立二叉树。
- 题目分析:针对这道题,由于先序的顺序的第一个肯定是根,所以原二叉树的根节点可以知道,题目中给了一个很关键的条件就是树中没有相同元素,有了这个条件我们就可以在中序遍历中也定位出根节点的位置,并以根节点的位置将中序遍历拆分为左右两个部分,分别对其递归调用原函数。
- 题目解答:
class Solution {
public:
TreeNode* buildTree(vector& preorder, vector& inorder) {
return helper(preorder, 0, preorder.size()-1, inorder, 0, inorder.size()-1);
}
TreeNode* helper(vector& preorder, int beg1, int end1, vector& inorder, int beg2, int end2){
if(beg1 > end1) return nullptr;
TreeNode* root = new TreeNode(preorder[beg1]);
int i = beg2;
for(; i <= end2; i++)
if(preorder[beg1] == inorder[i]) break;
int leftnum = i - beg2;
root->left = helper(preorder, beg1+1, beg1+leftnum, inorder, beg2, beg2+leftnum-1);
root->right = helper(preorder, beg1+leftnum+1, end1, inorder, beg2+leftnum+1, end2);
return root;
}
}; 106. Construct Binary Tree from Inorder and Postorder Traversal
- Given inorder and postorder traversal of a tree, construct the binary tree.
- 题目要求:这道题要求用后序和中序遍历来建立二叉树。
- 题目分析:针对这道题,由于后序的顺序的最后一个肯定是根,所以原二叉树的根节点可以知道,题目中给了一个很关键的条件就是树中没有相同元素,有了这个条件我们就可以在中序遍历中也定位出根节点的位置,并以根节点的位置将中序遍历拆分为左右两个部分,分别对其递归调用原函数。
- 题目解答:
class Solution {
public:
TreeNode* buildTree(vector& inorder, vector& postorder) {
return helper(postorder, 0, postorder.size()-1, inorder, 0, inorder.size()-1);
}
TreeNode* helper(vector& postorder, int beg1, int end1, vector& inorder, int beg2, int end2){
if(beg1 > end1) return nullptr;
TreeNode* root = new TreeNode(postorder[end1]);
int i = beg2;
for(; i <= end2; i++)
if(postorder[end1] == inorder[i]) break;
int leftnum = i - beg2;
root->left = helper(postorder, beg1, beg1+leftnum - 1, inorder, beg2, beg2+leftnum-1);
root->right = helper(postorder, beg1+leftnum, end1 -1, inorder, beg2+leftnum+1, end2);
return root;
}
}; 235. Lowest Common Ancestor of a Binary Search Tree
- Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
- 题目要求:这道题让我们求二叉搜索树的最小共同父节点。
- 题目分析:这道题我们可以用递归来求解,我们首先来看题目中给的例子,由于二叉搜索树的特点是左<根<右,所以根节点的值一直都是中间值,大于左子树的所有节点值,小于右子树的所有节点值,那么我们可以做如下的判断,如果根节点的值大于p和q之间的较大值,说明p和q都在左子树中,那么此时我们就进入根节点的左子节点继续递归,如果根节点小于p和q之间的较小值,说明p和q都在右子树中,那么此时我们就进入根节点的右子节点继续递归,如果都不是,则说明当前根节点就是最小共同父节点,直接返回即可。
- 题目解答:
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(p->val < root->val && q->val < root->val)
return lowestCommonAncestor(root->left, p, q);
if(p->val > root->val && q->val > root->val)
return lowestCommonAncestor(root->right, p, q);
return root;
}
};236. Lowest Common Ancestor of a Binary Tree
- Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
- 题目要求:求二叉树的最小共同父节点。
- 题目分析:我们仍然可以用递归来解决,递归寻找两个带查询LCA的节点p和q,当找到后,返回给它们的父亲。如果某个节点的左右子树分别包括这两个节点,那么这个节点必然是所求的解,返回该节点。否则,返回左或者右子树(哪个包含p或者q的就返回哪个)。
- 题目解答:
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == nullptr || root == p || root == q) return root;
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if(left && right) return root;
return left ? left : right;
}
};如果各位看官们,大神们发现了任何错误,或是代码无法通过OJ,或是有更好的解法,或是有任何疑问,意见和建议的话,请一定要在帖子下面评论区留言告知博主啊,多谢多谢,祝大家刷得愉快,刷得精彩,刷出美好未来~