自注意力机制(Self-Attention):从Seq2Seq模型到一般RNN模型
1. 前言
本文讲解自注意力机制(Self-Attention)。
本人全部文章请参见:博客文章导航目录
本文归属于:自然语言处理系列
本系列实践代码请参见:我的GitHub
前文:注意力机制(Attention):Seq2Seq模型的改进
后文:Attention is all you need:剥离RNN,保留Attention
2. 自注意力机制(Self-Attention)
Seq2Seq模型一般有两个RNN网络,一个为Encoder,另一个为Decoder。Attention用于改进Seq2Seq模型,解决RNN遗忘问题。
Self-Attention也叫做Intra-Attention,与Attention非常类似。Self-Attention不局限于Seq2Seq模型,可以用在任何RNN上,Self-Attention可改进一般RNN模型,解决一般RNN模型遗忘问题。实验证明Self-Attention对多种机器学习和自然语言处理的任务都有帮助。
2.1 SimpleRNN + Self-Attention
根据简单循环神经网络(Simple RNN)原理与实战一文可知,在不使用Self-Attention的情况下,Simple RNN通过如下公式更新状态:
h t + 1 = t a n h ( A ⋅ [ h t x t + 1 ] + b ) ( 1 ) h_{t+1}=tanh\big(A \cdot {h_t\brack x_{t+1}}+b\big)~~~~~~~~~~~~~~~~~~~~~~~~~~~(1) ht+1=tanh(A⋅[xt+1ht]+b) (1)
为了更方便说明Self-Attention原理,设当前时刻为 t t t时刻,下一时刻为 t + 1 t+1 t+1时刻。而不采用当前时刻为 t − 1 t-1 t−1时刻,下一时刻为 t t t时刻这种更常见的设定。
使用Self-Attention + SimpleRNN,将状态向量 h t h_t ht更新为 h t + 1 h_{t+1} ht+1之前需要计算当前状态 h t h_t ht与 h i , ( i = 0 ∼ t ) h_i, (i=0\sim t) hi,(i=0∼t)的相关性(权重) α t 0 , α t 1 , α t 2 , ⋯ , α t t \alpha_{t0},\alpha_{t1},\alpha_{t2},\cdots,\alpha_{tt} αt0,αt1,αt2,⋯,αtt。
α t i = a l i g n ( h i , h t ) ( 2 ) \alpha_{ti}=align(h_i,h_t)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(2) αti=align(hi,ht) (2)
α t i , ( i = 0 ∼ t ) \alpha_{ti},(i=0\sim t) αti,(i=0∼t)均是介于 0 ∼ 1 0\sim 1 0∼1之间的实数, ∑ i = 0 t α t i = 1 \sum_{i=0}^t\alpha_{ti}=1 ∑i=0tαti=1。
得到 h t h_t ht与SimpleRNN t t t时刻及之前所有时刻的状态 h 0 , h 1 , h 2 , ⋯ , h t h_0,h_1,h_2,\cdots,h_t h0,h1,h2,⋯,ht对应的权重 α t 0 , α t 1 , α t 2 , ⋯ , α t t \alpha_{t0},\alpha_{t1},\alpha_{t2},\cdots,\alpha_{tt} αt0,αt1,αt2,⋯,αtt之后,可以对SimpleRNN当前时刻 t t t及之前所有时刻的状态向量求加权平均,得到Context Vector,记为 c t c_t ct, c t = α t 0 h 0 + α t 1 h 1 + α t 2 h 2 + ⋯ + α t t h t c_t=\alpha_{t0}h_0+\alpha_{t1}h_1+\alpha_{t2}h_2+\cdots+\alpha_{tt}h_t ct=αt0h0+αt1h1+αt2h2+⋯+αttht。
得到Context Vector之后,通过如下公式更新状态:
h t + 1 = t a n h ( A ⋅ [ x t + 1 c t ] + b ) ( 3 ) h_{t+1}=tanh\big(A \cdot {x_{t+1}\brack c_t}+b\big)~~~~~~~~~~~~~~~~~~~~~~~~~~~(3) ht+1=tanh(A⋅[ctxt+1]+b) (3)
或
h t + 1 = t a n h ( A ⋅ [ h t x t + 1 c t ] + b ) ( 4 ) h_{t+1}=tanh\Big(A\cdot \begin{bmatrix} h_t\\ x_{t+1}\\ c_t \end{bmatrix} +b\Big)~~~~~~~~~~~~~~~~~~~~~~~~~~~(4) ht+1=tanh(A⋅⎣⎡htxt+1ct⎦⎤+b) (4)
c t c_t ct是 t t t时刻及之前所有时刻状态 h 0 , h 1 , h 2 , ⋯ , h t h_0, h_1, h_2, \cdots, h_t h0,h1,h2,⋯,ht的加权平均,即在将状态 h t h_t ht更新为 h t + 1 h_{t+1} ht+1之前,Self-Attention会查看之前所有状态,因此不会遗忘之前的信息。
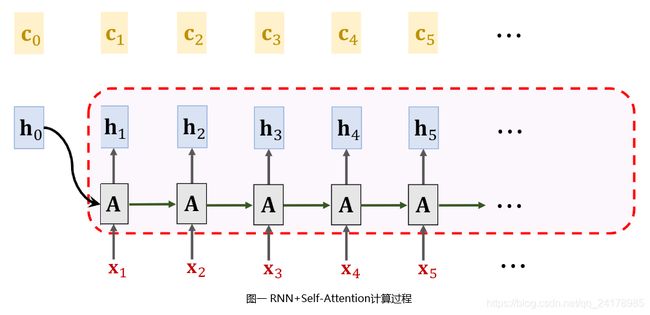
使用Self-Attention + SimpleRNN,状态更新过程如上图所示。初始时状态向量为 h 0 h_0 h0,Context Vector为 c 0 c_0 c0,一般均为全零向量,根据公式(3)或(4)可将状态 h 0 h_0 h0更新为 h 1 h_1 h1。再计算 c 1 c_1 c1,然后根据公式(3)或(4)将状态 h 1 h_1 h1更新为 h 2 h_2 h2。再计算 c 2 c_2 c2,然后根据公式(3)或(4)将状态 h 2 h_2 h2更新为 h 3 h_3 h3。不断重复该过程,计算新的Context Vector,然后生成新的状态向量,直至读取完整个输入序列。
计算Context Vector之前计算当前状态 h t h_t ht与 h i , ( i = 0 ∼ t ) h_i, (i=0\sim t) hi,(i=0∼t)的相关性(权重)方法与上文注意力机制(Attention):Seq2Seq模型的改进【3.2 权重计算方法】部分中所述方法一致。
2.2 权重的实际意义
如下图所示,Self-Attention + RNN从左往右读取一句话,红色单词为当前输入,高亮标注单词为权重 α \alpha α比较大的位置。权重表明了前文中最相关词的位置,即 α \alpha α表明了当前的输入与前文哪些词相关性较大。

3. 参考资料链接
- https://aclanthology.org/D16-1053.pdf
- https://www.youtube.com/watch?v=Vr4UNt7X6Gw&list=PLvOO0btloRnuTUGN4XqO85eKPeFSZsEqK&index=9