MATLAB学习笔记5：绘图基础与数据可视化（上）

阅读前请注意：

1. 该学习笔记是华中师范大学HelloWorld程序设计协会2021年寒假MATLAB培训的学习记录，是基于培训课堂内容的总结归纳、拓展阅读。博客内容由 @K2SO4钾 撰写、编辑，发布于 @K2SO4钾 的个人投稿与华中师范大学HelloWorld程序设计协会CSDN官方账号 @CCNU_HelloWorld 。注意，如需转载需得到作者 @K2SO4钾 的同意与授权！

2. 学习笔记基于 《MATLAB R2018a完全自学一本通》(刘浩, 韩晶) ¹ ，笔记中增加了很多程序示例和笔者个人的思考。学习笔记面向刚接触MATLAB的新手，内容偏基础。学习前请自行下载安装MATLAB。笔记中示例用MATLAB版本为MATLAB R2019a。

3. 请谅解笔记可能会出现的错误，欢迎指正讨论；由于MATLAB更新导致的旧代码无法使用的情况，也欢迎讨论交流。

5.0 MATLAB笔记：传送门汇总

5.0.1 MATLAB学习笔记：传送门汇总

MATLAB学习笔记0：学习须知

MATLAB学习笔记1：MATLAB概述

MATLAB学习笔记2：MATLAB基础知识（上）

MATLAB学习笔记3：MATLAB编程基础（前半）

MATLAB学习笔记3：MATLAB编程基础（后半）

5.0.2 MATLAB拓展学习：传送门汇总

MATLAB拓展学习T1：匿名函数和内联函数

MATLAB拓展学习T2：程序性能优化技术

MATLAB拓展学习T3：histogram函数详解

MATLAB拓展学习T4：数据导入

5.0.3 MATLAB专题博客：传送门汇总

MATLAB-S1：元胞自动机原理及MATLAB实现

MATLAB-S2：图像处理技术

5.0.4 MATLAB应用实例：传送门汇总

MATLAB应用实例：Floyd算法

MATLAB应用实例：简单数字滤波技术的MATLAB实现

MATLAB应用实例：无限脉冲响应数字滤波器

---

5.1 绘图基本原理与步骤

5.1.1 绘图基本原理

今年6月初的武汉还处在雨季的时候，白天气温保持在宜人的25度左右，近7月的时候，温度才慢慢往上，一直到武汉最热的7月份。这一温度变化的过程给我们的感受是连续的、慢慢的变化，但是这样在自然界中连续的变化，目前世界上无论怎样高级的设备，都不能完全体现出最精确的连续变化的温度。你会发现在比设备更高精确度下的数据总是无法表现。

对于电子信息专业的同学，举一个在专业中更常见的例子。学过模电数电的同学就知道，模拟信号信号波形模拟随着信息的变化而变化，其特点是幅度连续；数字信号常用于网络和通信，是自变量、因变量离散的信号。而理想的“连续”的特点是在某一个有限取值范围内能取无限多数值。这样以来，模拟量通常就表示自然界中的量（因为自然界中很多的数值变化都是理论上连续的），数字量通常在机器中表示（因为机器总是存在一定的精度）。如果我们想要对模拟量进行表达，就需要对其进行“采样”，将其转化为数字量。在生活中你见到的显示温度、湿度的电子显示器里就有这样的模数转换。下图就是一个简单的转换电路。

因此我们收集到的 原始数据本身就是离散数据。

机器有它的精度，MATLAB也是，在第二章的时候曾讲到MATLAB存在可以表达的最小正整数，这也是不能绘制完全连续图像的原因之一。更主要的原因，是数据有其本身的精确度，其本身是离散的，我们在MATLAB或是其它软件中所有的绘图都是以离散数据进行的绘图。而当 离散数据足够密集，以至于我们根本分辨不出（或是乍一看分辨不出）是否是离散的，或者我们 把离散的点用直线或者平滑的曲线连接，那么就成了连续的绘图。

5.1.2 绘图的基本步骤

绘制一个简单的图形，大多会经历以下步骤：

1. 原始数据的准备：需要在工作区中准备好需要绘图的数据，通常是一组已经计算好、等待绘图的数据向量，和一组给定范围和精度的自变量向量；

2. 选定图像窗口、子图的位置，即规定图像输出的窗口、在子窗口中绘制的位置；

3. 调用绘图函数绘制图形，如果需要连续绘图应调用hold on；

4. 设置坐标轴范围、刻度、坐标网络；

5. 利用对象属性值或者图形窗口工具栏设置线型、标记类型、大小、线宽（这一步也可在某些绘制函数调用时就调整好）；

6. 添加文本描述（图像名称，坐标轴名称，图例注释，文本注释等）；

7. 图像调整，输出打印。

☆ 例5-1：编写程序，绘制函数$y=2sin(x)cos(2x),x\in [0,6\pi ]$图像。运行下面这个例子，感受绘图的基本过程。思考一下，如果数据自变量不以0.01为间隔而是以0.1为间隔，画出来的图像会有什么不同呢？

clc,clear all,close all
%% 准备原始数据
x1 = 0:0.01:6*pi; % 自变量
y1 = 2*sin(x1).*cos(2*x1); % 函数因变量
%% 选定图像窗口
figure(1) % 选中图像窗口1
%% 调用绘图函数绘制图形，在这一步同时设置线型、标记类型、大小、线宽
plot(x1,y1,'r','linewidth',2)
%% 设置坐标轴范围、刻度、坐标网络
axis([0,20,-3,3]) % 设置坐标轴范围
grid on % 开启格栅
%% 添加文本描述
xlabel('自变量x') % 自变量名称
ylabel('2sin(x)cos(2x)') % 因变量名称
title('绘图举例—例5-1') % 图像名称
legend('函数曲线') % 图例注释

分析：自变量取的间隔越大，描绘函数的点就越少，函数图像就越趋于离散，也就 越不准确，甚至有些峰谷值会被削掉。但是相反，如果间隔过密，就会导致占用内存过高、运行效率低等问题，因此自变量选取的精度需要“两头顾”。

---

5.2 绘制二维图形

5.2.1 最基础的绘图函数：plot函数

plot函数创建将因变量Y对应于自变量X（X会自动进行排序）逐点连接的二维线形图。 plot函数是最基础的绘图函数，当自变量X取值较密时，逐点连接起来的图像看起来就是连续的。

plot函数常用的调用方式如下：

① plot(x, y)：以因变量为y、自变量为x，按照横坐标有序排列绘制图像。其中x、y为等长向量；

② plot(y)：（不推荐）以因变量y、自变量为数组1:length(y)绘制图像；

③ plot(z)：z为复数数组，以横轴为实轴，纵轴为虚轴，绘制$(real(z_j),imag(z_j))$为有序集合的图像；

clc,clear all,close all
%%
subplot(131) % 第一张子图
x1 = linspace(0,2*pi,100);
y1 = sin(x1);
plot(x1,y1,'LineWidth',2) 
% LineWidth属性用于调整线宽，这里为了观察方便调整为2。
% 不调整则为默认值，详细的调整方法见5.3.6节
title('第一张子图') % 添加图像标题
grid on % 添加格栅
%%
subplot(132) % 第二张子图
y2 = [43 64 77 89 100 149 128 122 108 83];
plot(y2,'LineWidth',2)
title('第二张子图') % 添加图像标题
grid on % 添加格栅
%%
subplot(133) % 第三张子图
z = [0+1i, 3+4*1i, 6+3*1i, 6-3*1i,3-4*1i, 0-1i];
plot(z,'LineWidth',2)
title('第三张子图') % 添加图像标题
grid on % 添加格栅

④ plot(A)：矩阵A大小为$m\ast n$，以矩阵的每一列数据为因变量，以数组$1:n$为自变量，绘制$n$条曲线，曲线之间以颜色区分。调整曲线的属性，所有的曲线会一起进行调整，如果需要分开调整每一条曲线的属性，请分开绘图并调整属性；

⑤ plot(x, A)：矩阵A大小为$m\ast n$，以矩阵的每一列数据为因变量，以长度为$n$的数组（行向量与列向量均可）x为自变量，绘制$n$条曲线；

⑥ plot(A, B)：矩阵A、B大小均为$m\ast n$，以矩阵A的第$i$列为自变量、矩阵B的第$i$列为因变量$(1⩽i⩽n)$ 绘制$n$条曲线；

⑦ plot(y, x)：以y为自变量、x为因变量绘制曲线，x、y可以是上述任意一种输入方式，相当于横纵坐标交换。

clc,clear all,close all
%% 第一行第一个子图
subplot(221)
A1 = [22 32 41 43 52 47;
    41 33 46 27 19 10;
    47 58 37 18 4 17;
    42 37 45 43 82 6;
    16 41 37 28 91 8;
    14 38 31 36 75 14;
    18 34 17 64 28 48];
plot(A1,'LineWidth',1.4)
grid on
title('第一行第一个子图')
%% 第一行第二个子图
subplot(222)
A2 = [1 2 3 4 5 6;-2 -3 -4 -5 -6 -7;3 4 5 6 7 8;
    -4 -5 -6 -7 -8 -9;5 6 7 8 9 10;-6 -7 -8 -9 -10 -11];
x1 = 1:6; % x1是一个行向量
plot(x1,A2,'LineWidth',1.4)
grid on
title('第一行第二个子图')
%% 第二行第一个子图
subplot(223)
A3 = rand(2,6); % 2行8列的矩阵
B3 = rand(2,6); % 8行3列的矩阵
plot(A3,B3,'LineWidth',1.4)
grid on
title('第二行第一个子图')
%% 第二行第二个子图
subplot(224)
plot(A2,x1,'LineWidth',1.4)
grid on
title('第二行第二个子图')

在命令行窗口随意输入一个plot绘图程序，例如下面的程序：

clc,clear all,close all
h = plot(1:10,1:10)

MATLAB会弹出一个新窗口，名称为Figure 1。我们将这个窗口成为 图像窗口，MATLAB中的 gcf函数即可返回当前的图像窗口及其属性。有多个图像窗口时需要注意，“当前的图像窗口” 的含义并不是 “在最上层的图像窗口”，而是MATLAB选中的图像窗口。gcf函数在5.3.7节讲到。

此外，变量h会输出我们绘出图像的属性。这时变量h是一个 图像句柄，其中存有绘图的相关属性信息。

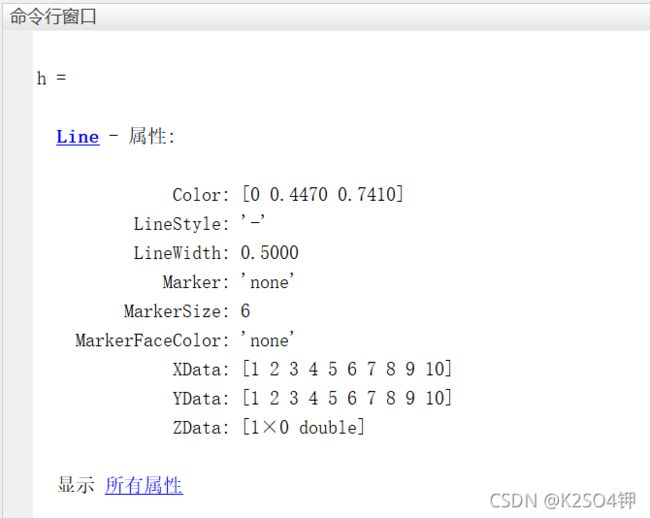
对于plot绘图的属性，我们常调整的是以下属性：‘Color’ （曲线颜色，以颜色对应的符号的字符串或RGB的 $1\ast 3$ 矩阵更改）、‘LineStyle’（线型，以线型符号对应的字符串更改）、 ‘LineWidth’（线宽，以双精度数更改） 、‘Marker’（标记类型，以标记符号对应的字符串更改）、 ‘MarkerSize’（标记大小，以双精度数更改）、‘MarkerFaceColor’（标记填充颜色，以颜色对应的符号的字符串或RGB的 $1\ast 3$ 矩阵更改）、‘MarkerEdgeColor’（标记边缘颜色，以颜色对应的符号的字符串或RGB的 $1\ast 3$ 矩阵更改）。可以 直接在函数中调整，或使用结构体进行调整，或使用set函数进行调整。其全部的属性及含义请参考帮助文档。

这三种调整方法非常重要，对所有的绘图函数属性的调整方法几乎都可以用这三种方法。下面会简单介绍这三种调整方法。具体调整方法、调整所要用到的符号等请参考5.3.6节。

5.2.1.1 函数中直接调整属性

属性可直接在函数中调整。一般写作：plot(x, y, ‘str’, 其它属性调整)。

字符串str用于快速调整曲线的颜色、线型、标记类型。参考5.3.6节，例如 ‘ro’ 就是将曲线颜色调整至红色，标记类型调整为圆形，线型为默认（即实线型）；‘b*–’ 就是将曲线颜色调整为蓝色，标记类型为星号，线型为虚线；‘r’ 就是将曲线颜色调整为红色，标记类型为默认（即不显示标记），线型为默认（即实线型）。

其它属性调整，需要按照属性的含义、对应值的类型来调整。例如，‘LineWidth’ 属性用于调整线宽，后接双精度数；‘MarkerFaceColor’ 用于调整标记填充颜色，以颜色对应的符号的字符串或RGB的 $1\ast 3$ 矩阵调整。

下面给出一个调整示例：

clc,clear all,close all
x = 1:10;
y = rand(1,10);
plot(x,y,'rdiamond-','MarkerSize',10,'MarkerFaceColor','g', ...
    'MarkerEdgeColor','r','LineWidth',2)

5.2.1.2 以结构体的方式调整属性

以结构体的方式调整需要得到绘制图像的图像句柄h。可以将图像句柄h理解为一个结构体，其中存放了图像的属性信息。以结构体的方式对图像进行调整即可。

下面给出一个调整示例：

clc,clear all,close all
x = 0:0.01:2*pi;
y = sin(x);
h = plot(x,y);
h.LineStyle = '-';
h.Color = 'b';
h.Marker = 'none';
h.LineWidth = 2.6;

5.2.1.3 以set函数的方式调整属性

以set函数的方式调整属性同样需要得到绘制图像的图像句柄h。set函数的调用方式为：set(h, 属性调整)。

下面给出一个调整示例：

clc,clear all,close all
x = -2*pi:0.01:2*pi;
y = sin(2*x)./x;
h = plot(x,y);
set(h,'LineWidth',2.4,'Color',[0.2 0.8 0.2],'Marker','none')

再次说明，上面介绍的三种调整属性的方式非常重要，对于大部分的MATLAB绘图函数都适用。学会查看绘图的相关属性、了解常见的属性、灵活使用这三种调整属性的方法，会使你的绘图比别人更高档！

5.2.2 函数绘制：fplot函数

fplot函数用于精确绘制函数或表达式。 常用于绘制参数方程或隐函数。 常用调用方式如下：

fplot(fun)：以函数$y=fun(x)$的形式绘制函数。 fun必须是一个函数句柄（早期MATLAB版本支持字符串输入），且输入必须为一个或多个包含单个变量的函数。默认x的取值为[-5, 5]；

fplot(fun, [xmin, xmax])：限制横坐标范围为[xmin, xmax]；

fplot(funx, funy, [tmin, tmax])：以t范围为[tmin, tmax]来描述函数的横纵坐标：$x=funx(t)$和$y=funy(t)$，再以x和y进行绘图。 此方法可以对隐函数进行绘制。

clc,clear all,close all
h = fplot(@(x) sin(x)+cos(x));
set(h,'Color','r','LineWidth',3)
h
% h1 = fplot(@(x,y) x.^2+y.^2);
% 第5行会报错，因为不是输入的一个或多个包含单个变量的函数。

上面这个例子能看出，fplot函数中的属性常调整的有：‘Color’ （曲线颜色，以颜色对应的符号的字符串或RGB的 $1\ast 3$ 矩阵更改）、‘LineStyle’（线型，以线型符号对应的字符串更改）、 ‘LineWidth’（线宽，以双精度数更改）。可以直接在函数中调整，或使用结构体进行调整，或使用set函数进行调整。具体调整方法请参考5.3.6节。

☆ 例5-2：绘制函数$\{\begin{array}{c}x=sin(t)+cos(t)\\ y=sin(2t)\end{array},t\in [0,4\pi ]$。

clc,clear all,close all
h = fplot(@(t) sin(t)+cos(t), @(t) sin(2*t), [0,4*pi]);
set(h,'Color','r','LineWidth',3)

实际绘制数据时，函数随自变量的变化趋势是未知的，有时候对数据自变量的离散间隔不合理，就会导致函数的变化趋势无法展现。fplot函数相较于plot函数能很好解决这个问题，在函数值变化剧烈的时候自变量离散间隔取小，在函数值变化缓慢的时候自变量离散间隔取大。 因此fplot函数的绘图相较于ezplot和plot函数更清晰准确。

就像下面这个例子：

☆ 例5-3：请分别用ezplot和fplot函数绘制表达式：$y=\frac{2}{3}{e}^{-\frac{t}{2}}cos(\frac{2}{3}t)sin(\frac{1}{t}),t\in [-2\pi ,4\pi ]$，比较二者的区别。

clc,clear all,close all
subplot(121)
h1 = ezplot('(2/3)*exp(-t/2).*cos(2/3*t).*sin(1./t)',[-2*pi,4*pi]);
set(h1,'Color','b','LineWidth',1)
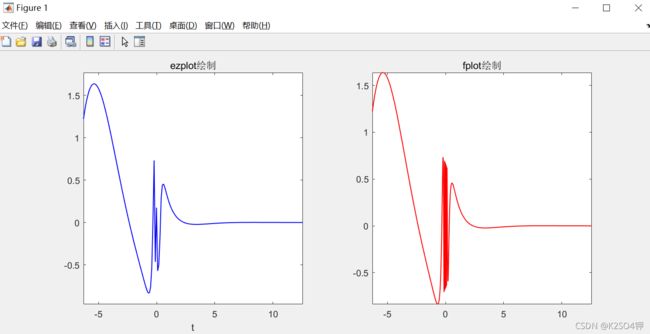
title('ezplot绘制')
subplot(122)
h2 = fplot(@(t)(2/3)*exp(-t/2).*cos(2/3*t).*sin(1./t),[-2*pi,4*pi]);
set(h2,'Color','r','LineWidth',1)
title('fplot绘制')

分析：$sin(\frac{1}{x})$函数会在$x=0$附近强烈振荡。把图像放大来观察，很明显能发现在0附近，fplot函数的绘制结果比ezplot的绘制结果更加精确。

5.2.3 简单函数绘制：ezplot函数

ezplot函数用于简易绘制某一自变量区域内的函数图形。它相较于fplot精度较差，因此如果需要精确绘图则不推荐使用。ezplot函数常用于绘制参数方程或隐函数。

常用调用方式如下：

ezplot(fun)：绘制函数fun所表示的图像。fun可以是字符串，也可以是函数句柄，函数fun(x)是x的显式函数。如果需要绘制二维隐函数，fun则只能使用字符串；

ezplot(fun, [xmin, xmax])：限定绘图的x轴范围；

ezplot(fun, [xmin, xmax, ymin, ymax])：对于 隐函数 作图，限定绘图的x、y范围。

下面为显函数绘图的一个例子：

☆ 例5-4：绘制函数$y=sin(x)+cos(x)$。

clc,clear all,close all
figure
h = ezplot(@(x) sin(x)+cos(x));
set(h,'Color','r','LineWidth',3)
h

其图像句柄的属性中，我们常调整以下几个属性：‘Color’ （曲线颜色，以颜色对应的符号的字符串或RGB的 $1\ast 3$ 矩阵更改）、‘LineStyle’（线型，以线型符号对应的字符串更改）、 ‘LineWidth’（线宽，以双精度数更改） 、‘Marker’（标记类型，以标记符号对应的字符串更改）、 ‘MarkerSize’（标记大小，以双精度数更改）、‘MarkerFaceColor’（标记填充颜色，以颜色对应的符号的字符串或RGB的 $1\ast 3$ 矩阵更改）。可以直接在函数中调整，或使用结构体进行调整，或使用set函数进行调整。具体调整方法请参考5.3.6节。

下面为隐函数绘图的一个例子：

☆ 例5-5：绘制函数$\sqrt{1.5x^2+y^2}=2(1-\frac{y}{\sqrt{1.5x^2+y^2}})$。

clc,clear all,close all
figure
h = ezplot('sqrt(1.5*x.^2+y.^2) = 2*(1-y./(sqrt(1.5*x.^2+y.^2)))');
set(h,'LineColor','r','LineWidth',3)
h

为什么要把显函数和隐函数绘图分开举例呢，细心的同学可能已经发现了，它们的 属性名称有一定的区别。这一点在绘图时尤其要注意，使用某绘图函数时最好先使用该绘图函数简单画一个图形，看一看它的属性名称、各属性的含义。

以隐函数的方式绘图时，我们常调整以下几个属性：‘LineColor’ （曲线颜色，以颜色对应的符号的字符串或RGB的 $1\ast 3$ 矩阵更改）、‘LineStyle’（线型，以线型符号对应的字符串更改）、 ‘LineWidth’（线宽，以双精度数更改） 、‘Fill’（填充颜色，以字符串’on’ 'off’进行更改）。可以直接在函数中调整，或使用结构体进行调整，或使用set函数进行调整。具体调整方法请参考5.3.6节。

————↓———— 提 示 ————↓————

使用函数句柄进行绘图时，一定要使用 (.*) (./) (.^) 使函数向量化，否则会出现警告或报错；使用字符数组（字符串）进行绘图时，MATLAB会自动将字符串中没有经过向量化的函数向量化，虽然此时无需使用 (./) 等操作向量化函数，但是仍建议使用。（主要是因为MATLAB以后的版本中有可能会废除使用字符串作为参数进行绘图）

ezplot不可绘制单变量的隐函数。

————↑———————————↑————

5.2.4 散点图：scatter函数

scatter函数用于绘制二维散点图。 常用调用方式如下：

scatter(x, y)：在向量x和y指定的位置创建一个以空心蓝色圆形（默认）为标记的散点图。该类型的图形也称为气泡图；

scatter(x, y, sz, color)：指定标记的大小和颜色。如果需要绘制大小相等的圆圈，则将sz指定为标量；如果需要绘制大小不等的圆，则将sz指定为长度等于x和y的长度的向量。如果需要以相同的颜色绘制所有圆圈，则将color指定为颜色符号的字符串或RGB的$1\ast 3$矩阵；如果需要使用不同的颜色，则将color指定为向量或RGB的$n\ast 3$矩阵，其中n为数据向量的长度。需要注意，以此种方法更改标记颜色时需先指定标记大小再调整颜色，即必须严格按照调用方式来书写，否则会报错；

scatter(___, mkr)：指定标记类型，下划线表示可以以前述的任意一种方式添加参数；

scatter(___, ‘filled’) ：填充标记。

clc,clear all,close all
x = rand(1,10);
y = rand(1,10);
h = scatter(x,y)

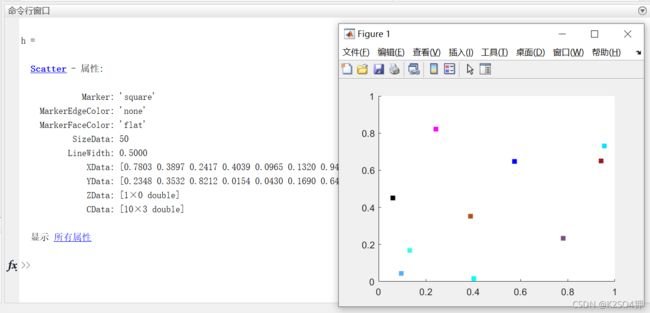
clc,clear all,close all
x = rand(1,10);
y = rand(1,10);
h = scatter(x,y,50,[0.5 0.3 0.5;0.7 0.3 0.1;1,0,1; ...
    0,1,1;0.3,0.7,1;0.2,1,0.9;0.6,0.1,0.1;0,0.9,1;0,0,1;0,0,0;], ...
    'square','filled')

观察scatter函数的属性。我们常更改的属性有：Marker（标记类型，以标记对应符号的字符串更改）、MarkerEdgeColor（标记边缘颜色，以颜色对应的符号的字符串或RGB的 $1\ast 3$ 矩阵更改）、MarkerFaceColor（标记填充颜色，以颜色对应的符号的字符串或RGB的 $1\ast 3$ 矩阵更改）、SizeData（标记大小，以双精度数值更改）、LineWidth（标记线宽，以双精度数值更改）。

这些属性可以直接在函数调用中更改，也可以使用结构体的方式更改，也可以用set函数进行更改。详细的颜色、线型、标记类型请参考5.3.6节。

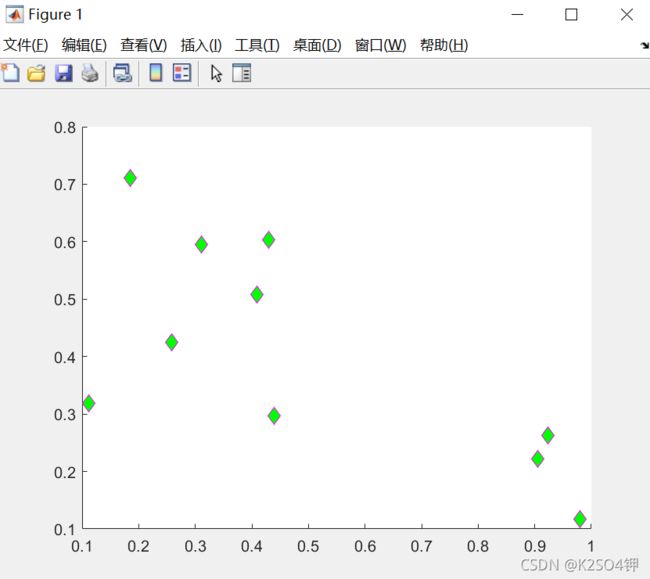
clc,clear all,close all
x = rand(1,10);
y = rand(1,10);
h = scatter(x,y);
set(h,'Marker','diamond','MarkerEdgeColor','m', ...
    'MarkerFaceColor','g','SizeData',65)

5.2.5 绘制线段：line函数

line函数使用向量x和y中的数据在当前坐标区中绘制基本线条。如果x和y中有一个是矩阵或两者都是矩阵，则line将绘制多个线条。

line函数与plot函数的区别在于，line函数可以直接在当前图像窗口进行绘图，而不会像plot函数一样会覆盖原有的图像窗口、重置坐标轴。因此使用line绘图时无需使用hold函数。

其常见的调用方式如下：

line(x, y)：二维图像中绘制基本线条；
line(x, y, z)：三维图像中绘制基本线条。

clc,clear all,close all
x = 0:0.1:2*pi;
y = sin(x);
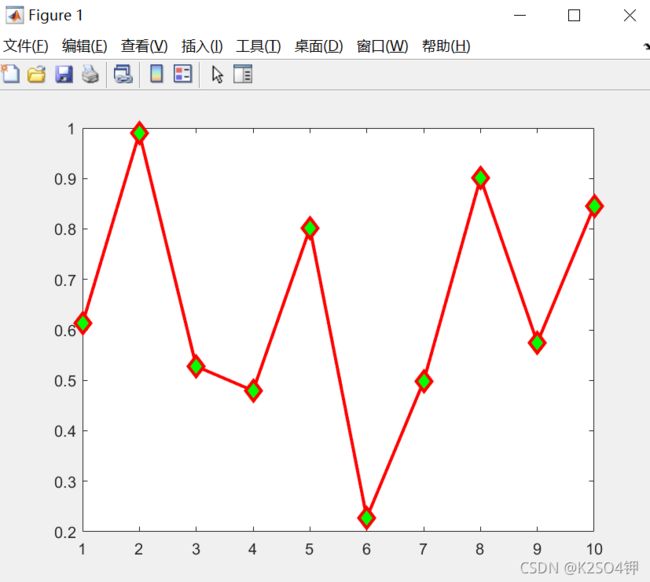
h = line(x,y,'LineWidth',2,'Color','r')

上面这张图是用直线绘制的$sin$函数，这其实就显示出，即使绘制点是由直线连接，当取点密集时，我们还是能看出连续的图像。

line函数常更改的属性有：Marker（标记类型，以标记对应符号的字符串更改）、Color（线条颜色）、MarkerFaceColor（标记填充颜色，以颜色对应的符号的字符串或RGB的 $1\ast 3$ 矩阵更改）、MarkerSize（标记大小，以双精度数值更改）、LineWidth（标记线宽，以双精度数值更改）、LineStyle（线型，以线型符号对应的字符串更改）。

这些属性可以直接在函数调用中更改，也可以使用结构体的方式更改，也可以用set函数进行更改。详细的颜色、线型、标记类型请参考5.3.6节。

clc,clear all,close all
figure
h = line([40,0,20,40,60],[0,40,60,50,60]);
h1 = line([60,80,40],[60,40,0]);
set(h,'LineWidth',5,'Color','r')
set(h1,'LineWidth',5,'Color','r')
set(gca,'Color',[.2,.3,.7]) % 调整坐标轴底色

5.2.6 常用特殊二维图形

常用的绘图函数如下列表：

下面将具体介绍一些常用的二维绘图函数。

5.2.6.1 条形图：bar函数

bar函数用于绘制二维垂直条形图，条形图的高度取决于亟待显示的向量或矩阵。

常用的两种调用方式：

bar(y,‘color’)：以向量y为纵坐标数据，为每一个y的元素绘制条形图，横坐标由1开始递增，'color’为可选项，用于设置条形图颜色；
bar(x,‘color’)：以向量y为纵坐标数据，以向量x为横坐标数据，为每一个y的元素绘制条形图。向量x、y需等长，且向量x应单调递增。

clc,clear all,close all
bar(1:10,randi([0,10],1,10))
% 纵坐标为0-10的随机整数

bar函数也可以输入数组：

bar(A)：以矩阵A的一行数据作为一组绘制条形图，自变量从1递增；
bar(x,A)：以矩阵A的一行数据作为一组绘制条形图，自变量为x，长度应与矩阵A行数相同且单调递增。

这类条形图有2种表现形式，分为累计型和分组型：

bar(x,A,‘stacked’)：累计型；
bar(x,A,‘grouped’)：分组型。

clc,clear all,close all
bar(1:2:5,rand(3,5),'stacked')
legend('1','2','3','4','5') % 设置图例
% 累计型
bar(rand(5,3),'grouped')
legend('数据1','数据2','数据3') % 设置图例
% 分组型

5.2.6.2 直方图：histogram函数

histogram函数的前身是hist函数。hist函数和histc函数用于早期MATLAB版本中绘制直方图、计数bin值，现今版本中仍可使用，但是会被提示“不建议使用”。histogram、histcounts和discretize函数提高了MATLAB中创建和计算直方图的能力，同时也让用户能快速更改直方图的各项属性。

更多关于histogram函数和hist函数的区别，请参考这篇CSDN博客：matlab中hist和histogram的区别，也可以在MATLAB帮助文档中查找。这里不多做介绍。

histogram函数是一个非常实用的统计函数，功能十分强大，但同时使用起来也相对复杂。这里只介绍该函数的基础应用。

histogram函数用于绘制一组数据的直方图，常用于统计一个向量中的各个数据落在某一数值范围的数量，创建的直方图是属于数值数据的条形图类型。常用的调用方式为：

histogram(X,nbins)：输入参数为一个数组X和一个正整数标量nbins。nbins规定了分组的数量，如果不输入参数nbins，MATLAB会自动按照整数进行分组。
histogram(X,edges)：输入参数edges为一个向量，规定了统计的各个边界，将数据X划分到每一组边界之中，每个bin包含其左边界而不包含右边界。

clc,clear all,close all
histogram(randi([1,200],1,100)/10)
% 产生0.1-20的随机数矩阵
histogram(randi([1,200],1,100)/10,40)
% 规定分组数量40
histogram(randi([1,200],1,100)/10,[0,10,15,16,17,18,19,20])
% 规定边界，规定分组数量20

h1 = histogram(X,nbins)可将histogram的属性赋给变量h1，h1即为一大小为$1\ast 1$的histogram变量。同时命令行窗口输入h1并按下回车即可查看histogram变量h1中的属性。

clc,clear all,close all
clc,clear all,close all
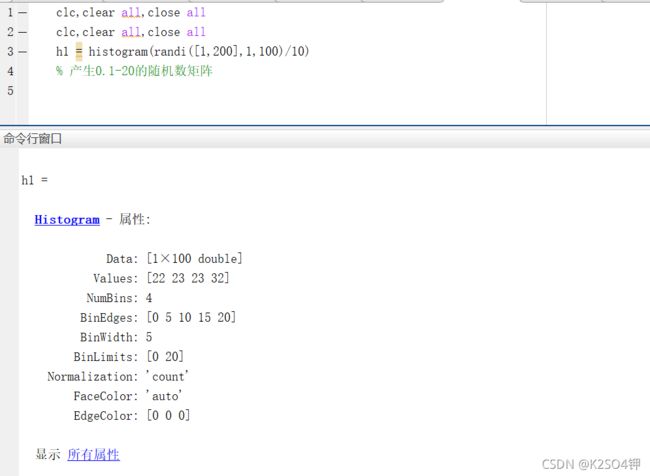
h1 = histogram(randi([1,200],1,100)/10)
% 产生0.1-20的随机数矩阵

histogram变量可以类似于结构体的方式更改属性，这便于用户快速调整绘图结果。

如下图所示，笔者使用上文中的代码绘出图像后，在命令行窗口键入了代码下面的代码段并回车。

h1.NumBins = 10

随即观察到histogram变量h1中的分组数量的属性发生变化，并且之前绘出的图像也随之发生变化。

常调整的属性有两个。一个是NumBins，用于调整分组的数量；另一个是BinEdges，用于调整每个分组的边缘（最大值和最小值）。

同理，histogram变量中的其它属性也可以进行相应调整，方法仍然是类似于结构体的使用方法。这极大方便用户在使用该函数时能根据需要实时对直方图进行直观调整。

5.2.6.3 饼状图：pie函数

饼状图（或饼图）可以使统计结果直观化。MATLAB中提供了两种绘制饼状图的函数：

pie(X)：使用数组X中的数据绘制二维饼图。饼图的每个扇区代表X中的一个元素；
pie3(X)：使用数组X中的数据绘制三维饼图。饼图的每个扇区代表X中的一个元素。

pie与pie3函数在调用方式上几乎相同，区别只在展示方式是二维还是三维上。

clc,clear all,close all
X = [4 5 3 10 7 4 8 1];
pie(X)
pie3(X)

饼状图上的标注可以加以修改，方法是在pie函数中加入含有字符串的元胞数组，元胞中的每一个元素会依次放在饼状图对应位置旁边。

clc,clear all,close all
X = [4 5 3 10 7 4 8];
label = {'第1组','第2组','第3组', ...
    '第4组','第5组','第6组','第7组',};
pie(X,label)

如果你还想让其中某一块突出，还需要在pie函数中增加一个数组（行向量）。这个数组长度应与输入数组X的长度相同，且其每个元素的值为0或1。“0”表示对应的X元素不突出，“1”表示对应的X元素突出。

clc,clear all,close all
X = [4 5 3 10 7 4 8];
label = {'第1组','第2组','第3组', ...
    '第4组','第5组','第6组','第7组'};
explode = [0 0 1 0 1 0 1];
pie(X,explode,label)

当然你会发现，如果采用设置label的方式自定义标签，那么饼状图每一份的比例就不会展示。如果既需要展示比例，又需要自定义标签，可以使用legend函数（此时pie3函数的排版会比pie函数的排版稍微好看点）。如果需要为图像命名，可以使用title函数。这两个函数在5.3.5节中会详细讲述。

clc,clear all,close all
X = [4 5 3 10 7 4 8];
explode = [0 0 1 0 1 0 1];
pie3(X,explode)
legend('第1组','第2组','第3组','第4组','第5组','第6组','第7组');
title('每组占比')

5.2.6.4 误差带图：errorbar函数

errorbar函数会以x为自变量y为因变量绘制数据线图，并在每个数据点处绘制误差条。误差条err需要用户自行设定，调用时输入参数x、y、err都应为等长的数组。常用的调用方式如下：

errorbar(x,y,err)：以x为自变量y为因变量绘制数据线图，以err在每个数据点处绘制垂直误差条（见下图左上角）；
errorbar(x,y,err,‘horizontal’)：以x为自变量y为因变量绘制数据线图，以err在每个数据点处绘制水平误差条（见下图右上角）；
errorbar(x,y,err,‘both’)：以x为自变量y为因变量绘制数据线图，以err在每个数据点处绘制水平、垂直的误差条（水平和垂直的误差相同，见下图左下角）；
errorbar(x,y,err,‘o’)：仅以err在每个数据点处绘制垂直误差条（见下图右下角）；

需要注意的是，上面的调用方式中用户输入的误差长度err是指数据点上方和下方的误差长度（并不是二者之和）。因此对于每个数据点，误差条的长度是用户设置err的2倍。

clc,clear all,close all

subplot(2,2,1) % 绘图结果左上角的图像
x = 1:10:100;
y = [10 40 60 100 70 65 40 15 35 60];
err = [5 10 10 5 15 10 5 5 10 10];
errorbar(x,y,err)

subplot(2,2,2) % 绘图结果右上角的图像
x = 1:10:100;
y = [10 40 60 100 70 65 40 15 35 60];
err = [5 10 10 5 15 10 5 5 10 10];
errorbar(x,y,err)
errorbar(x,y,err,'horizontal')

subplot(2,2,3) % 绘图结果左下角的图像
x = 1:10:100;
y = [10 40 60 100 70 65 40 15 35 60];
err = [5 10 10 5 15 10 5 5 10 10];
errorbar(x,y,err)
errorbar(x,y,err,'both')

subplot(2,2,4) % 绘图结果右下角的图像
x = 1:10:100;
y = [10 40 60 100 70 65 40 15 35 60];
err = [5 10 10 5 15 10 5 5 10 10];
errorbar(x,y,err)
errorbar(x,y,err,'both','o')

如果误差条在正方向和负方向长度不同，可以以下面的方式调用：

errorbar(x, y, yneg, ypos, xneg, xpos)

其中yneg和ypos分别指垂直误差条负方向、正方向的长度，xneg和xpos分别指水平误差条负方向、正方向的长度，其均为与x、y长度相同的数组。调用时注意输入参数的顺序。

clc,clear all,close all

subplot(1,2,1) % 绘图结果左侧的图像
x = 1:10:100;
y = [10 40 60 100 70 65 40 15 35 60];
yneg = [3 2 4 3 1 3 4 2 1 1];
ypos = [3 2 2 1 2 2 1 4 5 5];
errorbar(x,y,yneg,ypos)

subplot(1,2,2) % 绘图结果右侧的图像
x = 1:10:100;
y = [10 40 60 100 70 65 40 15 35 60];
yneg = [3 2 4 2 2 3 4 2 1 1];
ypos = [2 1 2 1 2 4 1 2 2 5];
xneg = [1 2 4 3 1 3 4 1 1 3];
xpos = [3 2 2 5 3 2 1 4 3 4];
errorbar(x,y,yneg,ypos,xneg,xpos)

其它调整参数请参考帮助文档。

5.2.6.5 箱线图：boxplot函数

boxplot函数用于绘制给定数据的箱线图。若输入参数为一个数组，则绘制该数组对应数据的箱线图；若输入参数为一个矩阵，则按照矩阵每一列绘制对应数据的箱线图。箱线图可以表现出一组数据的中位数、最大最小值、第一个和第三个四分位点、离群值，是统计中相当重要的一个MATLAB函数。

boxplot函数常见调用方式如下：

boxplot(x)：输入参数x为一个数组，绘制该数组对应数据的箱线图；
boxplot(A)：输入参数A为一个矩阵，按照矩阵每一列绘制对应数据的箱线图；

clc,clear all,close all
A = normrnd(5,1,100,20);
% 创建一个平均值为5、标准差为1的100*20正态分布随机数矩阵
h = boxplot(A);

如上图，以一个100*20的正态分布随机数矩阵为输入参数，调用boxplot函数后，会以列为数据绘制箱线图。对于每一个箱线图，上方或下方红色的“+”号代表数据的离群值；蓝色“盒子”两段虚线代表最大值和最小值；蓝色“盒子”上端代表第三个四分位点，下端代表第一个四分位点；蓝色“盒子”中间的红线代表数据的中位数。 在图中点击对应的点会显示该点的一些信息。

调用boxplot时可以更改一些属性，以便输出更美观、更符合要求的箱线图。通常以如下方式调用函数：

boxplot(A, ‘name1’, value1, ‘name2’, value2, …)，具体的name和value如何取值见下表。

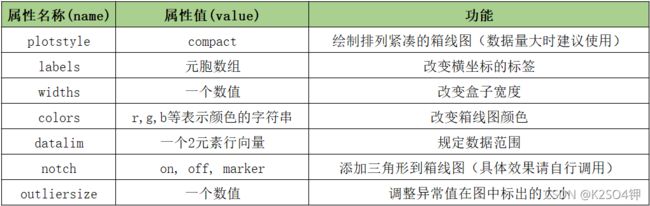
需要注意，属性值value在输入为英文单词时要使用字符串（即两侧加单引号，例如compact就要输入’compact’，而如果需要输入一个数值则不需，几乎所有函数的调用都是这样）。更多的属性调整参考帮助文档。

clc,clear all,close all
A = normrnd(5,1,100,5);
% 创建一个平均值为5、标准差为1的100*20正态分布随机数矩阵
h = boxplot(A,'plotstyle','compact','labels',{ ...
    '第1组','第2组','第3组','第4组','第5组'},'notch','on');

5.2.6.6 火柴杆状图：stem函数

stem函数以自变量为x、因变量为y绘制火柴杆图（也称茎秆图），常用于 绘制离散函数，在信号与系统、数字信号处理中使用频繁。常用调用方式如下：

stem(x,y)：以自变量为x、因变量为y绘制火柴杆图，x、y为等长数组；
stem(x,y,‘filled’)：以自变量为x、因变量为y绘制实心点火柴杆图，x、y为等长数组。

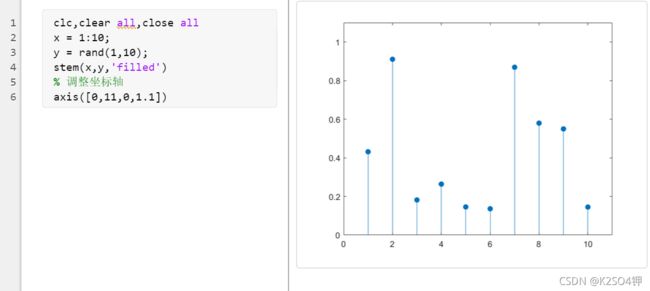
clc,clear all,close all
x = 1:10;
y = rand(1,10);
stem(x,y,'filled')
% 调整坐标轴
axis([0,11,0,1.1])

5.2.6.7 向量场：quiver函数

quiver函数可用于绘制二维向量与向量场。对于向量$F=a{e}_x+b{e}_y$，quiver函数需给定该向量的起点和方向。quiver函数常用调用方式为：

quiver(x,y,u,v)：x、y、u、v可以是标量，也可以是等长的数组。x、y表示向量起点的横纵坐标，u、v规定向量的方向；
quiver(x,y,u,v,scale)：scale规定向量的长度，其值为1则等值显示矢量的长度，值为其它时则显示对应倍数的矢量长度；
quiver(x,y,u,v,LinSpec)：用于规定向量的属性，比如颜色，线型等，详细内容请查看帮助文档。

所绘制的向量的方向是$arctan(\frac{v}{u})$，长度是$\sqrt{u^2+v^2}$。

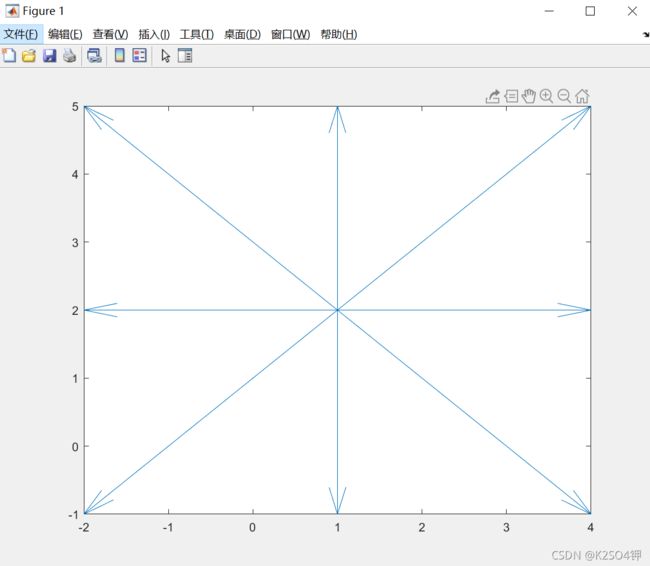
clc,clear all,close all
x = [1 1 1 1 1 1 1 1];
y = [2 2 2 2 2 2 2 2];
u = [0 1 1  1  0 -1 -1 -1];
v = [1 1 0 -1 -1 -1  0  1];
quiver(x,y,u,v,3)

---

思考题5

☆ 思考题5-1：分别使用plot、fplot、ezplot函数绘制$y=\frac{2}{3}{e}^{-\frac{t}{2}}cos(\frac{2}{3}t)$，其中$t\in [0,4\pi ]$。

☆ 思考题5-2：仔细回忆已学的绘图内容。你能想到多少种方法绘制一个单位圆？

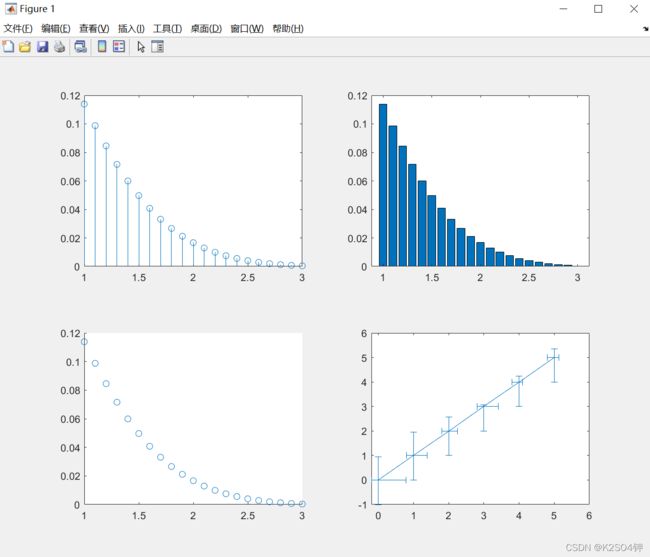
☆ 思考题5-3：在“#”符号之间的空白处补全代码。将一个图形窗口分割成4个子图窗口。前三个图像窗口分别来显示函数 $y=e^{-2x}sin(x)$ $,x=1:0.1:3$ 的离散数据火柴杆图、条形图、散点图，对于第四个图像窗口，绘制函数 $y=e^{2x}sin(x)$ $,x=0:1:5$ 的误差带图，使用rand函数为该函数6个点每一个点的x轴正方向和y轴的正方向设置误差，x轴负方向和y轴负方向的误差设置为固定值0.2和1。

clc,clear all,close all
subplot(221) % 分割图像窗口
####################

####################

subplot(222)
####################

####################

subplot(223)
####################

####################

subplot(224)
####################

####################

☆ 思考题5-4：现有一$20\ast 20$的数据矩阵如下：

data = [83,49,48,61,53,50,89,98,2,67,20,82,41,64,47,19,78,55,53,69;
    2,44,24,72,24,78,3,65,99,54,43,27,82,96,43,29,36,73,54,71;
    5,45,85,23,49,72,49,81,17,70,49,60,72,25,47,10,67,53,87,45;
    17,31,20,12,63,91,17,46,11,67,13,3,97,68,78,58,42,100,49,2;
    65,51,23,30,68,90,98,44,38,18,59,43,54,29,33,69,85,22,40,34;
    74,52,18,32,40,34,72,83,20,13,23,32,33,68,79,55,84,11,68,43;
    65,82,23,43,37,70,51,9,49,100,39,17,11,70,48,43,26,11,75,28;
    46,80,44,51,99,20,48,14,34,18,59,18,62,7,4,65,62,7,53,20;
    55,65,32,9,4,4,6,18,96,4,26,43,78,26,18,65,59,41,35,83;
    30,38,93,27,89,75,69,40,93,57,30,10,43,23,73,68,55,45,15,43;
    75,82,44,81,92,51,5,84,6,89,62,60,10,67,48,64,87,37,59,89;
    19,54,19,3,80,48,8,81,74,67,27,48,27,85,16,95,27,77,27,40;
    69,36,91,93,10,91,53,7,27,20,83,70,16,35,35,21,32,63,5,77;
    19,94,98,74,27,61,10,40,43,37,99,70,29,79,61,71,12,78,76,40;
    37,88,44,49,34,62,82,53,55,47,74,64,45,68,20,24,94,94,25,81;
    63,56,12,58,68,86,82,42,95,99,35,4,53,1,74,12,65,98,45,76;
    79,63,26,24,14,81,73,66,42,16,59,7,46,61,25,61,48,20,69,38;
    9,59,41,46,73,58,15,63,99,86,11,32,88,39,92,46,64,14,36,22;
    93,21,60,97,11,19,66,30,31,65,91,54,52,92,27,46,55,70,74,80;
    78,31,27,55,66,24,52,44,71,38,88,66,95,1,77,67,65,10,40,95];

该矩阵每一列代表一个组。按要求完成以下题目。

（1）使用histogram函数，统计1-10组所有数据，值分布在1-40、41-80、81-100的个数，绘制直方图；统计该矩阵所有数据，值分布在1-20、21-40、41-80、81-100的个数，绘制直方图。

（2）对于每一组数据，绘制其箱线图，并具体说明图像的含义；对于所有数据，绘制箱线图。

☆ 思考题5-5：按要求绘制下面的图形：

（1）绘制参数方程$\{\begin{array}{c}x=t^{2}sin(4t)\\ y=cos(4t)\end{array}$，其中$t\in [0,2\pi ]$。

（2）绘制隐函数$x^2+(y-\sqrt{|x|}{)}^2=1$，其中$x\in [-1,1]$，$y\in [-1,1.6]$。

---

部分思考题答案

思考题5-1

clc,clear all,close all
x = linspace(0,4*pi,1001);
y = (2/3)*exp(-x/2).*cos(2*x/3);
subplot(1,3,1) % 第一个子图放置plot的绘制结果
plot(x,y)
subplot(1,3,2) % 第二个子图放置fplot的绘制结果
fplot(@(x)(2/3)*exp(-x/2).*cos(2*x/3),[0,4*pi])
subplot(133) % 第三个子图放置ezplot的绘制结果
ezplot('(2/3)*exp(-x/2)*cos(2*x/3)',[0,4*pi])

思考题5-2

clc,clear all,close all

subplot(221) % 第一种方法：分为四个方程，用plot绘制
x=linspace(0,1,101);
plot(x,sqrt(1-x.*x))
hold on
plot(x,-sqrt(1-x.*x))
hold on
x=linspace(-1,0,101);
plot(x,sqrt(1-x.*x))
hold on
plot(x,-sqrt(1-x.*x))

subplot(222) % 第二种方法：写出参数方程，用plot绘制
t=linspace(0,2*pi,1001);
x=cos(t);
y=sin(t);
plot(x,y)

subplot(223) % 第三种方法：用fplot分别绘制上半圆和下半圆
fplot(@(x)sqrt(1-x.*x))
hold on
fplot(@(x)-sqrt(1-x.*x))

subplot(224) % 第四种方法：ezplot绘制隐函数
ezplot('x^2+y^2=1')

% 其它方法略

思考题5-3

clc,clear all,close all
subplot(221)
####################
x = 1:0.1:3;
y = exp(-2*x).*sin(x);
stem(x,y)
####################

subplot(222)
####################
bar(x,y)
####################

subplot(223)
####################
scatter(x,y)
####################

subplot(224)
####################
x1 = 0:1:5;
y1 = x1;
xp = rand(1,length(x1));
xn = zeros(1,length(x1))+0.2;
yp = rand(1,length(x1));
yn = zeros(1,length(x1))+1;
errorbar(x1,y1,yn,yp,xn,xp)
####################

思考题5-4

clc,clear all,close all
data = [83,49,48,61,53,50,89,98,2,67,20,82,41,64,47,19,78,55,53,69;
    2,44,24,72,24,78,3,65,99,54,43,27,82,96,43,29,36,73,54,71;
    5,45,85,23,49,72,49,81,17,70,49,60,72,25,47,10,67,53,87,45;
    17,31,20,12,63,91,17,46,11,67,13,3,97,68,78,58,42,100,49,2;
    65,51,23,30,68,90,98,44,38,18,59,43,54,29,33,69,85,22,40,34;
    74,52,18,32,40,34,72,83,20,13,23,32,33,68,79,55,84,11,68,43;
    65,82,23,43,37,70,51,9,49,100,39,17,11,70,48,43,26,11,75,28;
    46,80,44,51,99,20,48,14,34,18,59,18,62,7,4,65,62,7,53,20;
    55,65,32,9,4,4,6,18,96,4,26,43,78,26,18,65,59,41,35,83;
    30,38,93,27,89,75,69,40,93,57,30,10,43,23,73,68,55,45,15,43;
    75,82,44,81,92,51,5,84,6,89,62,60,10,67,48,64,87,37,59,89;
    19,54,19,3,80,48,8,81,74,67,27,48,27,85,16,95,27,77,27,40;
    69,36,91,93,10,91,53,7,27,20,83,70,16,35,35,21,32,63,5,77;
    19,94,98,74,27,61,10,40,43,37,99,70,29,79,61,71,12,78,76,40;
    37,88,44,49,34,62,82,53,55,47,74,64,45,68,20,24,94,94,25,81;
    63,56,12,58,68,86,82,42,95,99,35,4,53,1,74,12,65,98,45,76;
    79,63,26,24,14,81,73,66,42,16,59,7,46,61,25,61,48,20,69,38;
    9,59,41,46,73,58,15,63,99,86,11,32,88,39,92,46,64,14,36,22;
    93,21,60,97,11,19,66,30,31,65,91,54,52,92,27,46,55,70,74,80;
    78,31,27,55,66,24,52,44,71,38,88,66,95,1,77,67,65,10,40,95];
    
%% 使用histogram函数，统计1-10组所有数据，值分布在1-40、41-80、81-100的个数，绘制直方图
subplot(221) % 第一行第一列的子图
h = histogram(data(:,1:10));
h.NumBins = 3;
h.BinEdges = [1 40 80 100];

%% 统计该矩阵所有数据，值分布在1-20、21-40、41-80、81-100的个数，绘制直方图
subplot(222) % 第一行第二列的子图
h = histogram(data);
h.NumBins = 4;
h.BinEdges = [1 20 40 80 100];

%% 对于每一组数据，绘制其箱线图，并具体说明图像的含义
subplot(223) % 第二行第一列的子图
boxplot(data)
% 图像含义见5.2.6.5节
% 上方或下方红色的“+”号代表数据的离群值；蓝色“盒子”两段虚线代表最大值和最小值；
% 蓝色“盒子”上端代表第三个四分位点，下端代表第一个四分位点；
% 蓝色“盒子”中间的红线代表数据的中位数

%% 对于所有数据，绘制箱线图
subplot(224)
data1 = reshape(data,numel(data),1); % 将所有数据转化为一列
boxplot(data1)

思考题5-5

clc,clear all,close all
%% 第一问
subplot(121)
t = 0:.01:2*pi;
fplot(@(t) t.^2.*sin(4*t), @(t) cos(4*t))
%% 第二问
subplot(122)
ezplot('x^2+(y-sqrt(abs(x)))^2=1',[-1 1 -1 1.6])

---

撰写：邓云泽、林耀
审核：华中师范大学HelloWorld程序设计协会工作人员

---

1. 刘浩, 韩晶. MATLAB R2018a 完全自学一本通[M]. 北京：电子工业出版社. 2019. ↩︎