BP神经网络原理（详细推导）

---

前言

BP神经网络（Back propagation neural network）全称为多层前馈神经网络，其用于解决非线性问题。整个神经网络的步骤为：输入层接收外界的输入，隐藏层和输出层的神经元对输入的特征或信号通过权重矩阵进行加工，最终输出结果。过程中最重要的是获得加工所要的权重，本质上说神经网络的学习过程就是在学习神经元与神经元之间连接的权重。

---

提示：以下是本篇文章正文内容，下面案例可供参考

第一步：正向传播激活神经网络

A.变量说明

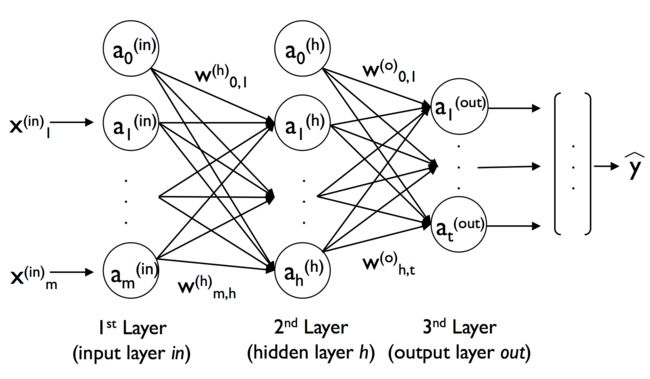
关于BP神经网络的正向传播，我们以上图为例对变量进行一下说明：

• $x_i^{(in)}，a_i^{(in)}$ : 二者均表示输入层的第$i$个输入单元（这样做是为了和后面的进行统一，二者相等的原因是输入层的神经元不起激活作用）；
• $w_{m,h}^{(h)}$ :输入层的第$m$个单元与隐藏层的的第$h$个单元之间的权重（⚠️权重的标识很重要，而且不同的参考书用的也不同，读者一定要弄清楚）
• $z_i^{(h)}$ : 隐藏层的第$i$的净输入单元，$z_i^{(h)}=w_{1,i}^{(h)}{a}_1^{(in)}+...+w_{m,i}^{(h)}{a}_m^{(in)}$；
• $a_i^{(h)}$ : 隐藏层的第$i$的隐藏单元，$a_i^{(h)}=\varphi (z_i^{(h)})$；
• $w_{h,t}^{(o)}$ :隐藏层的第$h$个单元与输出层的的第$t$个单元之间的权重（⚠️权重的标识很重要，而且不同的参考书用的也不同，读者一定要弄清楚）
• $z_i^{(out)}$ : 输出层的第$i$的净输入单元，$z_i^{(out)}=w_{1,i}^{(out)}{a}_1^{(h)}+...+w_{h,i}^{(out)}{a}_h^{(h)}$；
• $a_i^{(out)}$ : 输出层的第$i$的输出单元，$a_i^{(out)}=\varphi (z_i^{(out)})$；
• $y^{[i]},a^{[i]}$: 分别代表一组数据的实际结果中的第$i$个（上角标视为索引），经过神经网络输出的第$i$个；
• 关于激活函数，我们采用 sigmoid 函数 $\varphi (x)=\frac{1}{1+e^{-x}}$ ;

B.正向传播

熟悉完上面的量的意义之后，我们通过线性代数的知识导出BP神经网络的正向传播过程：

首先，输入层的各个单元${\mathbf{A}}^{(in)}$(不妨设阶数为：n*m )和通过指向隐藏层的权重矩阵${\mathbf{W}}^{(h)}$（阶数：m * h）做点乘，得到隐藏层的净输入向量：${\mathbf{Z}}^{(h)}$（阶数： n * h）；

其次，将隐藏层的净输入向量进行激活，得到${\mathbf{A}}^{(h)}$，${\mathbf{A}}^{(h)}=\varphi （{\mathbf{Z}}^{(h)}）$（阶数：n * h）；

再其次：${\mathbf{a}}^{(h)}$通过指向输出层的权重矩阵${\mathbf{W}}^{(out)}$（阶数：h * t），得到输出层的净输入向量：${\mathbf{Z}}^{(out)}$（n * t）；

最后，将输出层的净输入向量进行激活，得到得到${\mathbf{A}}^{(out)}$，${\mathbf{A}}^{(out)}=\varphi （{\mathbf{Z}}^{(out}）$（阶数：n * t），即我们的输出结果。

这其中涉及的矩阵运算罗列如下：

1. ${\mathbf{Z}}^{(h)}={\mathbf{A}}^{(in)}{\mathbf{W}}^{(h)}$;
2. ${\mathbf{Z}}^{(out)}={\mathbf{A}}^{(h)}{\mathbf{W}}^{(out)}$;

BP神经网络的正向传播过程相对比较简单，弄清楚需要对上面变量的标识熟练掌控以及要有线性代数的基础，另外上面的表述并没牵扯到偏置单元，下面我们介绍下偏置单元的内容

C.偏置单元

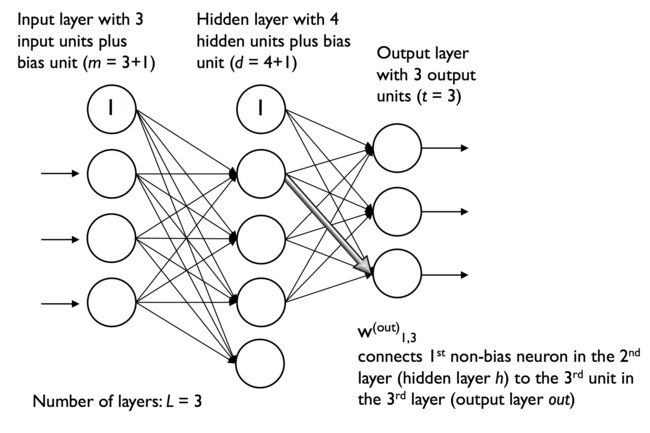
关于偏置单元的设置，通常输入层的激发单元（神经元）组成的是输入单元和偏置单元，隐藏层的激发单元（神经元）组成的是隐藏单元和偏置单元。但是为方便起见，将偏置单元更改为单独的偏置向量，单独的偏置向量的设定和之前的以权重变量作为偏置（也就是偏置单元设定为1）的操作二者相同，只是形式不同。
采用这样形式的优点：

• 代码更加高效并且便于阅读，权重矩阵的维度可完全用层与层之间的神经元个数表示，而无偏置单元的参与；
• 这样的操作也在常用的深度学习库中被采用；

如上图所示：输入层（Input layer）中共有3+1个输入单元，1个为偏置单元。隐藏层（Hidden layer）中共有4 + 1个隐藏单元，1个为偏置单元。采用偏置单元更改为单独的偏置向量的形式，尚若我们有100组数据，一组数据对应3个特征值，那么我们就只需考虑输入层（Input layer）和隐藏层（Hidden layer）之间的权重矩阵为： 一个 3 * 4的权重矩阵 + 一个 1 * 4 的偏置向量；

可能读者有疑问️两个向量个维度不相同，那么计算不会报错吗？不会，因为numpy具有广博机制，一个权重矩阵的列数和第二个单元的行数相同，就会采用广播机制，见下面代码示例。

print(np.array([[1,2],[1,2]]),'\n')
print(np.array([3,2]),'\n')
print(np.array([[1,2],[1,2]])+np.array([3,2]),'\n')
#s输出结果如下，可见计算正常进行
[[1 2]
 [1 2]] 

[3 2] 

[[4 4]
 [4 4]]

第二步：误差逆向传播

1.损失函数

我们通过第一步进行了BP神经网络的正向传播，得到输出结果向量，输出结果向量和实际的向量之间存在差异，如何用数学的形式进行表示？这就需要损失函数的发挥作用。为简单起见，我们首先从1组输入数据（阶数：1 * m）入手再过渡到多组数据（阶数：n * m）的形式，由易到难。

损失函数的一般形式(线性回归形式)：
$$J（\mathbf{W}）=\frac{1}{2}\Vert {\mathbf{a}}^{\mathbf{o}\mathbf{u}\mathbf{t}}-\mathbf{y}{\Vert }_2^2=\frac{1}{2}\sum _{i=1}^m(y^{[i]}-a^{[i]}{)}^2$$

损失函数的一般形式(逻辑回归形式)：
$$J（\mathbf{W}）=\frac{1}{2}\Vert {\mathbf{a}}^{\mathbf{o}\mathbf{u}\mathbf{t}-\mathbf{y}}{\Vert }_2^2=-\sum _{i=1}^m[y^{[i]}log(a^{[i]}+(1-y^{[i]})log(1-a^{[i]})]$$

注： $y^{[i]},z^{[i]}$: 分别代表一组数据的实际结果中的第$i$个（上角标视为索引），经过神经网络输出的第$i$个（上角标视为索引）；

可以看到损失函数是$a^{out}$的函数，而$a^{out}$又是通过已知的输入变量（固定）通过层与层之间的权重矩阵得到，所以损失函数是整个神经网络的权重矩阵的函数。此时我们明确了损失函数的自变量是权重，按照梯度下降的思想，要想损失函数最小化，就要找到损失函数关于各个权重的梯度（偏导数），然后在其相反的方向上进行变化。

2.哈达玛积（Hadamard product）

为了更好的表达误差，我们采用一种运算方式，可以让我们的结果更加简洁：哈达玛积

这种运算方式定义如下：
$$\left[\begin{array}{c}a\\ b\end{array}\right]\odot \left[\begin{array}{c}c\\ d\end{array}\right]=\left[\begin{array}{c}ac\\ bd\end{array}\right]$$
即：
$$\left[\begin{array}{c}1\\ 3\end{array}\right]\odot \left[\begin{array}{c}2\\ 4\end{array}\right]=\left[\begin{array}{c}2\\ 12\end{array}\right]$$

哈达玛乘积如何由numpy实现？

np.array([1,2,3]) * np.array([1,2,3])
#输出结果为：
array([1, 4, 9])
#所以，在numpy中，实现哈达玛乘积只需将两个大小相同的向量直接相乘

3.理解误差逆向传播

上面我们介绍了损失函数和一种运算方式，我们提到想要通过计算损失函数关于权重的梯度也就是偏导数来实现梯度下降，那么我们该如何下手？也就是如何得到以下二式？

$$\frac{\partial J(\mathbf{W})}{\partial w_{m,h}^{(h)}}$$

$$\frac{\partial J(\mathbf{W})}{\partial w_{h,t}^{(out)}}$$

上面我们提到损失函数是$a^{out}$的函数，$a^{out}$是权重变量的函数。通过最开始神经网络的描述，我们直观的感觉这里面层层环绕，一层接着一层，直接获得上面两个式子看来不太容易。我们不妨一层层一层看，离我们损失函数最近（也就是直接影响损失函数）的是$a_i^{out}$，其次是$z_i^{(out)}$（输出层的净输入单元，尚未激活），最后才是权重$w_{h,t}^{(out)}$。考虑到这种关系，我们不妨先求损失函数关于$z_i^{(out)}$偏导数，然后再求解关于其$w_{h,t}^{(out)}$的偏导数。

这里的计算本质上是链式求导法则，计算机代数中自动微分（Automatic Differentiation）可以很好的解决这样的问题，但是我们作为初学者，要用代码一行一行的将其表示出来。

基于上面的分析，我们从输出层考虑：
$${\delta }_i^{out}=\frac{\partial J(\mathbf{W})}{\partial a_i^{(out)}}\frac{\partial a_i^{(out)}}{\partial z_i^{(out)}}$$
这其中${\delta }_i^{out}$称为误差项，而 $a_i^{(out)}=\varphi (z_i^{(out)})$,所以：
$$\frac{\partial a_i^{(out)}}{\partial z_i^{(out)}}={\varphi }^{{}^{\prime }}(z_i^{(out)})$$
即：
$${\delta }_i^{out}=\frac{\partial J(\mathbf{W})}{\partial a_i^{(out)}}{\varphi }^{{}^{\prime }}(z_i^{(out)})$$
利用哈达玛积并且写成向量的形式更加简洁：
$${\mathbf{\delta }}^{out}=\frac{\partial J(\mathbf{W})}{\partial {\mathbf{a}}^{(out)}}\odot {\mathbf{\varphi }}^{{}^{\prime }}({\mathbf{Z}}^{(\mathbf{o}\mathbf{u}\mathbf{t})})$$
又因为我们知道损失函数关于${\mathbf{a}}^{(out)}$的函数表达式，求偏导可得$\frac{\partial J(\mathbf{W})}{\partial {\mathbf{a}}^{(out)}}={\mathbf{a}}^{\mathbf{o}\mathbf{u}\mathbf{t}}-\mathbf{y}$

所以：
$${\mathbf{\delta }}^{out}=（{\mathbf{a}}^{\mathbf{o}\mathbf{u}\mathbf{t}}-\mathbf{y}）\odot {\mathbf{\varphi }}^{{}^{\prime }}({\mathbf{Z}}^{(\mathbf{o}\mathbf{u}\mathbf{t})})$$

至此，我们得到${\mathbf{\delta }}^{out}$也就是损失函数关于${\mathbf{z}}^{(out)}$的偏导数，但是我们最终的目的是其关于权重的偏导数，考虑到${\mathbf{Z}}^{(out)}$ = ${\mathbf{A}}^{\mathbf{h}}{\mathbf{W}}^{\mathbf{o}\mathbf{u}\mathbf{t}}$,所以：

$$\frac{\partial J(\mathbf{W})}{\partial {\mathbf{W}}^{(\mathbf{o}\mathbf{u}\mathbf{t})}}=（{\mathbf{A}}^{\mathbf{h}}{）}^{\mathbf{T}}{\mathbf{\delta }}^{out}=（{\mathbf{A}}^{\mathbf{h}}{)}^{\mathbf{T}}（{\mathbf{a}}^{\mathbf{o}\mathbf{u}\mathbf{t}}-\mathbf{y}）\odot {\mathbf{\varphi }}^{{}^{\prime }}({\mathbf{Z}}^{(\mathbf{o}\mathbf{u}\mathbf{t})})$$

这里我们可以类比求偏导的方式求${\mathbf{Z}}^{(out)}$ 对$W^{out}$的偏导数，按理说应该是${\mathbf{A}}^h$,那为啥是 $({\mathbf{A}}^{\mathbf{h}}{)}^{\mathbf{T}}$?思考一下，如果纠一下细节，确实是$({\mathbf{A}}^{\mathbf{h}}{)}^{\mathbf{T}}$！这是因为矩阵的乘法所导致：${\mathbf{Z}}^{(out)}$ = ${\mathbf{A}}^{\mathbf{h}}{\mathbf{W}}^{\mathbf{o}\mathbf{u}\mathbf{t}}$，我们可以举个具体的例子：影响${\mathbf{W}}^{out}$第一行第二个的元素其实是${\mathbf{A}}^h$中的第二行第一个元素,也就是$\mathbf{A}(m,n)$---->$\mathbf{W}(n,m)$,所以$\mathbf{A}$矩阵要转置（这里不理解也无所谓，可以选择记住或者跳过）。

---

下面我们谈谈如何求$\frac{\partial J(\mathbf{W})}{\partial w_{m,h}^{(h)}}$（建议先把上面关于$\frac{\partial J(\mathbf{W})}{\partial w_{h,t}^{(out)}}$弄清楚一些）：

我们上面成功的推导出来了$\frac{\partial J(\mathbf{W})}{\partial w_{m,h}^{(h)}}$，并且用我们定义了一个叫做误差项的量，我们算法的名称叫做误差逆向传播算法，故名思义，就是将误差进行逆向传播。既然我们已经成功的计算出来了${\mathbf{\delta }}^{out}$，那么我们可不可以通过${\mathbf{\delta }}^{out}$计算${\mathbf{\delta }}^h$，然后按照同样的步骤计算$\frac{\partial J(\mathbf{W})}{\partial w_{h,t}^{(out)}}$？答案是️，下面我们具体推导说明。

我们已经求得：
$${\delta }_i^{out}=\frac{\partial J(\mathbf{W})}{\partial z_i^{(out)}}=\frac{\partial J(\mathbf{W})}{\partial a_i^{(out)}}{\varphi }^{{}^{\prime }}(z_i^{(out)})$$
目标是(为一般起见我们用i，j进行区分)：
$${\delta }_j^h=\frac{\partial J(\mathbf{W})}{\partial z_j^{(h)}}$$
如果将目标与已求联系，在求偏导过程中引入$z_i^{(out)}$(已用蓝色框标明)：
$${\delta }_j^h=\frac{\partial J(\mathbf{W})}{\partial z_i^{(out)}}\frac{\partial z_i^{(out)}}{\partial z_j^{(h)}}={\delta }_i^{out}\frac{\partial z_i^{(out)}}{\partial z_j^{(h)}}$$
${\delta }_i^{out}$为已知项，现在则需要求：
$$\frac{\partial z_i^{(out)}}{\partial z_j^{(h)}}$$

那$z_i^{(out)}$又与$z_i^{(h)}$有什么关系️？

回答这个问题并不难，但是需要你对正向传播激活神经网络有充分的了解。$z_i^{(h)}$通过激活函数得到$a_i^{(h)}$，而$a_i^{(h)}$又通过和权重的结合得到$z_i^{(out)}$（可以回头看看第一步：正向传播）。

所以：
$$\frac{\partial z_i^{(out)}}{\partial z_j^{(h)}}=\frac{\partial z_i^{(out)}}{\partial a_j^{(h)}}\frac{\partial a_j^{(h)}}{\partial z_j^{(h)}}=w_{j,i}^{(out)}{\varphi }^{{}^{\prime }}(z_j^{(h)})$$

整理以上式子有：
$${\delta }_j^h={\delta }_j^{out}{w}_{j,i}^{(out)}{\varphi }^{{}^{\prime }}(z_j^{(h)})$$
用向量以及哈达玛运算符的形式表达：
$${\mathbf{\delta }}^{\mathbf{h}}={\mathbf{\delta }}^{\mathbf{o}\mathbf{u}\mathbf{t}}({\mathbf{w}}^{(\mathbf{o}\mathbf{u}\mathbf{t})}{)}^{\mathbf{T}}\odot {\mathbf{\varphi }}^{{}^{\prime }}({\mathbf{z}}^{(\mathbf{h})})$$
至此，我们得到${\mathbf{\delta }}^h$也就是损失函数关于${\mathbf{z}}^{(h)}$的偏导数，但是我们最终的目的是其关于权重的偏导数，考虑到${\mathbf{Z}}^{(h)}$ = ${\mathbf{A}}^{\mathbf{o}\mathbf{u}\mathbf{t}}{\mathbf{W}}^{\mathbf{h}}$,所以：

$$\frac{\partial J(\mathbf{W})}{\partial {\mathbf{W}}^{(\mathbf{h})}}=（{\mathbf{A}}^{\mathbf{i}\mathbf{n}}{）}^{\mathbf{T}}{\mathbf{\delta }}^h$$

得到这个结果的方式和我们算$\frac{\partial J(\mathbf{W})}{\partial {\mathbf{W}}^{(\mathbf{o}\mathbf{u}\mathbf{t})}}$相同，可以翻上去回看。

---

4.关于偏置项的梯度

上面我们已经推导出损失函数关于层与层之间权重的偏导数，但是不要忘记了偏置向量的作用。我们在一开始介绍到：在实际操作中偏置单元更改为单独的偏置向量，那么损失函数关于偏执向量的梯度如何求解？

我先把结果写下：
$$\frac{\partial J(\mathbf{W})}{\partial {\mathbf{b}}^{(\mathbf{o}\mathbf{u}\mathbf{t})}}={\mathbf{\delta }}^{out}$$
$$\frac{\partial J(\mathbf{W})}{\partial {\mathbf{b}}^{(\mathbf{h})}}={\mathbf{\delta }}^h$$
即：
$$\frac{\partial J(\mathbf{W})}{\partial \mathbf{b}}=\mathbf{\delta }$$

可以看到损失函数关于偏置向量的偏导数是其所在层的误差向量，这里我做一下简单的说明（其实大家可以当作练习自己推导一番，和上面的推导类似并且要简单，检验下自己是否学会）

我们从就从输出层下手进行推导，我们已知：

$${\delta }_i^{out}=\frac{\partial J(\mathbf{W})}{\partial a_i^{(out)}}\frac{\partial a_i^{(out)}}{\partial z_i^{(out)}}$$

又$z_i^{(out)}$又取决于$b_i^{(out)}$,所以再次在上面的式子中设法添加$b_i^{(out)}$项：
$$\frac{\partial J(\mathbf{W})}{\partial b_i^{(out)}}=\frac{\partial J(\mathbf{W})}{\partial a_i^{(out)}}\frac{\partial a_i^{(out)}}{\partial z_i^{(out)}}\frac{\partial z_i^{(out)}}{\partial b_i^{(out)}}={\delta }_i^{out}\frac{\partial z_i^{(out)}}{\partial b_i^{(out)}}$$
而$\frac{\partial z_i^{(out)}}{\partial b_i^{(out)}}=1$，所以：
$$\frac{\partial J(\mathbf{W})}{\partial b_i^{(out)}}={\delta }_i^{out}$$
于是得证，至于其他的层可以类比得到最终结果：

$$\frac{\partial J(\mathbf{W})}{\partial \mathbf{b}}=\mathbf{\delta }$$

---

5.误差逆向传播公式总结

$$\frac{\partial J(\mathbf{W})}{\partial {\mathbf{W}}^{(\mathbf{o}\mathbf{u}\mathbf{t})}}=（{\mathbf{A}}^{\mathbf{h}}{）}^{\mathbf{T}}{\mathbf{\delta }}^{out}$$

$$\frac{\partial J(\mathbf{W})}{\partial {\mathbf{W}}^{(\mathbf{h})}}=（{\mathbf{A}}^{\mathbf{i}\mathbf{n}}{）}^{\mathbf{T}}{\mathbf{\delta }}^h$$

$$\frac{\partial J(\mathbf{W})}{\partial \mathbf{b}}=\mathbf{\delta }$$

至此我们已经把误差逆向传播算法所需的公式推导并且总结完毕，充分理解好这些公式将有助于对这个算法的认识。其实，我们回过头来看，这里面用的最最核心的就是链式求导法则，所以我觉得要真正的弄明白这个算法：首先要对整个神经网络的传播过程以及各个符号有充分的认识并掌握熟练，其次要会利用链式求导法则进行梯度的求解，最后就是用代码实现

---

5.梯度检测

代码如下（示例）：
未完待续！

6.初始化的重要性

代码如下（示例）：
未完待续！

7.代码实现

具体代码请参考：我的另一篇文章（包含代码注释）

---

总结

以上是我在学习BP神经网络的个人理解，上面的推导数学形式偏多，所以本文章适合数学基础相对较好的而且强烈想弄清楚BP算法的一些公式由来的人参考。另外上文可能有错误，还望各位多多包含，希望找到的朋友可以在评论区留言告诉我好让我及时更改。