关于强化学习中Q-learning和DQN的原理以及在论文中应用
本文中提到的论文应用环境以及代码均来自论文《Spectrum Sharing in Vehicular Networks Based on Multi-Agent Reinforcement Learning》,对于应用场景和其他公式的分析见我的此篇文章
强化学习的基本概念:
强化学习的主体:环境、代理agent
强化学习中的数据量:状态state、动作/行为action、奖励reward
强化学习的目标:找到能使长期累计奖励(某时刻到结束所有奖励的总和)最大化的策略
代理通过与环境进行数据信息的交互进行学习,机器需要通过尝试来发现各个动作产生的结果,而没有训练数据告诉机器应当做哪个动作
类比:强化学习中的“策略”相当于监督学习中的分类器(离散)或者回归器(连续),模型形式没有差别,但是在强化学习中没有监督学习中的有标记样本,只有等到最终的结果揭晓,才能通过“反思"之前动作是否正确来进行学习,因此强化学习在某种程度上可以看作具有”延迟标记信息“的监督学习问题
策略/决策函数π
在代理与环境进行交互的过程中我们期望代理可以学习到最终能完成我们目标的策略(policy),对这个策略进行数据抽象可以抽象为函数,在数学上,这个函数表示如下,函数是个概率密度函数

状态转移函数p
另外一个概念叫做状态转移概率函数,状态转移是随机的(马尔可夫状态转移的随机性),其随机性是从环境里来的,将状态转移函数使用p函数进行表示

对上述式子中的元素进行解释,其中大写的A和S 表示随机变量,而小写的a和s表示所取到的具体的值
关于状态S和动作A的随机性:
- 动作的随机性:动作A根据policy函数π随机抽样得到的
- 状态转移的随机性:在agent做出动作后,环境生成的下一个状态S具有随机性,根据p函数进行随机抽样
累计奖励值U
表示的为从当前时刻到最终任务结束累计的奖励值的总和,未来奖励的累计总和
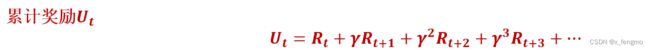
- 其中是指贴现率(0≦≦1),考虑未来的奖励,但是越久远的奖励在考虑其中时占比应当适当的减小。是一个超参数
越久远的应该占比越小是因为,如果很久之后的未来某次操作获得的奖励很大,但是中间过程的某一部失败率很大,那么可能会导致平均下来最终的结果并不理想,所以对于久远之后的奖励应该慎重考虑
此处放置网上搜索到的贴现率的定义:贴现率:又称“折现率”。指今后收到或支付的款项折算为现值的利率
通俗的讲,2003年的10块钱和现在(2023年)的10块钱能买的东西价值不一样了,那么可能现在(2023年)和20年后(2043年)的10块钱所能购买的东西的价值也不一样了
- 对于任意的未来时刻i的奖励,会取决于状态和动作,所以就和t时刻开始未来所有的状态和动作都有关
- 状态是随机变量,概率密度为( ′ | , )= ( ′ = ′ | = , = ),动作是随机变量,概率密度为( | ) = ( = | = ),所以也是随机变量
两种价值函数
在模型已知时,对任何策略能估计出该模型带来的期望累计奖励,以此来进行策略评估
动作价值函数 Action-value function
![]()
- 与, , 有关,期望将未来的动作和状态都消除了,只留下状态和动作两变量
- 含义:当处于状态s时, 给所有动作a打分
- 与, 有关,与a无关,期望将所有A都考虑其中,所以函数V与A无关
- 在使用某个决策的时候,评价当前状态(快赢了or快输了),状态s越好, ()越大
- () 还可以评价决策的好坏,越好, (())越大(期望/均值)
两类学习方法
在对某个策略的累计奖励进行评估后,若发现其并非最优策略,则希望对其进行改进,下面是两种改进算法。算法的分类主要有基于策略(Policy-Based)和基于数值(Value-Based):最终目标都是最大化整体奖励,找到最优的策略。
基于决策略Policy-Based reinforcement learning
→ 每一步选择按照决策函数选择,目标函数:优化决策函数(概率),最大化奖励的期望值
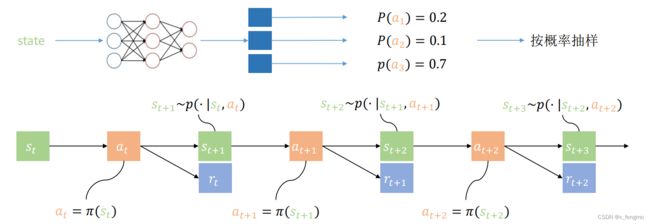
参考文章指路
基于数值Value-Based reinforcement learning
→ 每一步选择按照最大未来奖励选择,目标函数:最大化未来累计奖励函数
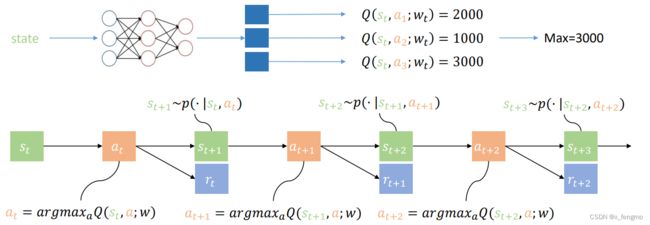
参考文章指路
算法
以上为强化学习的基础知识的铺垫,下面将是q-learning、DQN和double DQN
这三种算法都是上述提到的value-based算法
q-learning
Q-Learning的核心主要为Q-Table,通过判断每一步action的value来进行下一步的动作,以一个简单的左右平移为例

通过选择数值较大的动作作为下一步的动作
-贪心算法:一般情况下,为了避免局部最优情况,从而进行更多的探索,会设置一个概率值,使算法以1-概率按照表格中的数值选择最大,以概率随机进行选择,这就是-贪心算法(比如在论文中选择的是线性退火算法)。
若奖励值的不确定性较大,例如概率分布较宽时,需要更多的探索,此时需要较大的值;若奖励值的不确定性较小,例如概率分布比较集中时,少量的探索就可以得到很好的近似真实奖励,此时需要的值较小。通常令去一个比较小的常数,如0.1或者0.01.然而,若果尝试的次数非常大,那么在一段时间后,单次奖励值可以很好的近似出来,不再需要探索,这种情况下可以让随着尝试次数的增加而逐步减小,例如令=1/√t。
def predict(sess, s_t, ep, test_ep = False):
n_power_levels = len(env.V2V_power_dB_List)
if np.random.rand() < ep and not test_ep:
pred_action = np.random.randint(n_RB*n_power_levels)
else:
pred_action = sess.run(g_q_action, feed_dict={x: [s_t]})[0]
return pred_action
DQN
最原始的Q-learning算法在执行过程中始终需要一个Q表进行记录,当维数不高的时候Q表尚可满足需求,但是遇到指数级别的维数时,Q表的效率就十分有限
DQN使用深度神经网络作为值函数的近似工具,用神经网络去近似Q函数(根据Q对求最大化得到的最优动作价值函数Q),将这个神经网络记为Q*(s,a;w),其中神经网络的参数为w,输入是状态s,输出为对所有可能动作的打分,每一个动作对应一个分数,通过奖励值来学习神经网络。这个神经网络给动作的打分会逐步改进,越来越准。
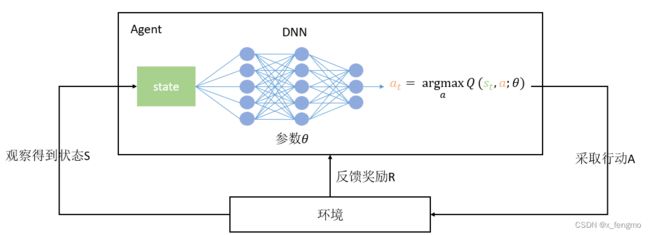
DQN对于policy的迭代更新过程(来自李宏毅老师ppt)(右边为DQN原理与现实问题的联想)
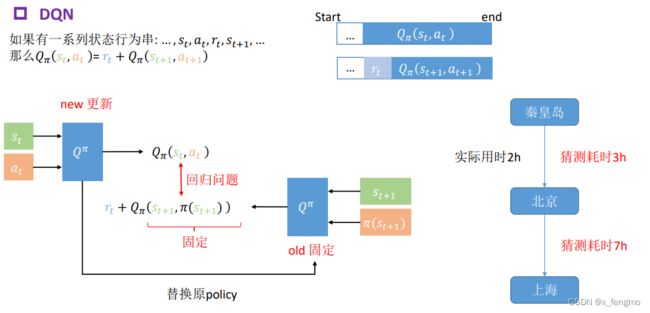
如果我想从秦皇岛去上海,途中经过北京,对于初始(或者旧的决策)我得出,从秦皇岛到北京可能需要3小时,从北京到上海可能需要7小时,那么我可以得到秦皇岛到上海的Q函数为10小时。
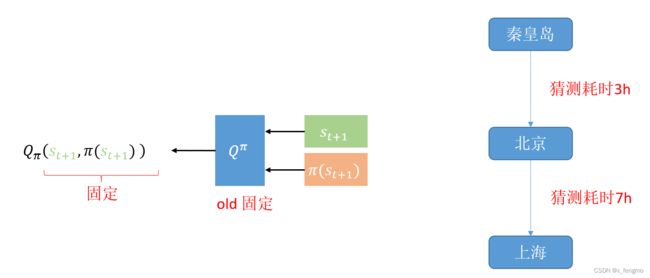
但是我现在坐车从秦皇岛到北京,发现实际上只用了2小时,也就是我得到了旅行途中一部分真实的时间,因为得到了一部分真实的数据,所以我打算对我原来的决策信息进行更新,现在由我得到的真实信息秦皇岛-北京的2小时,和我估计的北京-上海的7小时,我得到了一个比之前的决策信息可靠一点的Q函数9小时。
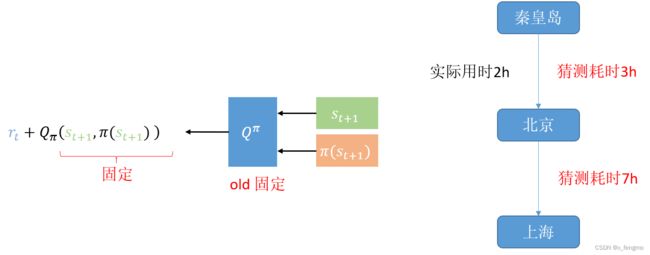
使用这个新的Q函数对神经网络进行训练,这是一个回归问题
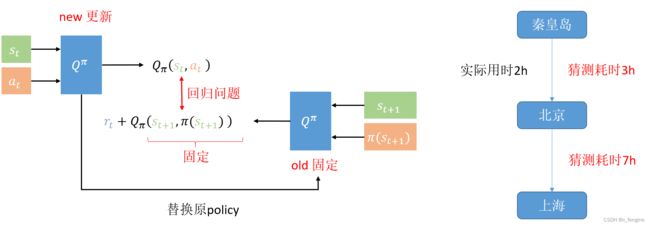
double DQN
Double DQN和DQN之前的区别主要在于训练过程中的目标函数中(_+1) 因为是由决策函数得出的,所以也就是max (_+1, a)
DQN的目标函数为

double DQN的目标函数为

也就是使用两个Q函数,选择action的Q函数和计算value的Q函数不是同一个函数,避免过估计现象发生
具体原理参考此文
下面解析一下论文源码与此相关的部分
下面部分为搭建神经网络的部分,这里主要记录一下优化器RMSProp optim = tf.train.RMSPropOptimizer(learning_rate=0.001, momentum=0.95, epsilon=0.01).minimize(g_loss)

原理见文章
# main_marl_train.py中
# 搭建神经网络
n_hidden_1 = 500
n_hidden_2 = 250
n_hidden_3 = 120
n_input = len(get_state(env=env))
n_output = n_RB * len(env.V2V_power_dB_List)
g = tf.Graph()
with g.as_default():
# ============== Training network ========================
x = tf.placeholder(tf.float32, [None, n_input])
w_1 = tf.Variable(tf.truncated_normal([n_input, n_hidden_1], stddev=0.1))
w_2 = tf.Variable(tf.truncated_normal([n_hidden_1, n_hidden_2], stddev=0.1))
w_3 = tf.Variable(tf.truncated_normal([n_hidden_2, n_hidden_3], stddev=0.1))
w_4 = tf.Variable(tf.truncated_normal([n_hidden_3, n_output], stddev=0.1))
b_1 = tf.Variable(tf.truncated_normal([n_hidden_1], stddev=0.1))
b_2 = tf.Variable(tf.truncated_normal([n_hidden_2], stddev=0.1))
b_3 = tf.Variable(tf.truncated_normal([n_hidden_3], stddev=0.1))
b_4 = tf.Variable(tf.truncated_normal([n_output], stddev=0.1))
layer_1 = tf.nn.relu(tf.add(tf.matmul(x, w_1), b_1))
layer_1_b = tf.layers.batch_normalization(layer_1)
layer_2 = tf.nn.relu(tf.add(tf.matmul(layer_1_b, w_2), b_2))
layer_2_b = tf.layers.batch_normalization(layer_2)
layer_3 = tf.nn.relu(tf.add(tf.matmul(layer_2_b, w_3), b_3))
layer_3_b = tf.layers.batch_normalization(layer_3)
y = tf.nn.relu(tf.add(tf.matmul(layer_3, w_4), b_4))
g_q_action = tf.argmax(y, axis=1) #取出y中元素最大值所对应的索引
# compute loss
g_target_q_t = tf.placeholder(tf.float32, None, name="target_value")
g_action = tf.placeholder(tf.int32, None, name='g_action')
action_one_hot = tf.one_hot(g_action, n_output, 1.0, 0.0, name='action_one_hot')
q_acted = tf.reduce_sum(y * action_one_hot, reduction_indices=1, name='q_acted')
g_loss = tf.reduce_mean(tf.square(g_target_q_t - q_acted), name='g_loss')
optim = tf.train.RMSPropOptimizer(learning_rate=0.001, momentum=0.95, epsilon=0.01).minimize(g_loss)
# ==================== Prediction network ========================
x_p = tf.placeholder(tf.float32, [None, n_input])
w_1_p = tf.Variable(tf.truncated_normal([n_input, n_hidden_1], stddev=0.1))
w_2_p = tf.Variable(tf.truncated_normal([n_hidden_1, n_hidden_2], stddev=0.1))
w_3_p = tf.Variable(tf.truncated_normal([n_hidden_2, n_hidden_3], stddev=0.1))
w_4_p = tf.Variable(tf.truncated_normal([n_hidden_3, n_output], stddev=0.1))
b_1_p = tf.Variable(tf.truncated_normal([n_hidden_1], stddev=0.1))
b_2_p = tf.Variable(tf.truncated_normal([n_hidden_2], stddev=0.1))
b_3_p = tf.Variable(tf.truncated_normal([n_hidden_3], stddev=0.1))
b_4_p = tf.Variable(tf.truncated_normal([n_output], stddev=0.1))
layer_1_p = tf.nn.relu(tf.add(tf.matmul(x_p, w_1_p), b_1_p))
layer_1_p_b = tf.layers.batch_normalization(layer_1_p)
layer_2_p = tf.nn.relu(tf.add(tf.matmul(layer_1_p_b, w_2_p), b_2_p))
layer_2_p_b = tf.layers.batch_normalization(layer_2_p)
layer_3_p = tf.nn.relu(tf.add(tf.matmul(layer_2_p_b, w_3_p), b_3_p))
layer_3_p_b = tf.layers.batch_normalization(layer_3_p)
y_p = tf.nn.relu(tf.add(tf.matmul(layer_3_p_b, w_4_p), b_4_p))
g_target_q_idx = tf.placeholder('int32', [None, None], 'output_idx')
target_q_with_idx = tf.gather_nd(y_p, g_target_q_idx)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
if语句中为double DQN算法,第一行代码pred_action为下图中的Q函数,q_t_plus_1为下图中的Q’函数,即使用两个Q函数,选择action的Q函数和计算value的Q函数不是同一个函数,避免过估计现象发生,batch_target_q_t为累计奖励(包含贴现率current_agent.discount)
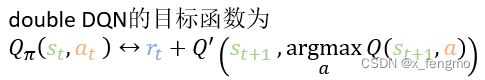
else语句中为DQN算法 q_t_plus_1为决策做出的选择a=(_+1),max_q_t_plus_1为在同一Q函数中选择的Q的最大值,batch_target_q_t为累计奖励(包含贴现率current_agent.discount)

在if…else语句外的最后一行语句通过计算损失函数Loss对神经网络进行更新
def q_learning_mini_batch(current_agent, current_sess):
""" Training a sampled mini-batch """
batch_s_t, batch_s_t_plus_1, batch_action, batch_reward = current_agent.memory.sample()
if current_agent.double_q: # double DQN
pred_action = current_sess.run(g_q_action, feed_dict={x: batch_s_t_plus_1})
q_t_plus_1 = current_sess.run(target_q_with_idx, {x_p: batch_s_t_plus_1, g_target_q_idx: [[idx, pred_a] for idx, pred_a in enumerate(pred_action)]})
batch_target_q_t = current_agent.discount * q_t_plus_1 + batch_reward
else: # DQN
q_t_plus_1 = current_sess.run(y_p, {x_p: batch_s_t_plus_1})
max_q_t_plus_1 = np.max(q_t_plus_1, axis=1)
batch_target_q_t = current_agent.discount * max_q_t_plus_1 + batch_reward
_, loss_val = current_sess.run([optim, g_loss], {g_target_q_t: batch_target_q_t, g_action: batch_action, x: batch_s_t})
return loss_val
参考文章汇总
Q-learning原理及其实现方法_北木.的博客-CSDN博客_qlearning原理
强化学习入门这一篇就够了!!!万字长文_CC-Mac的博客-CSDN博客_强化学习
Value-Based Reinforcement Learning-DQN_CC-Mac的博客-CSDN博客
Policy-based Reinforcement learning_CC-Mac的博客-CSDN博客
深度强化学习系列(5): Double Q-Learning原理详解_@RichardWang的博客-CSDN博客_double q-learning


