多元线性回归boston房价(吴恩达机器学习笔记)
目录
-
-
-
- 1.多元线性回归
-
- 1.梯度下降法
- 2.正规方程
- 2梯度下降法实践
-
- 1.特征缩放
- 2.学习率(learning rate)
- 3.Boston房价预测
-
-
1.多元线性回归
对房价模型增加更多的特征,如房间数,楼层数等,构成了一个含有多变量的模型,模型中特征为 ( x 1 , x 2 . . . x n ) (x_{1},x_{2}...x_{n}) (x1,x2...xn).

其中n代表特征数量,m代表训练集中的实列数量。
x ( i ) x^{(i)} x(i)代表第i个训练实列。
x j ( i ) x^{(i)}_{j} xj(i)代表特征矩阵中第i行的第j个特征。
多变量的回归的假设h为: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h_{\theta}(x)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n} hθ(x)=θ0+θ1x1+θ2x2+...+θnxn.由于有n+1个参数变量,n个变量,为了简化计算,引入了 x 0 = 1 x_{0}=1 x0=1.则:
X = [ x 0 x 1 x 2 . . . x n ] X=\left[\begin{matrix}x_{0}\\x_{1}\\x_{2}\\...\\x_{n}\end{matrix}\right] X=⎣⎢⎢⎢⎢⎡x0x1x2...xn⎦⎥⎥⎥⎥⎤ θ = [ θ 0 θ 1 θ 2 . . . θ n ] \theta=\left[\begin{matrix}\theta_{0}\\\theta_{1}\\\theta_{2}\\...\\\theta_{n}\end{matrix}\right] θ=⎣⎢⎢⎢⎢⎡θ0θ1θ2...θn⎦⎥⎥⎥⎥⎤
则 h θ ( x ) = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + . . . θ n x n h_{\theta}(x)=\theta_{0}x_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...\theta_{n}x_{n} hθ(x)=θ0x0+θ1x1+θ2x2+...θnxn= θ T X \theta^{T}X θTX
接下来就要 求解 θ \theta θ
1.梯度下降法
构造代价函数 J ( θ 0 , θ 1 , . . . θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_{0},\theta_{1},...\theta_{n})=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2} J(θ0,θ1,...θn)=2m1∑i=1m(hθ(x(i))−y(i))2
运用梯度下降法:
θ j = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 , . . . , θ n ) \theta_{j}=\theta_{j}-\alpha \frac{\partial}{\partial\theta_{j}}J(\theta_{0},\theta_{1},...,\theta_{n}) θj=θj−α∂θj∂J(θ0,θ1,...,θn)
θ j = θ j − α ∂ ∂ θ j 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 \theta_{j}=\theta_{j}-\alpha \frac{\partial}{\partial\theta_{j}}\frac{1}{2m}\sum_{i=1}^{m}({h_{\theta}(x^{(i)})-y^{(i)}})^{2} θj=θj−α∂θj∂2m1∑i=1m(hθ(x(i))−y(i))2
θ j = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_{j}=\theta_{j}-\alpha \frac{1}{m}\sum_{i=1}^{m}({h_{\theta}(x^{(i)})-y^{(i)}})x^{(i)}_{j} θj=θj−αm1∑i=1m(hθ(x(i))−y(i))xj(i)
2.正规方程
正规方程通过是通过对代价函数进行求导,并使其导数为0,来解得 θ \theta θ.假设训练集的特征矩阵为X,训练结果为向量y,则利用正规方程求解出 θ = ( X T X ) − 1 X T y \theta=(X^{T}X)^{-1}X^{T}y θ=(XTX)−1XTy
当特征变量数目小于1万以下时,通常使用正规方程来求解,大于一万则使用梯度下降法。
2梯度下降法实践
1.特征缩放
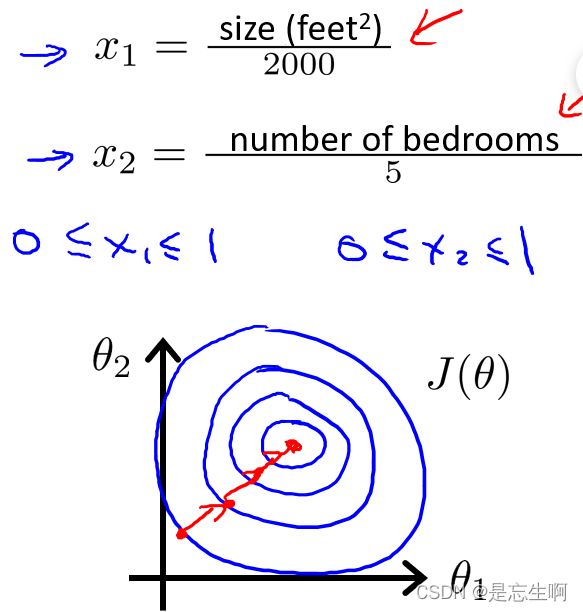
以房价为例,假设我们使用两个特征(房屋的尺寸大小和房间的数量),并且令 θ 0 = 0 \theta_{0}=0 θ0=0,尺寸大小为 0 — 2000 0—2000 0—2000平方尺,而房间数量则是 0 − 5 0-5 0−5间,则以两个参数分别为横纵坐标轴,绘制出代价函数的等高线图。其图像将会是一个很扁的椭圆形,此时进行梯度下降法时,往往需要很多次迭代才能够收敛。

为了解决这个问题:就需要对特征进行缩放,如图:
另一种缩放形式是:
x i = x − u i S i x_{i}=\frac{x-u_{i}}{S_{i}} xi=Six−ui
其中 u i u_{i} ui是所有训练集中的特征 x i x_{i} xi的平均值。 S i S_{i} Si是其标准差,但也可以用极差(最大值见最小值)来代替。
2.学习率(learning rate)
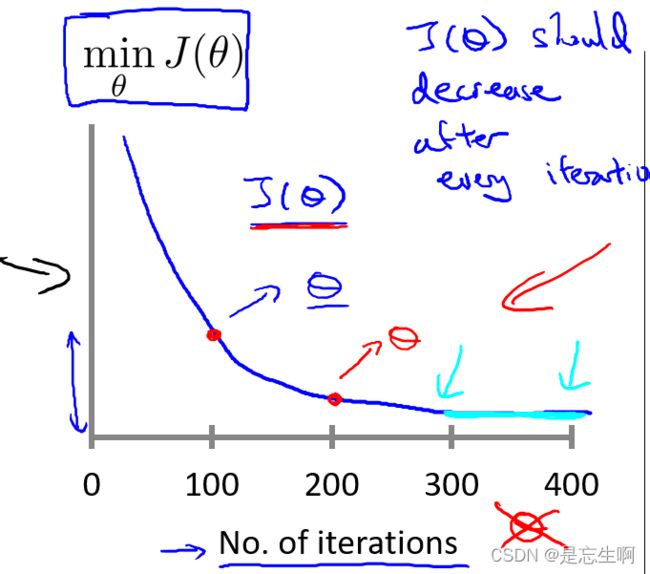
由于梯度下降法收敛所需的迭代次数无法提前预支。通常画出代价函数随迭代次数的图像来观察梯度下降法合适趋于收敛。
当然也可以自带测试收敛,即将代价函数的变化值与某个阈值 w w w(如:0.001)来比较,如果小于该阈值则认为此时收敛。但是选择一个合适的阈值也是比较困,所有更多采用第一种方法。
当代价函数随迭代步数的图像如此变化时,说明此时 α \alpha α偏大,应当选择一个稍微小一点的值。

当 α \alpha α过小时,则梯度下降法会收敛的非常慢,需要很多次迭代才会收敛。
尝试挑选的学习率:……,0.001,0.003,0.1,0.3,1,……
3.Boston房价预测
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt
boston=datasets.load_boston()
x_data=boston.data
y_data=boston.target
#print(boston.feature_names)
print(x_data.shape)
print(y_data.shape)
for i in range(x_data.shape[1]):#对数据进行归一化
x_data[:,i]=(x_data[:,i]-x_data[:,i].mean())/(x_data[:,i].max()-x_data[:,i].min())
X=np.concatenate((np.ones((x_data.shape[0],1)),x_data),axis=1)#添加偏置项
Y=y_data.reshape(-1,1)
print(X.shape,Y.shape)
print(X[:5,0:])
(506, 13)
(506,)
(506, 14) (506, 1)
[[ 1. -0.0405441 0.06636364 -0.32356227 -0.06916996 -0.03435197
0.05563625 -0.03475696 0.02682186 -0.37171335 -0.21419304 -0.33569506
0.10143217 -0.21172912]
[ 1. -0.04030818 -0.11363636 -0.14907546 -0.06916996 -0.17632728
0.02612869 0.10633469 0.1065807 -0.32823509 -0.31724648 -0.06973762
0.10143217 -0.09693883]
[ 1. -0.0403084 -0.11363636 -0.14907546 -0.06916996 -0.17632728
0.17251688 -0.07698147 0.1065807 -0.32823509 -0.31724648 -0.06973762
0.09116942 -0.23794325]
[ 1. -0.0402513 -0.11363636 -0.32832766 -0.06916996 -0.19896103
0.13668626 -0.23455099 0.20616331 -0.28475683 -0.35541442 0.02600706
0.09570823 -0.26802051]
[ 1. -0.03983903 -0.11363636 -0.32832766 -0.06916996 -0.19896103
0.16523579 -0.14804224 0.20616331 -0.28475683 -0.35541442 0.02600706
0.10143217 -0.20207128]]
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) − y ( i ) ) ) 2 J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)}-y^{(i)}))}^{2} J(θ)=2m1i=1∑m(hθ(x(i)−y(i)))2
∑ i = 1 2 m ( h θ ( x ( i ) ) − y ( i ) ) 2 = ( y − x θ ) T ( y − x θ ) \sum_{i=1}^{2m}(h_{\theta}(x^{(i)})-y^{(i)})^{2}=(y-x\theta)^{T}(y-x\theta) i=1∑2m(hθ(x(i))−y(i))2=(y−xθ)T(y−xθ)
公式: ( A + B ) T = A T + B T (A+B)^{T}=A^{T}+B^{T} (A+B)T=AT+BT
( A B ) T = B T A T (AB)^{T}=B^{T}A^{T} (AB)T=BTAT
∂ J ( θ ) ∂ θ = ∂ ( y − x θ ) T ( y − x θ ) ∂ θ \frac{\partial J(\theta)}{\partial \theta}=\frac{\partial (y-x\theta)^{T}(y-x\theta)}{\partial \theta} ∂θ∂J(θ)=∂θ∂(y−xθ)T(y−xθ)
= ∂ ( y T y − y T x θ − θ T x T y + θ T x T x θ ) ∂ θ =\frac{\partial (y^{T}y-y^{T}x\theta-\theta^{T}x^{T}y+\theta^{T}x^{T}x\theta)}{\partial \theta} =∂θ∂(yTy−yTxθ−θTxTy+θTxTxθ)
= ∂ y T y ∂ θ − ∂ y T x θ ∂ θ − ∂ θ T x T y ∂ θ + ∂ θ T x T x θ ∂ θ =\frac{\partial y^{T}y}{\partial \theta}-\frac{\partial y^{T}x\theta}{\partial \theta}-\frac{\partial \theta^{T}x^{T}y}{\partial \theta}+\frac{\partial \theta^{T}x^{T}x\theta}{\partial \theta} =∂θ∂yTy−∂θ∂yTxθ−∂θ∂θTxTy+∂θ∂θTxTxθ
分子布局:分子为列向量或者分母为行向量
分母布局:分子为行向量或者分母为列向量
| 分子布局 | 分母布局 | |
|---|---|---|
| ∂ b T A x ∂ x \frac{\partial b^{T}Ax}{\partial x} ∂x∂bTAx | b T A b^{T}A bTA | A T b A^{T}b ATb |
| ∂ X T A X ∂ X \frac{\partial X^{T}AX}{\partial X} ∂X∂XTAX | X T ( A + A T ) X^{T}(A+A^{T}) XT(A+AT) | ( A + A T ) X (A+A^{T})X (A+AT)X |
∂ y T y ∂ θ = 0 \frac{\partial y^{T}y}{\partial \theta}=0 ∂θ∂yTy=0
∂ y T x θ ∂ θ = x T y \frac{\partial y^{T}x\theta}{\partial \theta}=x^{T}y ∂θ∂yTxθ=xTy
应为 θ T x T y \theta^{T}x^{T}y θTxTy为标量
∂ θ T x T y ∂ θ = ( ∂ θ T x T y ) T ∂ θ = ∂ y T x θ ∂ θ = x T y \frac{\partial \theta^{T}x^{T}y}{\partial \theta}=\frac{(\partial \theta^{T}x^{T}y)^{T}}{\partial \theta}=\frac{\partial y^{T}x\theta}{\partial \theta}=x^{T}y ∂θ∂θTxTy=∂θ(∂θTxTy)T=∂θ∂yTxθ=xTy
∂ θ T x T x θ ∂ θ = ( x T x + ( x T x ) T ) θ = 2 x T x θ \frac{\partial \theta^{T}x^{T}x\theta}{\partial \theta}=(x^{T}x+(x^{T}x)^{T})\theta=2x^{T}x\theta ∂θ∂θTxTxθ=(xTx+(xTx)T)θ=2xTxθ
∂ J ( θ ) ∂ θ = X T X θ − X T y \frac{\partial J(\theta)}{\partial \theta}=X^{T}X\theta-X^{T}y ∂θ∂J(θ)=XTXθ−XTy
直接令J=0
可直接求解出 θ \theta θ
θ = ( X T X ) − 1 X T Y \theta=(X^{T}X)^{-1}X^{T}Y θ=(XTX)−1XTY
theta=np.random.rand(14,1)
print(theta)
[[0.59826263]
[0.7714136 ]
[0.96782367]
[0.05007622]
[0.28160071]
[0.59145316]
[0.86688075]
[0.32402074]
[0.83781872]
[0.9972824 ]
[0.03729666]
[0.3470009 ]
[0.35738919]
[0.25179409]]
learning_rate=0.0001
epochs=10000
costList=[]
for i in range(epochs):
grad_theta=np.matmul(X.T,np.matmul(X,theta)-Y)
#print(grad_theta.shape)
theta=theta-learning_rate*grad_theta
if(i%10==0):
cost=np.mean(np.square(Y-np.matmul(X,theta)))
costList.append(cost)
ep=np.linspace(0,epochs,1000)
print(costList[-1])
plt.plot(ep,costList)
plt.xlabel('epochs')
plt.ylabel('cost')
plt.show()
21.901811902045843
theta
array([[ 22.53280632],
[ -8.60798018],
[ 4.47504867],
[ 0.50817969],
[ 2.71178142],
[ -8.41145881],
[ 20.00501683],
[ 0.09039972],
[-15.82506381],
[ 6.74485343],
[ -6.25266277],
[ -8.92882317],
[ 3.73796887],
[-19.13688284]])
#正规方程
Xmat=np.matrix(X)
Ymat=np.matrix(Y)
xt=Xmat.T*Xmat
w=xt.I*X.T*Y
w
matrix([[ 22.53280632],
[ -9.60975755],
[ 4.64204584],
[ 0.56083933],
[ 2.68673382],
[ -8.63457306],
[ 19.88368651],
[ 0.06721501],
[-16.22666104],
[ 7.03913802],
[ -6.46332721],
[ -8.95582398],
[ 3.69282735],
[-19.01724361]])
cost=np.mean(np.square(Ymat-Xmat*w))
cost
21.894831181729206