从0开始的CNN学习之路(三)-新疆大学智能制造现代产业学院
目录
前言
一、NN(Neural Network)的由来
1.符号主义
2.连接主义/仿生主义
二、NN(Neural Network)的构造
1.逻辑单元
2.NN(Neural Network)
(1).NN的计算分析
(2).NN的前向传播(Forward propagation)
(3).归一化函数:SoftMax函数
三、BP算法(Backward propagation)
总结
前言
上一章我们讲了CNN训练的原理及其本质,那么这一章我们将正式开始分析神经网络(NN)
在此我先对上一章做一个补充:上一章我说到CNN其实是类似一个y=ax+b的数学模型,只不过实际上这个模型要远远比y=ax+b复杂的多,其实这句话是不严谨的,为了防止对新手的误导,我在此说明一下,CNN是一个数学模型不错,但绝对不是y=ax+b这样的,因为它是一个非线性模型,如果是y=ax+b这样的线性模型,将毫无意义可言,它实际上是一个复杂无比的非线性数学模型,大家一定要注意
一、NN(Neural Network)的由来
上一章,我们讲到了CNN是通过梯度下降的方法来进行模型训练的,其实这个算法早期是用在机器学习中的,当时的问题并不是很复杂,所以可以通过人为的使用这些数学方法来进行梯度计算训练,但是随着深度学习的发展,问题逐渐变得复杂,人们逐渐意识到这些问题通过人为计算已经难以得出结果,于是从这一刻起,这门学科出现了分支:
1.符号主义
即早期的人为计算,人工经验
2.连接主义/仿生主义
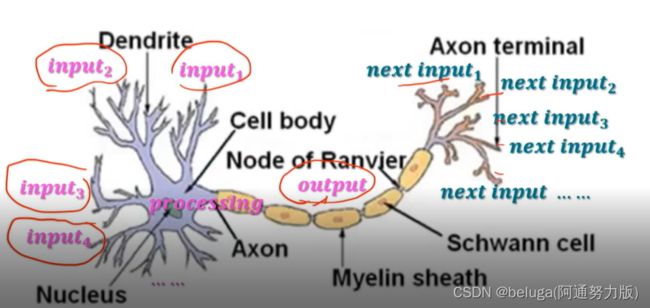
当人们发现问题复杂到难以人工解决的时候,变有了模仿自然的想法,他们觉得可以通过自然规律来解决这个问题,于是他们通过模仿人类大脑的神经元,创建了神经网络(NN),并由此衍生出一门学科---heural science(神经仿生学),这门学科,大家感兴趣的可以下去自行查看,这里不多赘述
如上图所示, 当时人们觉得大脑神经元有很多个突触接收信号,同时又有一个输出,便觉得这种方式和他们处理机器学习的方式很像,便进行模仿,创建了神经网络(NN)
注:由于当时并不是很清楚人的大脑神经元构造,所以这里只是他们自认为是这种结构,进而大致模仿出NN,实际上有可能大不一样(这里就是后话啦,哈哈哈...)
二、NN(Neural Network)的构造
1.逻辑单元
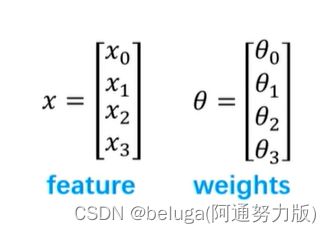
如上图所示,便是神经网络的一个基本逻辑单元,多个基本逻辑单元组合在一起便是一个神经网络,其中每一个圆圈便是一个神经元
现在我们对其进行分析:首先x0便是我们上一章提到的偏置,x1~x3便是我们的输入,θ便是我们的权重,接下来我们让x与θ相乘,得到y=x0*θ0+...+x3*θ3,而y再经过一层激活函数f()得到f(y),便是我们最终的输出结果hθ(x)
其中激活函数f()的作用是将线性模型y=x*θ进行非线性转换,增加NN的鲁棒性,至此大家应该就能明白为什么我在前言中说CNN其实是一种非线性数学模型了
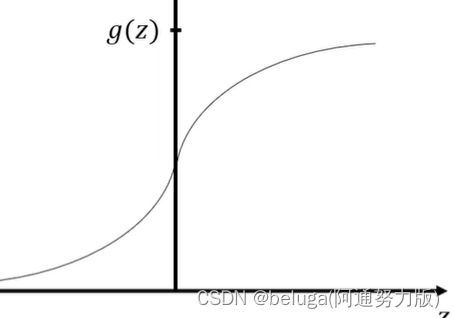
如上图所示,便是激活函数的一种---sigmoid函数,该函数的值范围在0~1之间,单调递增
注:每一个逻辑单元是必定有一个激活函数的,通常来说,大多数神经网络的逻辑单元都用的同一种激活函数,但是也有部分论文中使不同的逻辑单元使用不同的激活函数
2.NN(Neural Network)
(1).NN的计算分析
上面我们讲解了神经网络的基本构成---逻辑单元,那么我们现在就用多个逻辑单元来构造一个简单的神经网络
如上图,我们使用了3+1=4个逻辑单元搭建了一个非常简单的神经网络,其中第一层神经元(Layer 1)我们将其叫做输入层,用来输入我们的数据,如图片等,第二层我们将输入的图片进行了特征提取并进行了非线性转换,我们将其叫做隐藏层,而第三层则是我们将特征进行了计算得出了结果,我们将其叫做输出层
其中,中间的隐藏层在代码中的表示实际为一个4*3的矩阵,其中4代表的是输入维度(3个输入+一个偏置).3则代表的是隐藏层维度(a1,a2,a3)
注:θ12(1)表示第一层网络中第二个输入x2对第二层网络中第一个输出的权重a1(2),(1)代表第一次网络(Layer 1),2代表第二个输入x2,1代表第二层网络的第一个输出a1(2),别的参数以此类推
(2).NN的前向传播(Forward propagation)
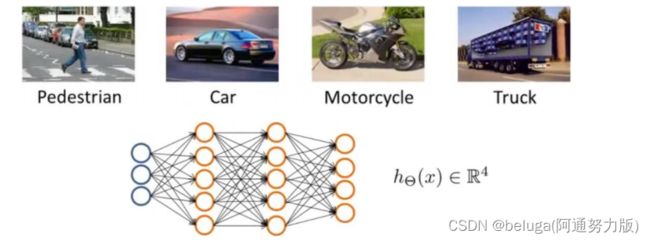
上面我们以及分析了神经网络的从输入到输出的计算过程,其实这个过程便是神经网络的前向传播过程,在这里我们将借助一个目标分类示例来帮助大家进一步感受神经网络的前向传播
如图所示,有一张图片,我们将其放入神经网络中,要求神经网络进行分类检测,判断图片内容是人,车,摩托和卡车中的哪一类
首先,我们将图片通过输入层输入进去后,经过中间两层隐藏层特征提取和非线性转换后,在第四层输出层进行了四个结果输出,这四个结果分别代表图片中的内容是人,车,摩托和卡车的概率值,这四个概率值的总和等于1,而这四个类别的概率值哪个最大,网络便认为图片内容是哪一类,这便是神经网络的前向传播
其中,四个类别的概率值之和是如何等于一的,这就要引出我们下面要讲到的内容---归一化函数:Soft Max函数了
(3).归一化函数:SoftMax函数
Softmax函数是用于多类分类问题的激活函数,在多类分类问题中,超过两个类标签则需要类成员关系。对于长度为K的任意实向量,Softmax函数可以将其压缩为长度为K,值在 [0,1]范围内,并且向量中元素的总和为1的实向量
下面我对上面的话进行一番解释:
Softmax函数与正常的max函数不同:max函数仅输出最大值,但Softmax函数确保较小的值具有较小的概率,并且不会直接丢弃。我们可以认为它是 arg max函数的概率版本或“soft”版本。Softmax函数的分母结合了原始输出值的所有因子,这意味着Softmax函数获得的各种概率彼此相关。
注:
1.Softmax函数设计的初衷,是希望特征对概率的影响是乘性的。同时Softmax函数负输入的梯度为零,这意味着对于该区域的激活,权重不会在反向传播期间更新,因此会产生永不激活的死亡神经元。
2.分类任务一般使用逻辑斯蒂损失函数或者交叉熵损失韩式,回归任务一般使用MSE损失函数
3.Softmax函数也是激活函数的一种
三、BP算法(Backward propagation)
上面我们已经讲了神经网络的前向传播过程,那么按照我们从第二章学到的知识,我们已经能够通过前向传播得到的结果与真实值对比,得到损失函数来评判模型的好坏了,所以接下来我们就是要用梯度下降算法来训练模型求得最优解了,但是前面我们说到神经网络是用来解决人们无法解决的复杂问题的,所以它的损失函数的梯度下降一定不是我们认为能够解出来的,因此我们需要用到BP(反向传播)算法
没错,BP算法就是用来解决神经网络的梯度下降问题的,它的核心思想则是链式法则
首先,我们先用一个非常简单的神经网络来帮助大家理解反向传播的链式法则思想
具体如图笔记所示,大家看完这个后想必已经大概了解了,那么接下来,我们再用一个稍微复杂的神经网络进行实际分析
如图所示,这是该神经网络的前向传播过程,我已经非常详细的写出来了,大家也可以自己算一遍,接下来我们看它的反向传播过程
看到这里相比大家已经理解的差不多了,没错,反向传播之所以是从后往前的,便是因为每一层的值之间是一个复合函数的关系,因此可以从后往前不断推导出前面的梯度
希望这份手写的笔记能够给大家带来更深的理解,如果有什么问题,欢迎评论区留言
总结
感谢大家的观看