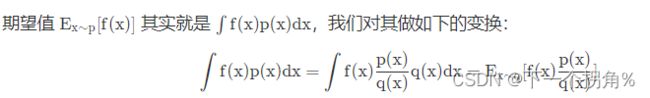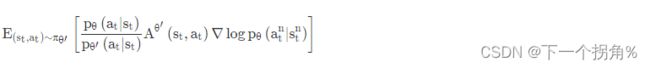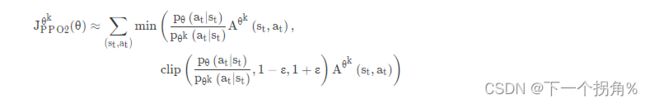强化学习--PPO（近端策略优化）

On-policy 和 Off-policy

1. 策略梯度 是一个 on-policy 的算法。

       因为 是 一个 actor 按照 policy 去和 env 互动，得到一系列轨迹，根据 它 互动 的信息（s,a,r）按照 策略梯度 的 公式 更新 策略π 的参数θ​ 。【学习和交互是同一个agent】

     

上一章 计算 的 策略梯度。 policy πθ​  采样出来轨迹τ的概率  pθ​(τ)， 在参数更新后，就发生了改变pθ​(τ)这个概率就不对了，所以采样的数据 也不能再继续使用了，所以要重新采集。这就解释了上一章 说的 为什么  采样一次更新一次。

2. 对于上述 问题 ，会进行很多次采样 的 改进 -》off-policy。

 用一个 固定的  policy ，actor θ′ 去跟环境做互动，收集数据， 去训练更新 另一个 policy  actor θ

 具体做法：

【重要性采样】-- 但是 pθ​(at​∣st​) 跟 pθ′​(at​∣st​) 这两个分布差太多的话，重要性采样的结果就会不好。因为 方差 var 差的大 

重要性采样 推导公式：

  θ′  和  θ 分布不一样， θ′ 可以是任意分布，所以有个 修正 “重要性权重”   pθ(τ)/pθ​'(τ)​  [ 重要性权重就是某一个轨迹 τ 用 θ 算出来的概率  除以  这个轨迹 τ 用 θ′ 算出来的概率 ] 。

3.对于 上一个 图片中 R（ τ ）是一个回合的奖励，上一章的 tip 中  改进了 这个奖励 权重 ，为了削弱 采样 方差大的问题 引入 baseline ，对于不同动作 采取不同权重而不是整个回合的奖励权重。得到下图：

 （1）第一个红线 出应该是 θ′ ，因为是 用的 θ′ 和环境交互，采集的reward 应该是θ′ 产生的

（2）第二个红线 假设了 模型 θ 的时候，看到 s_t 的概率，跟模型是 θ′ 的时候，你看到 s_t​ 的概率是差不多的，即pθ​(st​)=pθ′​(st​)。直观原因解释是算不出来，所以无视？？这个有一些问题

（3）得到新的  目标函数

总结：

1. θ′ 去跟环境做互动，采样出 s_t​、a_t

2.计算 s_t 跟 a_t​ 的 advantage  奖励

3.乘上  pθ​(at​∣st​) \ pθ′​(at​∣st​) 。知道 θ 和 θ′ 的参数 ，就是两个网络 ，输入  s_t ，输出 每一个 a_t 的概率是多少。

4.求梯度  更新 θ 

 PPO

【由于在 PPO 中θ′ 是 θold​，即 behavior policy 也是 θ，所以 PPO 是 on-policy 的算法。那不就是一个θ　了吗？？】

    出现的原因：

    针对上面  重要性采样  的 问题 -- pθ​(at​∣st​) 跟 pθ′​(at​∣st​) 不能差太多 。怎么 避免差的多-》ppo。

    解决方案：

在 训练  的时候明天添加了 一个  约束，约束是 θ 跟θ′ 输出的动作的 KL 散度(KL divergence)，这一项的意思就是要衡量说θ 跟 θ′ 有多像。所以 PPO的优化目标函数添加一项，变为

 下面 的 TRPO 是 PPO 的前身，此处KL散度 没有在优化目标函数中直接计算，而是一个额外约束，基于梯度优化的时候，有约束的很难处理

（1）KL散度：不是计算的　θ 和 θ′　参数上的距离，而是　动作　上的距离。输入：相同状态，输出：动作空间的概率分布，计算两个　概率分布　之间的KL散度。把　不同的状态　输出　的这　两个分布　的 KL 散度　平均　起来就是所指的两个 actor 间的 KL 散度。

变种１　PPO１－(PPO-Penalty)

（1）先初始化一个 policy 的参数 \theta^0 θ0。然后在每一个迭代里面，你要用参数 \theta^k θk，\theta^k θk 就是你在前一个训练的迭代得到的 actor 的参数，你用 \theta^k θk 去跟环境做互动，采样到一大堆状态-动作的对。

（2）  KL散度前面系数 β 可以动态调整：

 

   先设一个你可以接受的 KL 散度的最大值。假设优化完这个式子以后，你发现 KL 散度的项太大，那就代表说后面这个惩罚的项没有发挥作用，那就把 β 调大，让约束增强。当优化完，小于最小值，说明θ 跟 θk 很像，要减弱 约束。

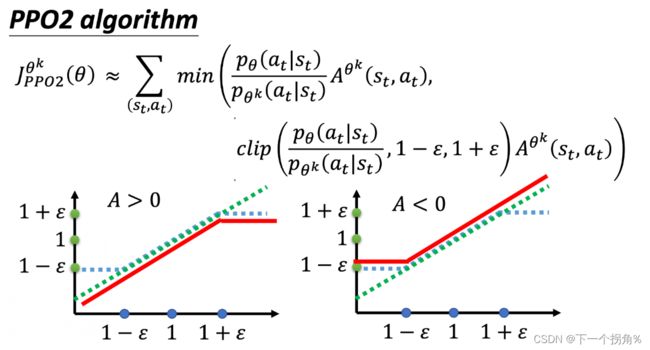
变种2 PPO2--PPO Clip

      提出理由：算 KL 散度很复杂，这个变种 的优化目标函数里没有KL散度。但是仍然要解决 重要性采样的问题  目的：pθ​(at​∣st​) 跟pθk​(at​∣st​)，也就是拿来做示范的模型跟实际上学习的模型，在优化以后不要差距太大。

 

• 第二项前面有个 clip 函数，clip 函数的意思是说，
  • 在括号里面有三项，如果第一项小于第二项的话，那就输出 1-\varepsilon   1−ε 。
  • 第一项如果大于第三项的话，那就输出 1+\varepsilon   1+ε。
• \varepsilon   ε 是一个超参数，可以设成 0.1 或 设 0.2 。

上图的横轴是 pθk​(at​∣st​) / pθ​k(at​∣st​)​，纵轴是 clip 函数的输出。

• 如果pθk​(at​∣st​) / pθk​(at​∣st​)​ 大于 1+ε，输出就是  1+ε。
• 如果小于  1−ε， 它输出就是 1−ε。
• 如果介于  1+ε 跟  1−ε 之间， 就是输入等于输出。

 

代码实践