【鲁棒优化】基于联合聚类和定价的鲁棒功率控制方法（Matlab代码实现）

欢迎来到本博客❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

本文目录如下：

目录

1 概述

2 运行结果

3 参考文献

4 Matlab代码实现

---

1 概述

文献来源：

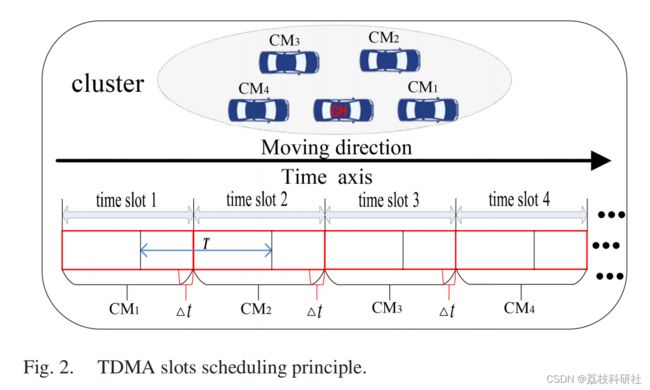
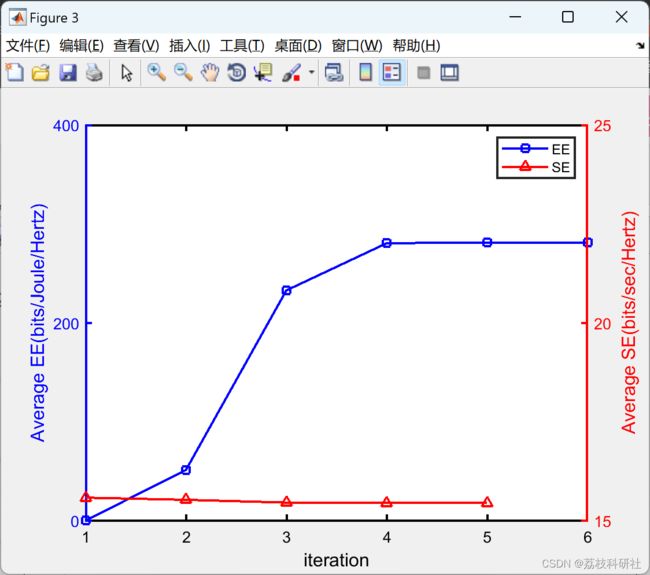
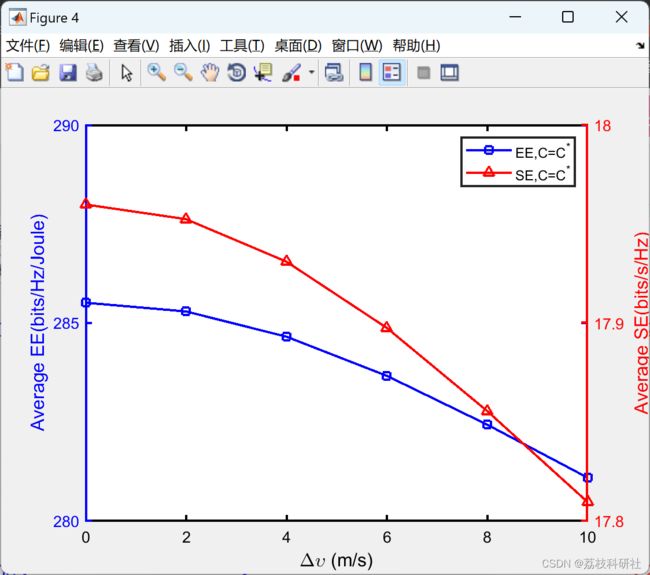
 智能和绿色城市对车载网络的频谱效率（SE）和能源效率（EE）提出了严格的要求。对于当前的车载自组织网络（VANET），车辆的移动性导致快速的拓扑结构变化和高度的信道不确定性。然而，独立研究了用于建立稳定簇的聚类方案和对抗信道波动的鲁棒功率控制（RPC）。本文提出了联合聚类和RPC方案来优化所涉及的VANET的SE和EE。通过相同的固定长度时隙，形成集群头（CH）的同步干扰约束，并为RPC提供条件。由于信道的随机波动，所有通道的同步干扰约束都表述为概率约束。此外，引入了一种基于定价的实用程序，避免了SE和EE之间的单独优化，并且涉及价格对它们之间权衡的影响。由于概率约束是棘手的，并且统一效用是非凸的，因此使用伯恩斯坦近似和逐次凸逼近（SCA）将问题转换为可处理的凸问题。通过对偶分解，提出两种RPC算法来确定固定价格的最优解C，以及最优价格C∗分别。通过数值仿真对高动态系统的算法性能进行了评价，结果表明所提算法是有效的。通过对比进一步验证了聚类方法与所提RPC方案的有效性。

最近，由于车辆通信在提高自动驾驶性能、用户体验和交通效率方面的潜力，引起了极大的关注[1]-[3]。在车载自组织网络（VANET）中，车辆移动性引起的频繁而广泛的拓扑变化需要大量的状态信息交换。此外，希望车辆的数据速率更高，以避免信息丢失并确保交通安全。因此，有必要最大化整个车辆网络的总和率。鉴于频谱资源有限，在车辆通信系统的设计中本能地追求频谱效率（SE）最大化。为了创建智能绿色城市，还需要注重能源效率（EE）最大化和提高出行效率的绿色车辆网络[4]，[5]。因此，EE是系统设计中需要考虑的另一个性能指标。

车载通信有两种主流解决方案，即基于802.11p标准的临时通信和基于后端的通信长期演进（LTE）蜂窝网络[6]，[7]。虽然新鲜的LTE蜂窝网络具有ad-hoc所不具备的这些优势（如覆盖范围广、鲁棒性强），但也存在一些明显的缺陷（如高时延、网络安全防御弱等），成熟的VANET可以完美弥补[8]、[9]。因此，协同通信是车载网络中较好的解决方案。特别是由于车对车（V2V）链路比车对基础设施（V2I）链路具有更复杂的移动环境，本文详细研究了基于VANET的V2V链路。

作为VANET的关键特征，高移动性导致频繁的拓扑变化，不稳定的通信。事实上，集群有助于稳定和可扩展的网络结构和通信[10];鲁棒功率控制（RPC）方案可以在移动信道波动下实现更稳定的性能输出（SE、EE和链路实时中断）[11]。基于这些证据，联合聚类和RPC方案至关重要。

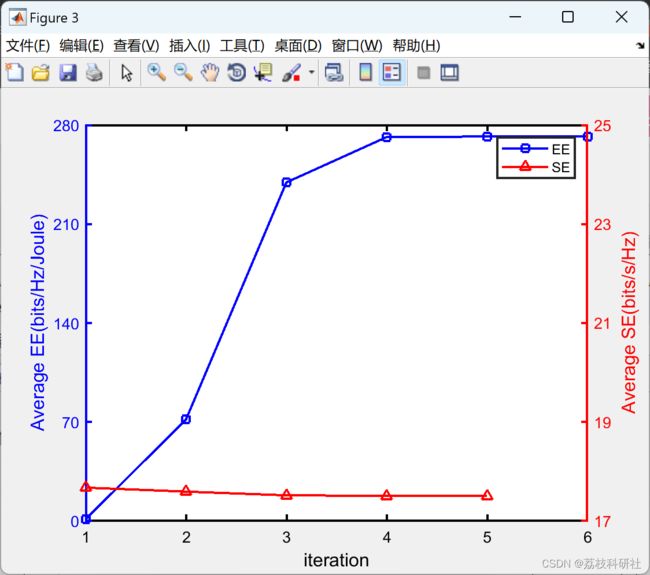
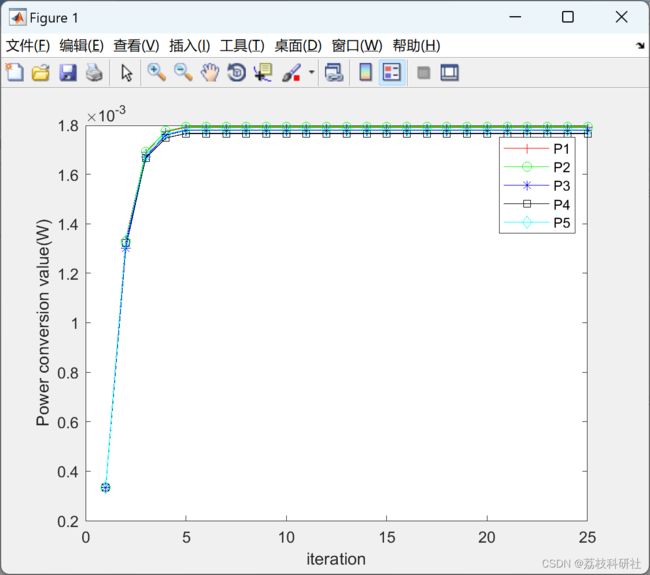
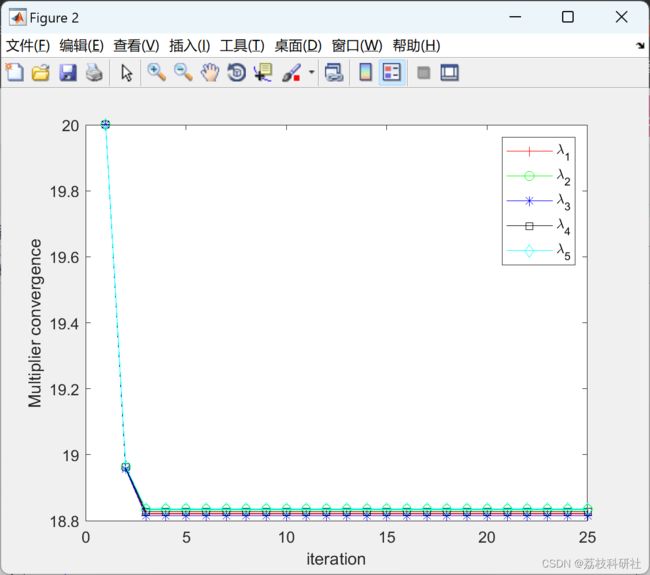
2 运行结果

 

 

 

 

部分代码：

fc=5.9*1e+9;%Carrier frequency
j1=2*pi*fc*T/c*v;%The parameter of zero-order Bessel function
epsi=besselj(0,j1);%Calculate the value of Bessel function
a=(epsi.^2).*h;% CSI feedback part in the fast fading model
d=distance(5);%Relative distance matrix
Shadow=[2.16,0.1,0.1,1.28,1.76;0.1,2.16,0.2,1,2.;1,0.2,2.1,0.1,0.1;1.28,0.1,0.1,2.2,0.21;5.48,2.01,1.06,0.21,2.16];%
%Shadow fading matrix拢禄 The value of element is set as 0.1-10.
%The parameter selection principle is to keep the large-scale fading portion 
%of the interference channel gain as consistent as possible, 
%so that it is easy to make balanced interference management 
%at the same interference threshold.
  theta=3;%Pathloss index
  l=Shadow.*d.^(-theta);%Large scale fading matrix
  G1=l.*a;
  G2=l.*(1-epsi.^2);%Average error channel gain matrix 
  G=G1+G2;
  MU=0.5;%The value of Mu in Bernstein approximation
  SIGMA=0.5;%The value of SIGMA in Bernstein approximation
  alfaj=l.*(1-epsi.^2);%The matrix of alfa
  betaj=l.*(1-epsi.^2);%The matrix of beta
 X=G1+MU*alfaj+betaj;%%The matrix of xi 
      E=0.1;          % Outage probability threshold;
  I=X+SIGMA*sqrt(-2*log(E))*alfaj; 
% --Constructing the interference coefficient matrix of Bernstein approximation--% 
    for i=1:5
      I(i,i)=0;
    end
    
global N
N =25;
arfa=zeros(N,5);%Successive convex approximation coefficient matrix  X
beta=zeros(N,5);%Successive convex approximation coefficient matrix  Y
SINR=zeros(N,5);
Pmax=log(0.5)*ones(N,5);
B=0.01;%Spectrum bandwidth(GHz)拢卢also can be set as 1 or 0.001 which 
%affect the final energy efficiency convergence speed and precision. 
C1=linspace(1,1,5);
GF=linspace(1.5,1.5,5);%Power amplifier coefficient vector.
PC=0.05;%Fixed power consumption in the circuit
 S=zeros(N,5);
 s=zeros(N,5);
Temp=zeros(40,5);%Optimal power storage area for each iteration
 for F=1:10
 C=0.5*F;%Initial fixed price
 Ith=1e-6;%Interference threshold
 Z=1;
 P=zeros(N,5);
P(1,:)=[-8,-8,-8,-8,-8]; 
Lamda=zeros(N,5);
Lamda(1,:)=linspace(10,10,5);
for k=1:N
   for i=1:5
        I1(i)=exp(P(k,:))*G(:,i)+Delta-G(i,i)*exp(P(k,i));
        SINR(k,i)=G(i,i)*exp(P(k,i))/I1(i); 
        arfa(k,i)=SINR(k,i)/(1+SINR(k,i));
        Total_T(k)=B*dot(log(C1+SINR(k,:))/log(2),C1); 

3 参考文献

部分理论来源于网络，如有侵权请联系删除。

4 Matlab代码实现