基于梯度的黑盒迁移对抗攻击(附代码)
1 引言
黑盒迁移攻击是对抗攻击中非常热门的一个研究方向,基于动量梯度的方法又是黑盒迁移攻击的一个主流方向。当前大部分研究主要通过在数据样本的尺寸,分布,规模,时序等方面来丰富梯度的多样性,使得生成的对抗样本在迁移到其它的模型攻击时,能够有更高的攻击成功率。本文会介绍最近几年有代表性的黑盒迁移攻击的论文,这些论文的方法经常会被当成论文比较的baseline。我对论文中涉及到一些数学结论进行补充证明,大部分论文中给出的源码是tensorflow的,我又根据论文的算法流程图用pytorch对论文的核心方法重新编程了一下,代码实例在文末所示。
2 注意力攻击(AOA)
2.1 论文简介
在该论文中作者提出一种注意力攻击 (AoA),注意显著图是深度学习模型共享的语义属性。作者发现当交叉熵损失被注意力损失取代时,AoA方法生成对抗样本的可迁移性会显着提高。除此之外由于AoA方法只改变了损失函数,它可以很容易地与其它对抗样本可迁移性增强技术相结合,从而实现更好的 SOTA 性能。作者应用AoA方法从ImageNet验证集中生成 50000个对抗样本并攻击成功许多神经网络模型,并将数据集命名为DAmageNet,该数据及是第一个通用对抗数据集。

论文链接:https://arxiv.org/abs/2001.06325
数据集链接:http://www.pami.sjtu.edu.cn/Show/56/122
2.2 论文方法
令 h ( x , y ) h(x,y) h(x,y)表示输入 x x x和指定类 y y y的注意力热力图。 h ( x , y o r i ) h(x,y_{\mathrm{ori}}) h(x,yori)是一个与输入 x x x维度一致的张量。
-
抑制损失函数 L s u p p L_{\mathrm{supp}} Lsupp: 其目的是抑制正确类别 h ( x , y o r i ) h(x, y_{\mathrm{ori}}) h(x,yori)的注意力热力图的大小。当正确类的网络注意力降低时,其他类的注意力会增加并最终超过正确的类,从而导致模型寻求获取有关其它类别的信息而不是正确类别的信息,从而做出不正确的预测,具体的损失函数如下所示: L s u p p = ∥ h ( x , y o r i ) ∥ 1 L_{\mathrm{supp}}=\|h(x,y_{\mathrm{ori}})\|_1 Lsupp=∥h(x,yori)∥1其中 ∥ ⋅ ∥ \|\cdot\| ∥⋅∥表示 ℓ 1 \ell_1 ℓ1范数。
-
分散损失函数 L d s t c L_{\mathrm{dstc}} Ldstc: 当注意力从原始感兴趣区域分散时,模型可能会失去预测能力。 在这种情况下,不需要网络关注任何不正确类别的信息,而是引导它关注图像的不相关区域,具体的损失可以表示为以下形式: L d s t c ( x ) = − ∥ h ( x , y o r i ) max ( h ( x , y o r i ) ) − h ( x o r i , y o r i ) max ( h ( x o r i , y o r i ) ) ∥ 1 L_{\mathrm{dstc}}(x)=-\left\|\frac{h(x,y_{\mathrm{ori}})}{\max(h(x,y_{\mathrm{ori}}))}-\frac{h(x_{\mathrm{ori}},y_{\mathrm{ori}})}{\max(h(x_{\mathrm{ori}},y_{\mathrm{ori}}))}\right\|_1 Ldstc(x)=−∥ ∥max(h(x,yori))h(x,yori)−max(h(xori,yori))h(xori,yori)∥ ∥1其中通过进行自归一化以消除注意力大小的影响。
-
边界损失函数 L b d r y L_{\mathrm{bdry}} Lbdry: 其目的是减小 h ( x , y o r i ) h(x, y_{\mathrm{ori}}) h(x,yori)和 h ( x , y s e c ( x ) ) h(x, y_{\mathrm{sec}}(x)) h(x,ysec(x))(即第二大概率的热力图)之间的距离。如果第二类的注意力大小超过正确类的注意力大小,网络将更加关注关于错误预测的信息,具体形式如下所示: L b d r y ( x ) = ∥ h ( x , y o r i ) ∥ 1 − ∥ h ( x , y s e c ( x ) ) ∥ 1 L_{\mathrm{bdry}}(x)=\|h(x,y_{\mathrm{ori}})\|_1 - \|h(x,y_{\mathrm{sec}}(x))\|_1 Lbdry(x)=∥h(x,yori)∥1−∥h(x,ysec(x))∥1不同模型的注意力热力图值差异很大,因此自归一化可以提高对抗样本的可迁移性。 除此之外还可以考虑 h ( x , y o r i ) h(x, y_{\mathrm{ori}}) h(x,yori)和 h ( x , y s e c ( x ) ) h(x, y_{\mathrm{sec}}(x)) h(x,ysec(x))之间的比率,从而得到以下对数边界损失: L l o g ( x ) = log ( ∥ h ( x , y o r i ) ∥ 1 ) − log ( ∥ h ( x , y s e c ( x ) ) ∥ 1 ) L_{\mathrm{log}}(x)=\log(\|h(x,y_{\mathrm{ori}})\|_1)-\log(\|h(x,y_{\mathrm{sec}}(x))\|_1) Llog(x)=log(∥h(x,yori)∥1)−log(∥h(x,ysec(x))∥1)
经实验可知,对数边界损失是迁移攻击效果最好的,因此该损失函数被选为目标函数的中的一项。 此外,注意力攻击可以很容易地与交叉熵损失函数 L C E L_{\mathrm{CE}} LCE相结合,则有AoA损失函数如下所示: L A o A ( x ) = L l o g ( x ) − λ L c e ( x , y o r i ) L_{\mathrm{AoA}}(x)=L_{\mathrm{log}}(x)-\lambda L_{\mathrm{ce}}(x,y_{\mathrm{ori}}) LAoA(x)=Llog(x)−λLce(x,yori)其中 λ \lambda λ是注意力攻击和交叉熵之间的权衡系数。
通过最小化损失函数 L A o A L_{\mathrm{AoA}} LAoA来生成对抗样本,令 x a d v 0 = x o r i x_{\mathrm{adv}}^0=x_{\mathrm{ori}} xadv0=xori,则具体的更新过程如下所示: x a d v k + 1 = c l i p ε ( x a d v k − α g ( x a d v k ) ∥ g ( x a d v k ) ∥ 1 / N ) g ( x ) = ∂ L A o A ( x ) ∂ x \begin{aligned}x_{\mathrm{adv}}^{k+1}&=\mathrm{clip}_{\varepsilon}\left(x_{\mathrm{adv}}^k-\alpha \frac{g(x_{\mathrm{adv}}^k)}{\|g(x^k_{\mathrm{adv}})\ \|_1/N}\right)\\g(x)&=\frac{\partial L_{\mathrm{AoA}}(x)}{\partial x}\end{aligned} xadvk+1g(x)=clipε(xadvk−α∥g(xadvk) ∥1/Ng(xadvk))=∂x∂LAoA(x)其中梯度 g g g进行 ℓ 1 \ell_1 ℓ1范数正则化,其中 N N N表示的是图像像素数量。为了使得对抗扰动不可见,作者通过与原始干净样本的距离来限制对抗攻击的强度。 AoA也可以直接运用到对抗样本的可迁移攻击中,通过输入修改,AoA的可迁移性能得到进一步提高。AoA算法的算法流程图如下所示:

当为有目标攻击时,且攻击目标类别为 y t a r y_{\mathrm{tar}} ytar,则AoA损失函数如下所示: L A o A ( x ) = L l o g ( x ) + λ L c e ( x , y t a r ) = log ( ∥ h ( x , max i ≠ t a r y i ( x ) ) ∥ 1 ) − log ( ∥ h ( x , y t a r ) ∥ 1 ) + λ L c e ( x , y t a r ) \begin{aligned}L_{\mathrm{AoA}}(x)&=L_{\mathrm{log}}(x)+\lambda L_{\mathrm{ce}}(x,y_{\mathrm{tar}})\\&=\log(\|h(x,\max\limits_{i \ne \mathrm{tar}}y_{i}(x))\|_1)-\log(\|h(x,y_{\mathrm{tar}})\|_1)+\lambda L_{\mathrm{ce}}(x,y_{\mathrm{tar}})\end{aligned} LAoA(x)=Llog(x)+λLce(x,ytar)=log(∥h(x,i=tarmaxyi(x))∥1)−log(∥h(x,ytar)∥1)+λLce(x,ytar)
3 线性反向传播(LinBP)
3.1 论文简介
在该论文中,作者重新审视了Goodfellow等人之前提出了一个深度学习模型线性假设,在此基础上作者提出一种增强对抗样本可迁移性的方法线性反向传播 (LinBP),这是一种使用梯度的现成攻击以更线性的方式执行反向传播的方法,该方法在神经网络中正常计算前向传播过程,但在计算反向传播损失时,就好像在前向传播中没有遇到一些非线性激活函数一样。

论文链接:https://arxiv.org/abs/2012.03528
代码链接:https://github.com/qizhangli/linbp-attack
3.2 论文方法
Goodfellow等人曾提出一个假设,即对抗样本的可迁移性其主要原因在于深度学习模型其内在的近似线性特征,类似于在同一数据集上训练的线性模型。如下图所示,每个方格表示CIFAR数据集的一个样本,每个方格里的颜色中白色表示该样本经过模型分类为正确的类别,其它的颜色表示模型分类出错为其它类别。可以发现样本沿着某个方向扰动,分类边界呈现线性特征。

尽管该假设在小数据集模型中的实验里得到了验证,但在大数据集中的大型网络上几乎没有经验证据可以验证它,更不用说在实践中使用该假设。所以,在该论文中,作者首先需要验证大数据集中的大型网络上对抗样本的可迁移性根植于模型的近似线性特征。
给定一个源模型 f : R n → R c f:\mathbb{R}^n\rightarrow \mathbb{R}^c f:Rn→Rc,将输入实例分类输出 c c c类。在该论文中作者比较基于迁移攻击在模型 f f f和更线性的模型 f ′ f^\prime f′(或更非线性的模型 f ′ ′ f^{\prime\prime} f′′)上的成功率。 为简单起见,考虑由一系列权重矩阵 W 1 ∈ R n 0 × n 1 ⋯ , W d ∈ R n d − 1 × n d W_1\in \mathbb{R}^{n_0\times n_1}\cdots,W_d \in \mathbb{R}^{n_{d-1}\times n_d} W1∈Rn0×n1⋯,Wd∈Rnd−1×nd参数化的源模型,其中 n 0 = n n_0 = n n0=n和 n d = c n_d = c nd=c,其输出可以写为 f ( x ) = W d ⊤ σ ( W d − 1 ⊤ ⋯ σ ( W 1 ⊤ x ) ) f({\bf{x}})=W_d^{\top}\sigma(W_{d-1}^{\top}\cdots\sigma(W^{\top}_1{\bf{x}})) f(x)=Wd⊤σ(Wd−1⊤⋯σ(W1⊤x))其中 σ ( ⋅ ) \sigma(\cdot) σ(⋅)是非线性激活函数,一般情况下激活函数会选择ReLU激活函数。由于模型 f f f的非线性仅来自于 σ ( ⋅ ) \sigma(\cdot) σ(⋅)函数,作者通过简单地删除其中一些 σ ( ⋅ ) \sigma(\cdot) σ(⋅)函数来获得所需的 f ′ f^{\prime} f′,从而得到一个与模型 f f f共享相同数量的参数和核心架构的模型。 与使用泰勒展开并在局部获得线性化的某些工作不同,论文作者的方法(称为线性替换,LinS)会导致全局近似。
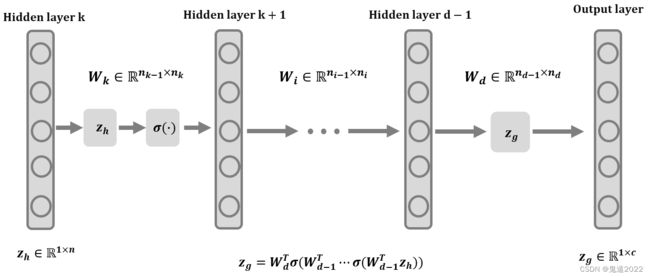
证明: 令 z h = h ( x ) {\bf{z}}_h=h({\bf{x}}) zh=h(x), g g g是分类器 f f f的由第 k k k层到第 d d d层的子网络,激活函数为 R e L U \mathrm{ReLU} ReLU激活函数,即 z g = g ( z h ) = W d ⊤ σ ( W d − 1 ⊤ ⋯ σ ( W k ⊤ z h ) ) = f ( x ) {\bf{z}}_g=g({\bf{z}}_h)=W^{\top}_d \sigma(W_{d-1}^\top\cdots \sigma(W^\top_k {\bf{z}}_h))=f({\bf{x}}) zg=g(zh)=Wd⊤σ(Wd−1⊤⋯σ(Wk⊤zh))=f(x)由矩阵的微分定理可知 d L ( x , y ) = ( ∂ L ( x , y ) ∂ x ) ⊤ d x , d L ( x , y ) = ( ∂ L ( x , y ) ∂ z g ) ⊤ d z g d L({\bf{x}},y)=\left(\frac{\partial L({\bf{x}},y)}{\partial {\bf{x}}}\right)^{\top}d {\bf{x}},\quad d L({\bf{x}},y)=\left(\frac{\partial L({\bf{x}},y)}{\partial {\bf{z}}_g}\right)^{\top}d {\bf{z}}_g dL(x,y)=(∂x∂L(x,y))⊤dx,dL(x,y)=(∂zg∂L(x,y))⊤dzg对 d z g d {\bf{z}}_g dzg求微分可知 d z g = W d ⊤ M d − 1 W d − 1 ⊤ M d − 2 ⋯ W k + 1 ⊤ M k W k ⊤ d z h d {\bf{z}}_g=W^{\top}_dM_{d-1}W^{\top}_{d-1}M_{d-2}\cdots W^{\top}_{k+1}M_{k}W^{\top}_k d{\bf{z}}_h dzg=Wd⊤Md−1Wd−1⊤Md−2⋯Wk+1⊤MkWk⊤dzh对 d z h d {\bf{z}}_h dzh求微分 d z h = ( ∂ z h ∂ x ) ⊤ d ( x ) d{\bf{z}}_h=\left(\frac{\partial {\bf{z}}_h}{\partial {\bf{x}}}\right)^{\top}d({\bf{x}}) dzh=(∂x∂zh)⊤d(x)将以上公式进行整理可得 d L ( x , y ) = ( ∂ L ( x , y ) ∂ z g ) ⊤ W d ⊤ M d − 1 W d − 1 ⊤ M d − 2 ⋯ W k + 1 ⊤ M k W k ⊤ ( ∂ z h ∂ x ) ⊤ d x d L({\bf{x}},y)=\left(\frac{\partial L({\bf{x}},y)}{\partial {\bf{z}}_g}\right)^{\top}W^{\top}_dM_{d-1}W^{\top}_{d-1}M_{d-2}\cdots W^{\top}_{k+1}M_{k}W^{\top}_k\left(\frac{\partial {\bf{z}}_h}{\partial {\bf{x}}}\right)^{\top}d{\bf{x}} dL(x,y)=(∂zg∂L(x,y))⊤Wd⊤Md−1Wd−1⊤Md−2⋯Wk+1⊤MkWk⊤(∂x∂zh)⊤dx进而可推知 ∇ x L ( x , y ) = ∂ L ( x , y ) ∂ x = ∂ z h ∂ x W k M k ⋯ M d − 1 W d ∂ L ( x , y ) ∂ z g ∈ R n × 1 \nabla_{\bf{x}}L({\bf{x}},y)=\frac{\partial L({\bf{x}},y)}{\partial {\bf{x}}}=\frac{\partial {\bf{z}}_h}{\partial {\bf{x}}}W_k M_k \cdots M_{d-1} W_d\frac{\partial L({\bf{x}},y)}{\partial {\bf{z}}_g}\in \mathbb{R}^{n \times 1} ∇xL(x,y)=∂x∂L(x,y)=∂x∂zhWkMk⋯Md−1Wd∂zg∂L(x,y)∈Rn×1当除去激活函数时,此时则有 M k = M k + 1 = ⋯ = M d − 1 M_k=M_{k+1}=\cdots=M_{d-1} Mk=Mk+1=⋯=Md−1,进而则有 ∇ x L ( x , y ) = ∂ L ( x , y ) ∂ x = ∂ z h ∂ x W k ⋯ W d ∂ L ( x , y ) ∂ z g ∈ R n × 1 \nabla_{\bf{x}}L({\bf{x}},y)=\frac{\partial L({\bf{x}},y)}{\partial {\bf{x}}}=\frac{\partial {\bf{z}}_h}{\partial {\bf{x}}}W_k \cdots W_d\frac{\partial L({\bf{x}},y)}{\partial {\bf{z}}_g}\in \mathbb{R}^{n \times 1} ∇xL(x,y)=∂x∂L(x,y)=∂x∂zhWk⋯Wd∂zg∂L(x,y)∈Rn×1论文中采用的是行向量,以上证明是用列向量,所以结论得证。
实验是在 CIFAR-10数据集上使用VGG-19网络和批量归一化得到源模型 f f f进行的。作者移除最后两个 VGG 块中的所有非线性单元以产生初始模型 f ′ f^{\prime} f′,即表示为 f 0 ′ f^{\prime}_0 f0′。它可以写成两个子网的组合,即 f 0 ′ = g ′ ∘ h f^{\prime}_0=g^{\prime} \circ h f0′=g′∘h,所以可知自网络 g 0 ′ g^{\prime}_0 g0′是纯线性的。由于这种简单的“线性化”会导致网络在预测干净样本时的准确性下降,因此作者尝试微调 LinS模型 f ′ f^{\prime} f′。作者评估由模型 f 0 ′ , ⋯ , f m ′ ⋯ f^{\prime}_0,\cdots,f^{\prime}_m\cdots f0′,⋯,fm′⋯在第 0 , ⋯ , m 0,\cdots,m 0,⋯,m轮后生成对抗样本的可迁移性。实验结果如下图所示,这表明LinS方法确实可以提高对抗样本的可迁移性,而且在短期微调的情况下,它大大提高了网络的预测精度。当迭代轮数 m ≥ 1 m \ge 1 m≥1, f m ′ f^{\prime}_m fm′总是有助于生成比模型 f f f更多的可迁移对抗样本,在 f 0 ′ f_0^{\prime} f0′上由I-FGSM生成的对抗样本也实现了不错的可迁移性。当迭代轮数 m = 80 m=80 m=80时,由于过度拟合,进一步的训练会导致可迁移性降低。还能够发现当模型没有ReLU激活函数时,这两个模型都产生了更多可迁移的对抗样本,因此该假设得到了部分验证。
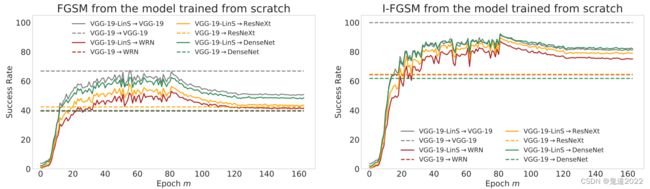
以上实验已经证实,通过直接去除 ReLU层可以获得提高的对抗样本的可转移性,但是删除越多的 ReLU层并不总是意味着更好的性能,因为直接修改架构不可避免地会降低预测精度。如何在线性和准确性之间寻求合理的权衡是一个论文作者接下来要解决的问题。在该论文中作者提出了线性反向传播LinBP方法,其具体的计算公式如下所示: ∇ x L ( x , y ) = d L ( x , y ) d z g W d ⋯ W k d z h d x \nabla_{{\bf{x}}}L({\bf{x}},y)=\frac{d L({\bf{x}},y)}{d {\bf{z}}_g} W_d\cdots W_k \frac{d {\bf{z}}_h}{d {\bf{x}}} ∇xL(x,y)=dzgdL(x,y)Wd⋯Wkdxdzh其中 z h = h ( x ) {\bf{z}}_h=h({\bf{x}}) zh=h(x), g g g是由 f f f的第 k k k层到第 d d d层组成的子网络,则有 z g = g ( z h ) = W d ⊤ σ ( W d − 1 ⊤ ⋯ ( W k ⊤ z h ) ) = f ( x ) {\bf{z}}_g=g({ \bf{z}}_h)=W^{\top}_d\sigma(W^{\top}_{d-1}\cdots(W^{\top}_k{\bf{z}}_h))=f({\bf{x}}) zg=g(zh)=Wd⊤σ(Wd−1⊤⋯(Wk⊤zh))=f(x)LinBP方法不需要微调,因为它前向计算并做出预测,就像训练有素的源模型 f f f一样。如下表可知,与或没有微调的LinS模型相比,LinBP的表现良好,实现了在线性和精度之间进行更合理的权衡。 由于(部分)没有 ReLU,它们都显示出比基线更高的计算效率。
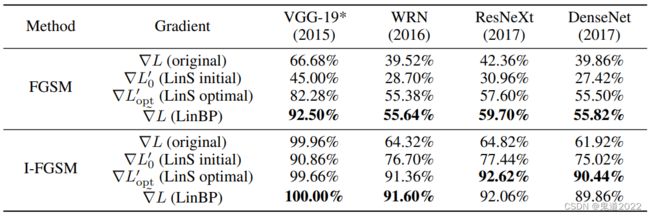
对于残差块 z i + 1 = z i + W i + 1 ⊤ σ ( W i ⊤ z i ) {\bf{z}}_{i+1}={\bf{z}}_i+W^{\top}_{i+1}\sigma(W^{\top}_i{\bf{z}}_i) zi+1=zi+Wi+1⊤σ(Wi⊤zi),标准反向传播计算导数为 d z i + 1 / d z i = 1 + W i M i W i + 1 d{\bf{z}}_{i+1}/d{\bf{z}_i} = 1 + W_iM_iW_{i+1} dzi+1/dzi=1+WiMiWi+1,而“线性化”计算导数为 Ω i = 1 + W i W i + 1 \Omega_i = 1 + W_iW_{i+1} Ωi=1+WiWi+1,其中 M i M_i Mi是一个对角矩阵。作者将梯度进行归一化即在反向传播期间计算 1 + α i W i W i + 1 1 + \alpha_iW_iW_{i+1} 1+αiWiWi+1,其中 α i = ∥ d z i + 1 / d z i − 1 ∥ / ∥ Ω i − 1 ∥ \alpha_i =\| d{\bf{z}}_{i+1}/d{\bf{z}}_i-1\|/\|\Omega_i-1\| αi=∥dzi+1/dzi−1∥/∥Ωi−1∥,标量 α i \alpha_i αi是由梯度自动确定。
4 方差调整动量攻击(VMI-FGSM)
4.1 论文简介
在该论文中,作者提出了一种梯度方差调整的对抗攻击的方法,其目的是增强基于迭代梯度的攻击方法生成对抗样本的可迁移性。在每次迭代进行梯度计算时,不再直接使用当前梯度进行动量累积,而是进一步考虑上一次迭代的梯度方差来调整当前梯度,从而稳定更新方向,避免不良局部最优。

论文链接:https://arxiv.org/abs/2103.15571
代码链接:https://github.com/JHL-HUST/VT
4.2 论文方法
给定目标参数为 θ \theta θ的分类器 f f f和初始干净对抗样本 x ∈ X x\in\mathcal{X} x∈X,其中 x x x是 d d d维, X \mathcal{X} X表示所有的样本。对抗攻击的形式函数如下所示: f ( x ; θ ) ≠ f ( x a d v ; θ ) s . t . ∥ x − x a d v ∥ < ϵ f(x;\theta)\ne f(x^{\mathrm{adv}};\theta)\quad \mathrm{s.t.}\quad \|x-x^{\mathrm{adv}}\|<\epsilon f(x;θ)=f(xadv;θ)s.t.∥x−xadv∥<ϵ对于白盒攻击,可以把对抗攻击看作是一个优化问题,在 x x x的邻域中搜索一个样本,从而最大化目标分类器 f f f的损失函数 J J J: x a d v = arg max x ′ J ( x ′ , y ; θ ) x^{\mathrm{adv}}=\arg\max\limits_{x^{\prime}} J(x^{\prime},y;\theta) xadv=argx′maxJ(x′,y;θ)
定义(梯度方差): 给定具有参数 θ \theta θ和损失函数 J ( x , y ; θ ) J(x, y; \theta) J(x,y;θ)的分类器 f f f,任意图像 x ∈ X x\in\mathcal{X} x∈X和邻域的上限 ϵ ′ \epsilon^\prime ϵ′,梯度方差可以定义为: V ϵ ′ g = E ∥ x ′ − x ∥ p < ϵ ′ [ ∇ x ′ J ( x ′ , y ; θ ) ] − ∇ x J ( x , y ; θ ) V^g_{\epsilon^{\prime}}=\mathbb{E}_{\|x^{\prime}-x\|_p < \epsilon^{\prime}} [\nabla_{x^{\prime}}J(x^\prime,y;\theta)]-\nabla_x J(x,y;\theta) Vϵ′g=E∥x′−x∥p<ϵ′[∇x′J(x′,y;θ)]−∇xJ(x,y;θ)
令 V ( x ) V(x) V(x)来表示 V ϵ ′ g ( x ) V^g_{\epsilon^\prime}(x) Vϵ′g(x),由于输入空间的连续性,不能直接计算 E ∥ x ′ − x ∥ p < ϵ ′ [ ∇ x ′ J ( x ′ , y ; θ ) ] \mathbb{E}_{\|x^\prime-x\|_p<\epsilon^\prime}[\nabla_{x^\prime}J(x^\prime,y;\theta)] E∥x′−x∥p<ϵ′[∇x′J(x′,y;θ)]。 因此,通过在 x x x的邻域采样 N N N个样本来近似其值,计算 V ( x ) V(x) V(x)具体形式如下所示:
V ( x ) = 1 N ∑ i = 1 N ∇ x i J ( x i , y ; θ ) − ∇ x J ( x , y ; θ ) V(x)=\frac{1}{N}\sum\limits_{i=1}^N \nabla_{x^i}J(x^i,y;\theta)-\nabla_x J(x,y;\theta) V(x)=N1i=1∑N∇xiJ(xi,y;θ)−∇xJ(x,y;θ)其中 x i = x + r i x^i=x+r_i xi=x+ri, r i ∼ U [ − ( β ⋅ ϵ ) d , ( β ⋅ ϵ ) d ] r_i\sim U[-(\beta\cdot \epsilon)^d,(\beta\cdot \epsilon)^d] ri∼U[−(β⋅ϵ)d,(β⋅ϵ)d], U [ a d , b d ] U[a^d,b^d] U[ad,bd]表示 d d d维均匀分布。得到梯度方差后,可以用第 ( t − 1 ) (t-1) (t−1)次迭代的梯度方差 V ( x t − 1 a d v ) V(x^{\mathrm{adv}}_{t-1}) V(xt−1adv)调整第 t t t次迭代的 x t a d v x^{\mathrm{adv}}_t xtadv的梯度,以稳定更新方向。论文具体的算法流程图如下所示:

5 梯度加速和尺度不变对抗攻击
5.1 论文简介
在该论文中,作者从将对抗样本生成视为优化过程的角度,提出了两种新的方法来提高对抗样本的可迁移性,即Nesterov迭代快速梯度符号方法(NI-FGSM)和尺度不变攻击方法(SIM)。 NI-FGSM旨在将Nesterov加速梯度适应于迭代攻击中,从而有效地预见并提高对抗样本的可迁移性。SIM方法是基于对深度学习模型的尺度不变特性,利用它来优化输入图像尺度副本上的对抗扰动,以避免对白盒模型的过拟合被攻击并产生更多可转移的对抗样本。 NI-FGSM和SIM可以自然地集成以构建强大的基于梯度的攻击,从而针对防御模型生成更多可转移的对抗样本。

论文链接:https://arxiv.org/abs/1908.06281
代码链接:https://github.com/JHL-HUST/SI-NI-FGSM
5.2 论文方法
NAG是在标准梯度下降法中引入一些轻微的改变,它可以加快训练过程并显着提高收敛性。 NAG可以看作是一种改进的动量方法,其可以表示为:
v t + 1 = μ ⋅ v t + ∇ θ t J ( θ t − α ⋅ μ ⋅ v t ) θ t + 1 = θ t − α ⋅ v t + 1 \begin{aligned}v_{t+1}&=\mu\cdot v_t +\nabla_{\theta_t}J(\theta_t-\alpha\cdot \mu\cdot v_t)\\\theta_{t+1}&=\theta_t-\alpha\cdot v_{t+1}\end{aligned} vt+1θt+1=μ⋅vt+∇θtJ(θt−α⋅μ⋅vt)=θt−α⋅vt+1典型的基于梯度的迭代攻击在每次迭代时贪婪地扰乱梯度符号方向的图像,通常陷入较差的局部最大值,并且比单步攻击表现出弱的可迁移性。但有研究表明在攻击中采用动量可以稳定其更新方向,这有助于摆脱陷入不良的局部最大值并提高可迁移性。与动量相比,除了稳定更新方向之外,NAG的预期更新对先前累积的梯度进行了修正, NAG 的这种前瞻性特性可以帮助更轻松、更快地摆脱不良的局部最大值,从而提高可迁移性。在该论文中作者将 NAG 集成到基于迭代梯度的攻击中,以利用 NAG 的前瞻性属性并构建强大的对抗性攻击,作者将其称为 NI-FGSM。具体来说,在每次迭代中计算梯度之前,会在先前累积梯度的方向上进行一次跳跃。以 g 0 = 0 g_0 = 0 g0=0开始,NI-FGSM的更新过程可以形式化为如下所示: x t n e s = x t a d v + α ⋅ μ ⋅ g t , g t + 1 = μ ⋅ g t + ∇ x J ( x t n e s , y t r u e ) ∥ ∇ x J ( x t n e s , y t r u e ) ∥ 1 x t + 1 a d v = C l i p x ϵ { x a d v + α ⋅ s i g n ( g t + 1 ) } \begin{aligned}x^{\mathrm{nes}}_t&=x^{\mathrm{adv}}_t+\alpha\cdot \mu \cdot g_t,\\g_{t+1}&=\mu\cdot g_t+\frac{\nabla_x J(x^{\mathrm{nes}}_t,y^{\mathrm{true}})}{\|\nabla_x J(x^{\mathrm{nes}}_t,y^{\mathrm{true}})\|_1}\\x^{\mathrm{adv}}_{t+1}&=\mathrm{Clip}_x^\epsilon\left\{x^{\mathrm{adv}}+\alpha\cdot \mathrm{sign}(g_{t+1})\right\}\end{aligned} xtnesgt+1xt+1adv=xtadv+α⋅μ⋅gt,=μ⋅gt+∥∇xJ(xtnes,ytrue)∥1∇xJ(xtnes,ytrue)=Clipxϵ{xadv+α⋅sign(gt+1)}其中 g t g_t gt表示迭代 t t t处的累积梯度, μ \mu μ表示 g t g_t gt的衰减因子。
除了为对抗攻击考虑更好的优化算法外,作者还通过模型增强来提高对抗样本的可迁移性。作者介绍了保损变换和模型增强的正式定义如下所示:
定义(保损变换): 给定一个输入 x x x及其对应的真实标签 y t r u e y^{\mathrm{true}} ytrue和一个分类器 f ( x ) : x ∈ X → y ∈ Y f(x) : x\in\mathcal{X}\rightarrow y \in \mathcal{Y} f(x):x∈X→y∈Y和交叉熵损失 J ( x , y ) J(x, y) J(x,y),如果存在输入变换 T ( ⋅ ) \mathcal{T}(\cdot) T(⋅)对于任意 x ∈ X x \in\mathcal{X} x∈X满足 J ( T ( x ) , y t r u e ) ≈ J ( x , y t r u e ) J(\mathcal{T}(x), y^{\mathrm{true}}) \approx J(x, y^{\mathrm{true}}) J(T(x),ytrue)≈J(x,ytrue) ,则此时 T ( ⋅ ) \mathcal{T}(\cdot) T(⋅)是一个保损变换。
定义(模型增强): 给定一个输入 x x x及其对应的真实标签 y t r u e y^{\mathrm{true}} ytrue和一个分类器 f ( x ) : x ∈ X → y ∈ Y f(x) : x\in\mathcal{X}\rightarrow y \in \mathcal{Y} f(x):x∈X→y∈Y和交叉熵损失 J ( x , y ) J(x, y) J(x,y),如果存在保损变换 T ( ⋅ ) \mathcal{T}(\cdot) T(⋅),使得 f ( x ) = f ( T ( x ) ) f^(x)=f(\mathcal{T}(x)) f(x)=f(T(x)),则此时新的模型为原始模型的模型增强。
在该论文中,作者通过模型增强从原始模型中推导出一组模型,这是一种通过保损变换获得多个模型的简单方法。为了获得保损变换,作者发现深度神经网络除了平移不变性外,还可能具有尺度不变性。具体来说,同一模型上的原始图像和缩放图像的损失值相似。因此,尺度变换可以作为一种模型增强的方法。由上述分析,作者提出了一种尺度不变攻击方法(SIM),它优化了输入图像尺度副本上的对抗扰动: arg max x a d v 1 m ∑ i = 0 J ( S i ( x a d v ) , y t r u e ) s . t . ∥ x a d v − x ∥ ∞ ≤ ϵ \begin{aligned}\arg\max\limits_{x^{\mathrm{adv}}}&\frac{1}{m}\sum\limits_{i=0}J(S_i(x^{\mathrm{adv}}),y^{\mathrm{true}})\\\mathrm{s.t.}\text{ }&\|x^{\mathrm{adv}}-x\|_{\infty}\le \epsilon\end{aligned} argxadvmaxs.t. m1i=0∑J(Si(xadv),ytrue)∥xadv−x∥∞≤ϵ其中 S i ( x ) = x / 2 i S_i(x) = x/2^i Si(x)=x/2i表示输入图像 x x x的比例副本,比例因子为 1 / 2 i 1/2^i 1/2i, m m m表示比例副本的数量。使用SIM攻击,作者可以通过模型增强有效地实现对多个模型的集成攻击,而不是训练一组模型进行攻击。更重要的是,它可以帮助避免对白盒模型的“过拟合”被攻击并生成更具可转移性的对抗样本。
对于生成对抗样本的梯度处理,NI-FGSM引入了更好的优化算法来稳定和纠正每次迭代的更新方向。对于生成对抗样本的集成攻击,SIM 引入了模型增强以从单个模型中派生多个模型进行攻击。因此,NI-FGSM和SIM可以自然地结合起来构建更强的攻击,在论文将其称为 SI-NI-FGSM。 SI-NI-FGSM攻击算法的流程图如下所示:

6 代码实例
以下为本文介绍的相关论文算法的pytorch的代码实现,为方便调用将每个算法都定义成一个函数。尤其需要注意的是,在注意力攻击AoA算法时,会涉及到pytorch对损失函数的二次求导操作,并不能简单的用backward()函数进行实现。
from torchvision import datasets, transforms
from torch.utils.data import DataLoader, Dataset
import torch
import torch.nn as nn
from torch.autograd import Variable
import torch.optim as optim
import torch.nn.functional as F
import os
class CNN(nn.Module):
def __init__(self):
super().__init__()
self.Sq1 = nn.Sequential(
nn.Conv2d(in_channels=1, out_channels=16, kernel_size=5, stride=1, padding=2), # (16, 28, 28) # output: (16, 28, 28)
nn.ReLU(),
nn.MaxPool2d(kernel_size=2), # (16, 14, 14)
)
self.Sq2 = nn.Sequential(
nn.Conv2d(in_channels=16, out_channels=32, kernel_size=5, stride=1, padding=2), # (32, 14, 14)
nn.ReLU(),
nn.MaxPool2d(2), # (32, 7, 7)
)
self.out = nn.Linear(32 * 7 * 7, 10)
def forward(self, x):
x = self.Sq1(x)
x = self.Sq2(x)
x = x.view(x.size(0), -1)
output = self.out(x)
return output
epsilon 和 torch.sign()都会影响扰动大小
def AOA_attack(model, input_x, labels, beta, alpha, epsilon):
input_x.requires_grad = True
# Compute CrossEntropyLoss
outputs = model(input_x)
loss1 = nn.CrossEntropyLoss()(outputs, labels)
grad1 = torch.autograd.grad(outputs[0][labels], input_x, retain_graph = True, create_graph=True) # source map、
one_hot_labels = torch.eye(len(outputs[0]))[labels]
sec_labels = torch.argmax((1-one_hot_labels)*outputs)
grad2 = torch.autograd.grad(outputs[0][sec_labels], input_x, retain_graph = True, create_graph=True) # second map
# Compute Log Loss
loss2 = torch.log(torch.norm(grad1[0],p=1)) - torch.log(torch.norm(grad2[0], p=1))
# AOA loss
loss = loss1 - beta * loss2
delta = torch.autograd.grad(loss, input_x, retain_graph = True)
grad = delta[0]
return input_x + 0.2 * torch.sign(grad)
def AOA_attack(model, input_x, labels, beta, alpha, epsilon):
delta = torch.zeros_like(input_x)
input_x.requires_grad = True
# Compute CrossEntropyLoss
outputs = model(input_x)
loss1 = nn.CrossEntropyLoss()(outputs, labels)
grad1 = torch.autograd.grad(outputs[0][labels], input_x, retain_graph = True, create_graph=True) # source map
one_hot_labels = torch.eye(len(outputs[0]))[labels]
sec_labels = torch.argmax((1-one_hot_labels)*outputs)
grad2 = torch.autograd.grad(outputs[0][sec_labels], input_x, retain_graph = True, create_graph=True) # second map
# Compute Log Loss
loss2 = torch.log(torch.norm(grad1[0],p=1)) - torch.log(torch.norm(grad2[0], p=1))
# AOA loss
loss = loss1 - beta * loss2
delta = torch.autograd.grad(loss, input_x, retain_graph = True)
return input_x + alpha * torch.sign(delta[0])
def FGM_attack(inputs, targets, net, alpha, epsilon, attack_type):
delta = torch.zeros_like(inputs)
delta.requires_grad = True
outputs = net(inputs + delta)
loss = nn.CrossEntropyLoss()(outputs, targets)
loss.backward()
grad = delta.grad.detach()
if type == 'FGSN':
zeta = (torch.norm(inputs, p=0, dim=(2,3), keepdim=True) / torch.norm(inputs, p=2, dim=(2,3), keepdim=True)) * torch.ones(inputs.shape)
delta.data = torch.clamp(delta + alpha * zeta * grad, -epsilon, epsilon)
else:
delta.data = torch.clamp(delta + alpha * torch.sign(grad), -epsilon, epsilon)
delta = delta.detach()
return delta
class SIM_NI(object):
def __init__(self, epsilon, T, mu, m):
self.epsilon = epsilon
self.mu = mu
self.T = T
self.m = m
def attack(self, model, images, labels):
x_adv = images.detach()
g_t = torch.zeros_like(images)
loss_fn = nn.CrossEntropyLoss()
alpha = self.epsilon / self.T
for t in range(self.T):
g = torch.zeros_like(x_adv)
x_nes = x_adv + alpha * self.mu * g_t
for i in range(self.m):
x_temp = (x_nes / (2**i)).detach()
x_temp.requires_grad = True
outputs_temp = model(x_temp)
loss_temp = loss_fn(outputs_temp, labels)
loss_temp.backward()
g += x_temp.grad.detach()
g = g / self.m
g_t = self.mu * g_t + g / torch.norm(g, p=1, dim=(1,2,3), keepdim = True)
x_adv = torch.clamp(x_adv + alpha * torch.sign(g_t), -self.epsilon, self.epsilon).detach()
return x_adv
def SIM_NI_attack(model, images, labels, alpha, mu, m, T):
x_adv = images.detach()
g_t = torch.zeros_like(images)
loss_fn = nn.CrossEntropyLoss()
epsilon = alpha / T
for t in range(T):
g = torch.zeros_like(x_adv)
x_nes = x_adv + alpha * mu * g_t
for i in range(m):
x_temp = (x_nes / (2**i)).detach()
x_temp.requires_grad = True
outputs_temp = model(x_temp)
loss_temp = loss_fn(outputs_temp, labels)
loss_temp.backward()
g += x_temp.grad.detach()
g = g / m
g_t = mu * g_t + g / torch.norm(g, p=1, dim=(1,2,3))
x_adv = torch.clamp(x_adv + alpha * torch.sign(g_t), -0.3, 0.3).detach()
return x_adv
class VMI(object):
def __init__(self, epsilon, beta, N, T, mu):
self.epsilon = epsilon
self.beta = beta
self.mu = mu
self.N = N
self.T = T
def attack(self, model, images, lables):
g = torch.zeros_like(images)
v = torch.zeros_like(images)
x_adv = images.detach()
loss_fn = nn.CrossEntropyLoss()
alpha = self.epsilon / self.T
for i in range(self.T):
x_adv.requires_grad = True
outputs = model(x_adv)
loss = loss_fn(outputs, lables)
loss.backward()
g_prime = x_adv.grad.detach()
g = self.mu * g + (g_prime + v) / torch.norm(g_prime + v, p = 2, dim = (1, 2, 3), keepdim = True)
grad_temp = torch.zeros_like(x_adv)
for k in range(self.N):
x_temp = x_adv.detach() + (torch.randn(x_adv.shape)-0.5) * 2 * self.beta
x_temp.requires_grad = True
output_temp = model(x_temp)
loss_temp = loss_fn(output_temp, lables)
loss_temp.backward()
grad_temp += x_temp.detach()
v = grad_temp / self.N - g_prime
x_adv = torch.clamp(x_adv + alpha * torch.sign(g), 0, 1)
x_adv = x_adv.detach()
return x_adv
def VMI_attack(model, images, lables, iteration, mu, number, epsilon, alpha):
g = torch.zeros_like(images)
v = torch.zeros_like(images)
x_adv = images.detach()
loss_fn = nn.CrossEntropyLoss()
for i in range(iteration):
x_adv.requires_grad = True
outputs = model(x_adv)
loss = loss_fn(outputs, lables)
loss.backward()
g_prime = x_adv.grad.detach()
g = mu * g + (g_prime + v) / torch.unsqueeze(torch.norm(g_prime + v, p=1 , dim=1),1)
grad_temp = torch.zeros_like(x_adv)
for k in range(number):
x_temp = x_adv.detach() + (torch.randn(x_adv.shape)-0.5) * 2 * epsilon
x_temp.requires_grad = True
output_temp = model(x_temp)
loss_temp = loss_fn(output_temp, lables)
loss_temp.backward()
grad_temp += x_temp.detach()
v = grad_temp / number - g_prime
x_adv = x_adv + alpha * torch.sign(g)
x_adv = x_adv.detach()
return x_adv
class AoA(object):
def __init__(self, epsilon, eta, alpha, lambda_, T):
self.epsilon = epsilon
self.eta = eta
self.alpha = alpha
self.lambda_ = lambda_
self.T = T
def attack(self, model, inputs, labels):
x_ori = inputs.detach()
x_adv = inputs.detach()
x_shape = x_ori.shape
N = float(x_shape[0] * x_shape[1] * x_shape[2] * x_shape[3])
k = 0
while torch.sqrt(torch.norm(x_adv-x_ori, p=2)) < self.eta and k < self.T: ## 3.3591
x_adv.requires_grad = True # shape: [1,1,28,28]
outputs = model(x_adv)
loss1 = nn.CrossEntropyLoss()(outputs, labels)
outputs_max, _ = torch.max(outputs, dim=1)
grad1 = torch.autograd.grad(outputs_max, x_adv, grad_outputs = torch.ones_like(outputs_max), retain_graph = True, create_graph=True) # source map
one_hot_labels = torch.eye(len(outputs[0]))[labels]
outputs_sec, _ = torch.max((1-one_hot_labels)*outputs, dim=1)
grad2 = torch.autograd.grad(outputs_sec, x_adv, grad_outputs = torch.ones_like(outputs_sec), retain_graph = True, create_graph=True) # second map
# Compute Log Loss
loss2 = (torch.log(torch.norm(grad1[0], p=1, dim=[1,2,3])) - torch.log(torch.norm(grad2[0], p=1,dim=(1,2,3)))).sum() / x_shape[0]
# AOA loss
loss = loss2 - self.lambda_ * loss1
delta = torch.autograd.grad(loss, x_adv, retain_graph = True)
x_adv = torch.clamp(x_adv - self.alpha * delta[0]/(torch.norm(delta[0], p=1)/N), 0,1).detach()
k = k + 1
return x_adv
def main():
alpha = 0.2
epsilon = 0.5
total = 0
correct1 = 0
correct2 = 0
# model = CNN()
# model.load_state_dict(torch.load('model/model.pt'))
model = torch.load('model_test.pkl')
use_cuda = torch.cuda.is_available()
mnist_train = datasets.MNIST("mnist-data", train=False, download=True, transform=transforms.ToTensor())
train_loader = torch.utils.data.DataLoader(mnist_train, batch_size= 5, shuffle=True)
for batch_idx, (inputs, targets) in enumerate(train_loader):
if use_cuda:
inputs, targets = inputs.cuda(), targets.cuda()
inputs, targets = Variable(inputs), Variable(targets)
total += targets.size(0)
# print(inputs.shape)
outputs = model(inputs)
_, predicted = torch.max(outputs.data, 1)
print('Original:',predicted[1])
# image = torch.unsqueeze(inputs[0],0)
# image = torch.unsqueeze(batch_x[idx],0)
# label = torch.unsqueeze(targets[0],0)
# delta1 = FGM_attack(inputs, targets, model, alpha, epsilon, 'FGNM')
# adv_image1 = torch.clamp(inputs + delta1, 0, 1)
# adv_image1 = VMI_attack(model, inputs, targets, 10, 0.9, 5, 0.2, 0.2) # successful
# adv_image1 = SIM_NI_attack(model, inputs, targets, 0.1, 0.9, 5, 10) #successful
# adv_image1 = AOA_attack(model, image, label, 0.1, 0.2, 0.3)
# adv_type = AoA(epsilon = 0.5, eta = 0.8, alpha = 0.3, lambda_ = 0.8, T = 10)
# adv_image1 = adv_type.attack(model, inputs, targets)
adv_type = VMI(epsilon = 10, beta = 0.3, N = 10, T = 10, mu = 0.9) # epsilon太小了
adv_image1 = adv_type.attack(model, inputs, targets)
# adv_type = SIM_NI(epsilon=0.5, T=10, mu=0.9, m=4)
# adv_image1 = adv_type.attack(model, inputs, targets)
outputs1 = model(adv_image1)
_, predicted1 = torch.max(outputs1.data, 1)
correct1 += predicted1.eq(targets.data).cpu().sum().item()
# print('The FGNM accuracy:', correct1, total, correct1/total)
print('AOA_attack:', predicted1[1])
delta2 = FGM_attack(inputs, targets, model, alpha, epsilon, 'FGSM')
adv_images2 = torch.clamp(inputs + delta2, 0, 1)
outputs2 = model(adv_images2)
_, predicted2 = torch.max(outputs2.data, 1)
correct2 += predicted2.eq(targets.data).cpu().sum().item()
# print('The FGSM accuracy:', correct2, total, correct2/total)
print('FGSM:', predicted2[1])
# print('The FGNM accuracy:', correct1)
# print('The FGSM accuracy:', correct2)
if __name__ == '__main__':
main()