CASREL 总结

框架的核心 (The core of the framework)

框架的核心是崭新的视角，我们可以将关系建模为将主体映射到对象的函数，而不是将关系视为实体对的分离标签

将学习关系分类器从 $f(s,o)$ $\to$ $r$ 转换至特定与关系的标记器 $f_r(s)$ $\to o$ 对每一个句子 都在特定关系下识别给定主体的可能对象，或者不返回任何对象，表明没有给定主体和关系的三元组。

三元组划分为两个过程：

• 首先，我们在句子中确定所有可能的主体，
• 然后，对于每个主体，我们应用特定于关系的标记器来同时识别所有可能的关系和相应的对象

CASREL（一个端到端的级联二进制标记框架）由基于 BERT 的编码器模块组成，主体标记模块，特定于关系的对象标记模块。实证实验证明，

• 即使未对 BERT 编码器进行预训练，所提出的框架在很大程度上也优于最新方法。
• 在采用预先训练过的 Bert 编码器之后，该框架获得了进一步的性能提升。

相关的工作 (Related Work)

从非结构化的自然语言文本中提取关系三元组是信息提取 (即) 中一项经过充分研究的任务。

这也是构建大规模知识图( KG ) 重要步骤，例如 DBpedia，Freebase and Knowledge Vault

CasRel 框架 (The CasRel Frame)

关系三重提取的目的是确定句子中所有可能的 （主语，关系，宾语）三元组，其中一些三元组可能与主体或客体共享相同的实体。

为此这里直接对三元组进行建模，并在三重级别上设计一个训练目标。而之前的训练目标为实体和关系分别定义的的，而没有在三重级别上明确地对其集成进行建模。

正式的，我们从训练集 $D$ 中给定注释的句子 $x_i$，并从中给出一组潜在的重叠三元组 $T_j=\{(s,r,o)\}$， 旨在最大化训练集 $D$ 的数据可能性：

$$\begin{array}{rl}& \prod ^{|D|}j=1\left[\prod (s,r,o)\in T_{j}p((s,r,o)\mid x_j)\right]\\ =& \prod ^{|D|}j=1\left[\prod s\in T_{j}p(s|x_j)\prod _{(r,o)\in T_j|s}p((r,o)|s,x_j)\right]\\ =& \prod ^{|D|}j=1\left[\prod s\in T_{j}p(s|x_j)\prod _{r\in T_j\mid s}{p}_r(o|s,x_j)\prod _{r\in R\setminus T_j\mid s}{p}_r(o_{\varnothing }|s,x_j)\right]\end{array}$$

$s\in T_j$表示在 $T_j$ 中的三元组中出现的类型 $s$，

$T_j|s$ 表示实体 $s$ 类型主导的在 $T_j$ 的三元组.

该模型激发了一种用于三重提取的新颖的标记方案，这里学习了一个客体标记 $p(s|x_j)$，该类型标记了句子中的类型主体，对于每个关系 $r$，这里学习了一个客体标记器 $p_r(o|s,x_j)$，客体识别给定类型的特定关系客体，

通过这种方式，我们可以将每个关系建模为映射到主体到客体的函数，而不是对(主体，客体)对的关系进行分类。

• 首先运行主体标记器，以查找句子中的所有可能主体；
• 然后对于找到的每个主体，应用特定与关系的客体标记器以查找所有相关关系的响应客体。

上述为常规框架中的关键组件，即**主体标记器和特定与关系的客体标记器，可以通过多种方式实例化。**下面是在深层双向变压器 Bert 的顶部作为二元实例化它们。

BERT 编码器

编码器模块从句子 ${\mathrm{X}}_{\mathrm{j}}$ 中提取特征信息 $x_j$，它将输入到后续的标记模块中。这里采用预训练的**BERT模型**来对上下文信息进行编码。这是种基于多层双向变压器的语言表示模型。

请注意，在 CASREL 中，输入的是单个文本句子，而不是句子对，因此在等式中未考虑 BERT 论文中所述的分割嵌入（Token Embedding、Segment Embedding、Position Embedding）。

级联解码器 (Cascade Decoder)

下面描述的是对先前公式的新型 Cascade 二进制标记方案的实例化。

基本思想是通过两个级联步骤提取，首先，我们从输入句子中检测到主体，然后对于每个候选主体，检查所有可能的关系，以查看关系是否可以将句子中的客体与该主体关联。

对应于这两个步骤：

级联解码器由两个模块组成，

1. 一个主体标记器
2. 以及一组特定与关系的客体标记器

Subject Tagger (主体标记器)

低级标记模块旨在通过直接对由N层bert编码器产生的 ${\mathrm{h}}_{\mathrm{N}}$编码向量解码，来识别输入句子中所有可能的主体。

更确切的说，它采用两个相同的二进制分类器，通过为每个 token 分配一个二进制标签（0/1）来分别检测客体的起始和结束位置，该标记指示当前 token 是否对应于客体的起点或终点位置

每个 token 上的 subject tagger 详细操作如下：

$$\begin{array}{r}{p}_i^{start\_s}=\sigma ({\mathrm{W}}_{start}{\mathrm{x}}_i+{\mathrm{b}}_{start})\\ p_i^{end\_s}=\sigma ({\mathrm{W}}_{end}{\mathrm{x}}_i+{\mathrm{b}}_{end})\end{array}$$

其中 $p_i^{start\_s}$ 和 $p_i^{end\_s}$ 在输入序列中识别第 $i$ 个 token 牌的概率。

如果概率超过某个阈值，则将使用标签 1 分配相应的 token ，否则将分配标签给标签 0

${\mathrm{x}}_i$ 是输入序列中第 $i$ 个 token 的编码表示。

${\mathrm{x}}_i={\mathrm{h}}_N[i]$，其中 ${\mathrm{W}}_{(\cdot )}$代表可训练的权重， ${\mathrm{b}}_{(\cdot )}$ 是偏差， $\sigma$ 是 sigmoid 激活函数

主体标注器优化以下似然函数以识别给定句子表示 x 的主题 s 的跨度（最大值减去最小值）：

$$\begin{array}{c}\begin{array}{rl}& p_{\theta }(s|\mathrm{x})\\ =& \prod _{t\in \{start\_s,end\_s\}}\prod _{i=1}^L(p_i^t{)}^{I\{y_i^t=1\}}(1-p_i^t{)}^{I\{y_i^t=0\}}\end{array}\end{array}$$

其中 $L$ 是句子的长度，如果 z 为 true $\mathrm{I}\{z\}=1$ ，否则为 0，

$y_i^{start\_s}$ 是 $\mathrm{x}$ 中第 $i$ 个 token 的主体起始位置的二进制 $i$ 标签，而 $y_i^{end\_s}$ 是指主体结束位置

参数 $\theta =\{{\mathrm{W}}_{\mathrm{start}},{\mathrm{b}}_{\mathrm{start}},{\mathrm{W}}_{\mathrm{end}},{\mathrm{b}}_{\mathrm{end}}\}$

上图例，表现出，有三个候选头实体被检测到在低水平的情况下(上述的低级标记模块)，虽然高水平的 0/1 标签是第一个主体的；

当 $k=1$时，迭代状态的快照如上所示；

对于随后的迭代（ $k$=2,3），高水平的结果将改变，反映了检测到的不同三元组。

例如，当 $k$ = 2 时，高级橙色（绿色）块将分别更改为0（1），反映由第二个候选主体Washington 的三重关系，(Washington，Capital，United States Of America)。

对多个客体检测，采用了最近的起始段对匹配原理，根据起始位置和终点标记器的结果来确定任何主体的跨度。例如：到第一个开始的 token “Jackie” 的最近的末端 token 为”Brown”,因此第一个主体跨度的检测结果为 ”Jackie R. Brown”。

但是值得注意的是，要匹配给定开始 token 的结束 token ，这里我们未考虑其位置在给定 token 位置之前的 token。（也就是没考虑从客体到主题这种情况，都是从选定主体的后方进行一系列的操作）。如果给定句子中任何实体跨度有自然连续性，且正确检测到起始位置和结束位置，则此类匹配策略能够维持任何实体跨度的完整性。

Relation-specific Object Taggers (特定与关系的客体标记器)

高级别的标记模块同时识别客体以及相对于较低级别获得的客体的关系。上图所示，它有一组特定于关系的客体标记器组成，其结构与低级模块中的主体标记器相同，用于所有可能的关系。。

与直接解码编码的矢量 ${\mathrm{h}}_N$ 的主体标记器不同，特定与关系的客体标记也考虑了主体特征，每个 token 上特定与关客体的标记器的详细操作如下：

$$\begin{array}{r}{p}_i^{star{t}_o}=\sigma ({\mathrm{W}}_{start}^r({\mathrm{x}}_i+{\mathrm{v}}_{sub}^k)+{\mathrm{b}}_{start}^r)\\ p_i^{en{d}_o}=\sigma ({\mathrm{W}}_{end}^r({\mathrm{x}}_i+{\mathrm{v}}_{sub}^k)+{\mathrm{b}}_{end}^r)\end{array}$$

其中 $p_i^{start\_o}$ 和 $p_i^{end\_o}$ 表示分别在输入序列中标识第 $i$ 个 token 作为客体的开始和结束位置的概率，而 ${\mathrm{v}}_{sub}^k$ 表示在低级模块中检测到的第 $k$ 个主体的编码表示矢量。

对于每个主体，迭代地对其应用相同的解码过程

注意：该主体通常由多个 token 组成，所以在等式中添加 ${\mathrm{x}}_i$ 和 ${\mathrm{v}}_k$。

我们需要使两个向量的维保持一致，为此，将第 $k$ 个主题的起始和终点之间的平均向量表示为 ${\mathrm{v}}_{sub}^k$。

关系的客体标记器优化以下似然函数，以识别客体的跨度 $o$ 给定句子表示 $\mathrm{x}$ 的主体。

$$\begin{array}{c}\begin{array}{rl}& p_{{\varphi }_r}(o|s,\mathrm{x})\\ =& \prod _{t\in \{start\_o,end\_o\}}\prod _{i=1}^L(p_i^t{)}^{I\{y_i^t=1\}}(1-p_i^t{)}^{I\{y_i^t=0\}}\end{array}\end{array}$$

其中 $y_i^{start\_o}$ 是 $\mathrm{x}$ 中第 $i$ 个 token中客体的开始位置， $y_i^{end\_o}$ 是 $\mathrm{x}$ 中第 $i$ 个 token中客体的结束位置，对于 “null” 客体 $o_{\varnothing }$，对所有的 $i$ 标签 $y_i^{start\_o_{\varnothing }}$= $y_i^{end\_o_{\varnothing }}$ = 0。参数 ${\varphi }_r=\{W_{start}^r,b_{start}^r,W_{end}^r,b_{end}^r\}$。

注意：在高级标记模块中，该关系也由客体标记的输出决定。

例如：

1. 检测到的主体 “Jackie R. Brown” 和 候选客体 “Washington”之间不存在关系 “Work_in”。因此，用于 “Work_in” 的关系的客体标记器将无法识别 “Washington“ 的范围，即起始位置和终点的输出为零。
2. 相反的，“出生地” 之间的关系保持在 “Jackie R. Brown” 和 “Washington”之间，因此，相应的客体标记器输出候选客体 “Washington” 的跨度。
3. 在这种情况下，高级模块能够同时识别与低级模块中检测到的主体的关系和对象。

Data Log-likelihood Objective

作者将前文提到的 formulation 中的公式(3)取对数，得到对数似然函数目标 $j(\theta )$如下：

$$\begin{gathered} \begin{array}{r}\sum _{j=1}^{|D|}\left[\sum _{s\in T_j}\log p_{\theta }(s|{\mathrm{x}}_j)+\sum _{s\in T_j|s}\log p_{{\varphi }_r}(o|s,{\mathrm{x}}_j) \\ +\sum _{r\in R\setminus T_j|s}\log p_{{\varphi }_r}(o_{\varnothing }|s,{\mathrm{x}}_j)\right]\end{array} \end{gathered}$$

参数 $\theta =\{\theta ,\{{\varnothing }_r{\}}_{r\in R}\}$，在 shuffle 的 mini-batches 的基础上使用 Adam 随机梯度下降最大化 $J(\theta )$ 来训练模型

实验 (Experiments)

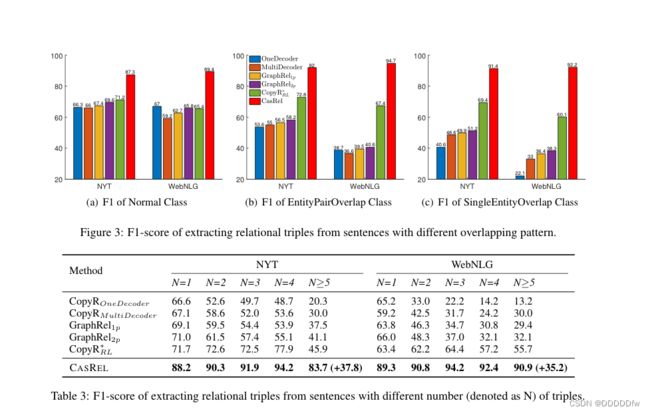
这些都是一些训练结果的表述

论文链接地址：https://arxiv.org/pdf/1909.03227v4.pdf