C语言经典案例详解|九九乘法表 素数 最大公约数 猜数字游戏
目录
1.九九乘法表:
2.素数
3.最大公约数
4.猜数字游戏
生成随机数
随机数的本质
重新播种
生成一定范围内的随机数
连续生成随机数
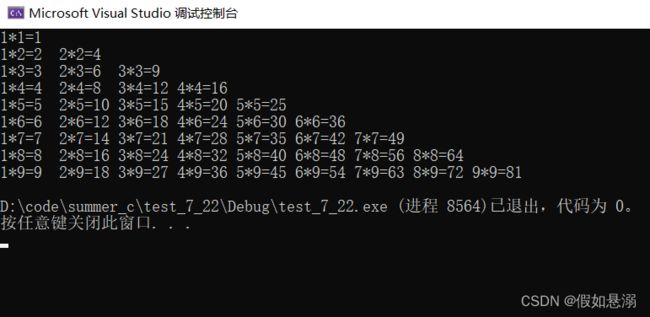
1.九九乘法表:
学习完C语言的循环语句后,我们会遇到很多九九乘法表的问题,在这我们进行一系列的分析。
九九乘法表的格式是x*y=z的格式。
接下来,我们要做的是利用循环结构,通过i控制行数,行数i确定后j控制列数从1到i,最后,要对乘法表没有对齐进行优化处理。
代码如下:
#include
int main()
{
int i, j;
for (i = 1; i <= 9; i++)
{
for (j = 1; j <= i; j++)
{
//printf("%d*%d=%d", j, i, i * j);无法对齐,改进:
printf("%d*%d=%-3d", j, i, i * j);
//%3d,控制打印整数时占3格,位数不够左边补空格右边对齐,%-3d左对齐
}
printf("\n");
}
return 0;
} 变式:实现一个函数,打印乘法口诀表,口诀表的行数和列数自己指定
如:输入9,输出9*9口诀表,输出12,输出12*12的乘法口诀表。
#include
int main()
{
int i, j;
int line = 0;
scanf("%d", &line);
for (i = 1; i <= line; i++)
{
for (j = 1; j <= i; j++)
{
if (i < 10)
{
printf("%d*%d=%-5d", j, i, i * j);
}
else
{
printf("%d*%d=%-4d", j, i, i * j);
}
}
printf("\n");
}
return 0;
} 如果行数大于10行可能会对不齐,采用if else可以保证尽量更整齐一些。
2.素数
方法一:暴力循环
int isprime(int a)
{
int i = 0;
for (i = 2; i < a; i++)
{
if (a % i == 0)
{
return 0;
}
}
return 1;
}
//改进:把a改成根号a,以为不被i整除,因为a如果有两个整数因数那么一定在根号a两边各一个。方法二:筛选法
具体做法是:先把N个自然数用数组存起来,默认全为素数然后一个个去除不是素数的把值改为0。先划去一,2是质数留下来把,把2的倍数都划去。2后面第一个没划去的数是3,把3留下,再把3后面所有3倍数的数都划去。3后面第一个没划去的数是5,把5留下,再把5后面所有5倍数的数都划去。直到把小于N的全部合数都筛掉,留下的就是不超过N的全部质数。得到一张全是素数的表,可以直接查询要求的素数是否是素数
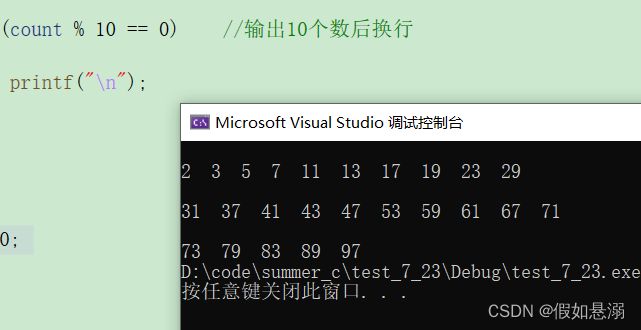
1-100为例:
#include
int main()
{
int i = 0;
int arr[101] = { 0 };
//初始化数组为0 1 2 3 4 5 6 7 8 9 ……100
for (i = 0; i <= 100; i++)
{
arr[i] = i;
}
//开始筛选
arr[1] = 0;//先把一设为非素数
int index=2;//记录素数的下标也就是数字本身,从2开始
while (index <= 100)
{
i = 2;
//把值为index的数的倍数全变成0,i表示2倍,3倍,4倍……
while (index * i <= 100)
{
arr[index * i] = 0;
i++;
}
//向前进找到最近的素数下标
do {
index++;
} while (arr[index] == 0);
}
//输出
int count = 0; //计数器
for (i = 1; i <= 100; i++)
{
if (arr[i] != 0)
{
printf("%d ", arr[i]);
count++;
}
if (count % 10 == 0) //输出10个数后换行
{
printf("\n");
}
}
return 0;
} 3.最大公约数
1.暴力遍历法
int gcd(int n1,int n2)
{
int i = 0;
int n = (n1 > n2 ? n2 : n1);
for (i = n; i >=1 ; i-- )
{
if (n1 % i == 0 && n2 % i == 0)
{
return i;
}
}
return 1;
}2.辗转相除法(递归或循环)
//循环
int gcd(int n1, int n2)
{
int num = 0;
while ((num = n1 % n2) != 0)
{
n1 = n2;
n2 = num;
}
return n2;
}
//递归
int gcd(int n1, int n2)
{
if (n1 % n2 == 0)
{
return n2;
}
else
{
return gcd(n2, n1 % n2);
}
}不用管n1和n2谁更大,只要两个整除时,返回n2就可以。
4.猜数字游戏
生成随机数
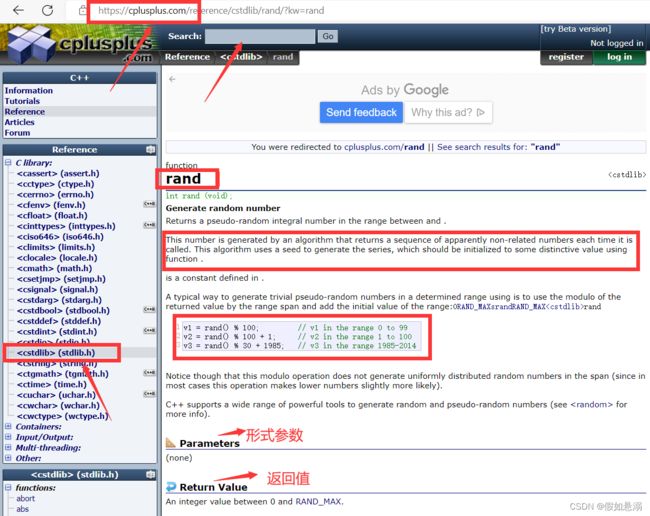
rand函数:(cplusplus.com - The C++ Resources Network在这个网址查看专门定义和功能)
int rand (void);功能生成随机数0-RAND_MAX,此数字由一种算法生成,该算法每次调用时都会返回一系列明显不相关的数字。
随机数的本质
多次运行上面的代码,结果每次产生的随机数都一样,为什么随机数不随机?
实际上,rand() 函数产生的随机数是伪随机数,是根据一个数值按照某个公式推算出来的,这个数值我们称之为“种子”。该算法使用种子来生成序列,应使用函数将其初始化为某个独特的值。种子和随机数之间的关系是一种正态分布,如下图所示:
种子在每次启动计算机时是随机的,但是一旦计算机启动以后它就不再变化了;也就是说,每次启动计算机以后,种子就是定值了,所以根据公式推算出来的结果(生成的随机数)就是固定的。就意味着我们要种不同的种子。
重新播种
我们可以通过 srand() 函数来重新“播种”,种子会发生改变。srand() 的用法为:
void srand (unsigned int seed);
它需要一个 unsigned int 类型的参数。在实际开发中,我们可以用时间作为参数,只要每次播种的时间不同,那么生成的种子就不同,最终的随机数也就不同。
我们一般使用time() 函数得到当前的时间
srand((unsigned)time(NULL));
注:time()函数需要引用#include
生成一定范围内的随机数
我们往往需要一定范围内的随机数,如何产生呢?我们可以利用取模的方法:
int a = rand() % 10; //产生0~9的随机数,一个数模10得到余数最大为9
int a = rand() % 61 + 13; //产生0~60的随机数
int a = rand() % 61 + 13; //产生13~73的随机数
要产生n-m的数,可以rand()%(m-n)+n
注:此模运算不会在跨度中生成均匀分布的随机数(因为在大多数情况下,此操作使较小的数字的可能性略高)。
//完整代码
#include
#include
#include
int main(){
int a;
srand((unsigned)time(NULL));
a = rand() % 51 + 13;
printf("%d\n",a);
return 0;
} 连续生成随机数
如果需要产生一组连续随机数,如何生成呢?
//如果:
for (i = 0; i < 10; i++) {
srand((unsigned)time(NULL));
a = rand();
printf("%d ", a);
}
return 0;
}
//运行后会发现也不随机
为什么生成的随机数都一样呢?
这是因为,for循环运行速度非常快,在一秒之内就完成了,time() 函数得到的时间精确到秒,所以所以每次循环得到的时间都是一样的,种子就是一样的,随机数也就一样了。所以我们经常地在主函数前面就使用srand,而不是反复使用srand。在猜数字游资里也是这样。
//猜数字游戏
#include
#include
#include
#include
void menu()
{
printf("-------------welcom!-------------\n");
printf("---------请输入您的选择:--------\n");
printf("----1.开始游戏------2.exit-------\n");
}
void game()
{
int guessnum = rand() % 100 + 1;
int tmp = 0;
printf("游戏开始请输入您猜的数字:\n");
while (1)
{
scanf("%d", &tmp);
if (tmp > guessnum)
{
printf("您猜大了,请重新猜:\n");
}
else if (tmp < guessnum)
{
printf("您猜小了,请重新猜:\n");
}
else
{
printf("恭喜您,猜对了!\n");
break;
}
}
}
int main()
{
int flag = -1;
srand((unsigned)time(NULL));
menu();
while (flag != 2)
{
scanf("%d", &flag);
if (1 == flag)
{
system("cls");
game();
Sleep(100);
menu();
}
else if (2 == flag)
{
printf("成功退出游戏!");
}
else
{
printf("您输入的数字有误,请重新输入!\n");
}
}
}