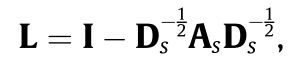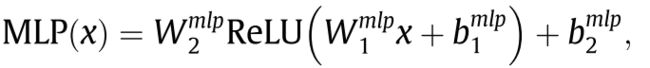Meta Graph Transformer: A Novel Framework for Spatial–Temporal Traffic Prediction
Meta Graph Transformer: A Novel Framework for Spatial–Temporal Traffic Prediction
作者:Xue Ye, Shen Fang, Fang Sun, Chunxia Zhang, Shiming Xiang(中国科学院)下载链接代码链接:Code
2021.12.12 accepted
Abstract
- 目前traffic state prediction任务中挑战是如何同时利用时空异质性建模交通的复杂动态行为。( 时空异质性: 不同时间和不同空间的交通行为均不相同。)
- 本文提出了一个 M G T ( m e t a − g r a p h t r a n s f o r m e r ) MGT(meta-graph transformer) MGT(meta−graphtransformer)解决了该问题。MGT是transformer的variant。Encoder部分将历史traffic data编码成intermediate representations,解码器采用auto-regressively方式预测future traffic state。MGT主要包含三个blocks,TSA(temporal self-attention),SSA(spatial self-attention),TEDA(temporal encoder-decoder attention)(都是multi-head 结构)。
- Encoder和Decoder都包含TSA和SSA,来捕获时间和空间相关性。TEDA只在Decoder部分,让decoder部分的每一个position都试图去参与输入序列的所有position。(输入 X 1 , X 2 , . . . , X t X_{1},X_{2},...,X_{t} X1,X2,...,Xt,预测 X t + 1 X_{t+1} Xt+1,TEDA能让 X t + 1 X_{t+1} Xt+1参与 X 1 , . . . , t 的 每 个 位 置 X_{1,...,t}的每个位置 X1,...,t的每个位置)
- 通过利用多图,SSA可以进行具有各种归纳偏差的稀疏空间注意的计算。为了促进模型对时间和空间条件的感知,STE(spatial - temporal Embeddings)需要从外部属性中学习,这些外部属性由时间属性(相对顺序、绝对时间)和空间属性(如拉普拉斯特征映射)组成。学习得到的Embedding通过meta-learning被所有Attention层利用,即可赋予attention层时空异质性感知(Spatial-temporal-hererogeneity-aware, STHA)属性。
1 Introduction
时空异质性
时空异质性可以增强时序建模的能力。如下图所示,给定两个时间段 ( e , b ) (e,b) (e,b), ( f , d ) (f,d) (f,d),时间跨度相同(1小时),数值相同。因为 ( e , b ) (e,b) (e,b)是高峰时段,其的关联性肯定比 ( f , d ) (f,d) (f,d)强。时空同质性的方法就没有考虑这一点。

一些研究STSGCN,GMAN,Adapative GCRN,ASTGNN考虑了时空异质性。但他们要么在序列level上考虑异质性,要么通过时空嵌入和输入(特征)的直接串联或求和引入异质性。前者不能整合全局时间信息,后者混淆了两种不同类型数据之间的关系。
本文提出了一种MGT框架来解决交通预测问题。MGT充分利用了时间和空间两个维度上的注意机制。因此,它具有所有Attention的优点,如动态相关性、高效的长期建模和易于并行化。此外,我们设计了一个meta-learning过程(因此命名为Meta Graph Transformer),将从外部时间和空间属性中学习到的元知识整合到注意层中,从而使我们的模型能够执行时空异质性感知(STHA)注意。更重要的是,将多个图表整合到我们的空间注意层中,以便考虑各种类型的空间相关性。模型的贡献总结如下:
- 提出了一种将元学习整合到注意机制中的框架,以捕获交通预测任务中的时空异质性。
- 将外部的时空属性融合为时空嵌入(spatial - temporal Embeddings, STEs),在STEs的引导下设计了三种注意层,分别在时空维度上进行STHA操作。
- 为了更好地捕捉不同类型的空间依赖性,创建了空间注意力的多图版。
- 在三个交通数据集上进行了大量的实验,以评估提出的模型。结果表明,我们的模型明显优于目前最先进的方法。(SOTA)
2 Related work
后面有空再补。
3 Preliminaries
3.1 Problem Formulation
- traffic network: g = ( V , E , A ) , V = { V 1 , V 2 , . . . , V N } g=(V,E,A),V=\{V_1,V_2,...,V_N\} g=(V,E,A),V={V1,V2,...,VN}表示 nodes ,交通系统中的点(传感器,路段,交叉路口或地铁站) E E E是边, A A A是adjacency 矩阵。
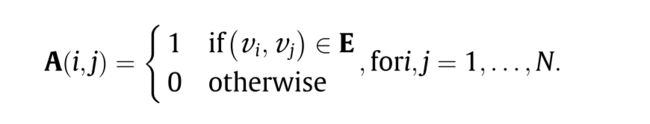
- traffic state:node i i i在time t t t 的traffic state定义为 X t i ∈ R c X_t^i \in{R^c} Xti∈Rc(C是特征数量) X t = [ X t 1 , X t 2 , . . . , X t N ] ∈ R N × C X_t=[X_t^1,X_t^2,...,X_t^N] \in R^{N\times C} Xt=[Xt1,Xt2,...,XtN]∈RN×C 表示所有节点在time t的traffic state.
- temporal attributes:每个时间t都附加了几个时间属性,比如天、星期和知否休息日。假设有 M M M个可用的时间属性,time t t t的第 m m m个属性被定义为 T t m ∈ { 1 , 2 , . . . , N m } T_t^m \in \{1,2,...,N_m\} Ttm∈{1,2,...,Nm}, N m N_m Nm是可能状态的数量(one-hot).
- multiple graph: 基于特定的领域知识(距离、相似度等),可以构造多个图来解释节点之间的不同关系(详见4.3.1节)。这些图被定义为 { g b = ( V , E b , W b ) } b = 1 B \{g_b = (V,E_b,W_b)\}_{b=1}^B {gb=(V,Eb,Wb)}b=1B,B是图的数量,所有图都共享nodes V V V.
- proof
输入:过去 P time intervals X = [ X t − p , X t − p + 1 , . . . , X t − 1 ] ∈ R P × N × C X=[X_{t-p},X_{t-p+1},...,X_{t-1}] \in R^{P \times N \times C} X=[Xt−p,Xt−p+1,...,Xt−1]∈RP×N×C,P+H个temporal attributes T m = [ T t − p m , T t − p + 1 m , . . . , T t + H − 1 m ] ∈ R P + H , m = 1 , . . . M T^m=[T_{t-p}^m,T_{t-p+1}^m,...,T_{t+H-1}^m] \in R^{P+H},m=1,...M Tm=[Tt−pm,Tt−p+1m,...,Tt+H−1m]∈RP+H,m=1,...M(有 T ∈ R ( P + H ) × M T \in R^{(P+H) \times M} T∈R(P+H)×M), 预构建的多图 { g b = ( V , E b , W b ) } b = 1 B \{g_b = (V,E_b,W_b)\}_{b=1}^B {gb=(V,Eb,Wb)}b=1B.
输出:next H time intervals的traffic state y = [ X t , X t + 1 , . . . , X t + H − 1 ] ∈ R H × N × C y=[X_t,X_{t+1},...,X_{t+H-1}] \in R^{H \times N \times C} y=[Xt,Xt+1,...,Xt+H−1]∈RH×N×C
3.2 Multi-head attention
注意机制可以看作是一个函数,将一个query和一组(key,value)对映射到一个输出中,其中query,key,value都是向量。输出是由这些值的加权和计算出来的。分配给每个值的权重是通过兼容(compatibility)函数计算的,compatibility函数的变量是query和相应的key。
本文使用的是 “scaled Dot-product Attention”,通过矩阵乘法并行处理所有query。给定queries, d k d_k dk维keys, d v d_v dv维values,attention是由以下计算:
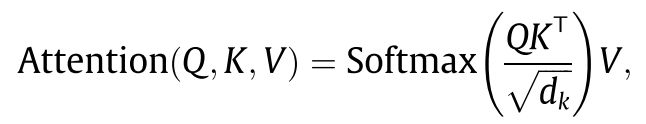
其中, Q ∈ R n 1 × d k Q \in R^{n_1 \times d_k} Q∈Rn1×dk, K ∈ R n 2 × d k K \in R^{n_2 \times d_k} K∈Rn2×dk, V ∈ R n 2 × d k V \in R^{n_2 \times d_k} V∈Rn2×dk.
为了使模型能够同时参与到不同的表示子空间中,常用的方法是采用多头注意。 d m o d e l d_{model} dmodel表示模型的特征size。给定原始queries Q ∈ R n 1 × d m o d e l Q \in R^{n_1 \times d_{model}} Q∈Rn1×dmodel,keys K ∈ R n 2 × d m o d e l K \in R^{n_2 \times d_{model}} K∈Rn2×dmodel, values V ∈ R n 2 × d m o d e l V \in R^{n_2 \times d_{model}} V∈Rn2×dmodel(自注意力,原始 Q K V QKV QKV相等即 X X X),多头注意力的计算过程如下:
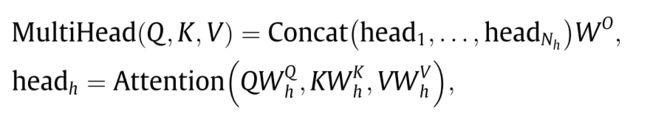
其中 N h N_h Nh 头的数量, W h Q ∈ R d m o d e l × d k W_h^Q \in R^{d_{model} \times d_k} WhQ∈Rdmodel×dk, W h K ∈ R d m o d e l × d k W_h^K \in R^{d_{model} \times d_k} WhK∈Rdmodel×dk, W h V ∈ R N h d m o d e l × d k W_h^V \in R^{N_hd_{model} \times d_k} WhV∈RNhdmodel×dk,本文中, d k = d v = d m o d e l / N h d_k = d_v = d_{model}/N_h dk=dv=dmodel/Nh
4 Meta Graph Transformer
4.1 Over pipeline
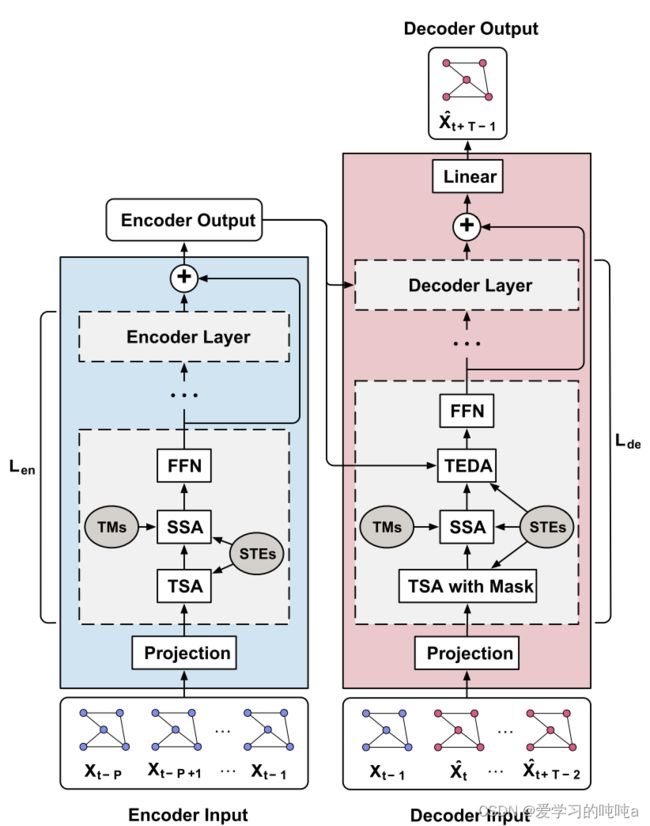
MGT模型的主要思想是在外部时空属性的指引下,通过构建时空异质性感知(STHA)注意层来学习复杂的时空相关性。总体过程如下图所示。模型为Encoder-Decoder, Encoder和Decoder都是由堆叠多个相同的sub-layers, 为了深度神经网络的高效学习,每一子层的输出跳接到最后一个子层的输出上(残差连接)。在子层中,三种注意层次被用来学习空间和时间的相关性。它们分别是时间自注意(TSA)、空间自注意(SSA)和时间编码器-解码器注意(TEDA)。Encoder和Decoder分别利用TSA和SSA对时间和空间依赖性进行建模。Decoder使用TEDAs将Decoder中的每个位置在时间上参与处理输入序列中的所有位置。所有注意层都具有多头结构,并利用从外部时空属性学习的时空嵌入(STEs)进行STHA操作。此外,SSAs是利用多个图(或等价地利用它们的转换矩阵(TMs))以捕获不同类型的空间相关性。为了使得Decoder看不见未来的信息,mask被用于TSA中。一般来说,MGT模型的流程如下所示:
- encoder的输入是历史traffic state X ∈ R P × N × C X \in R^{P \times N \times C} X∈RP×N×C ,首先将 X X X其映射为 X ( 0 ) ∈ R P × N × d m o d e l X^{(0)} \in R^{P \times N \times d_{model}} X(0)∈RP×N×dmodel(通过带有Relu函数的线形变换)
- 映射后的 X ( 0 ) X^{(0)} X(0) 输入 L e n L_{en} Len个block的 Encoder。第 l l l 个encoder层的输出为 X l X^l Xl,encoder的输出可表示为 X e n = ∑ l L e n X ( l ) ∈ R P × N × d m o d e l X_{en} = \sum_l^{L_{en}}X^{(l)} \in R^{P \times N \times d_{model}} Xen=∑lLenX(l)∈RP×N×dmodel
- 给定 X e n X_{en} Xen,decoder采用自回归的方式进行预测,decoder接受到 X t − 1 X_{t-1} Xt−1和之前的预测值 X ^ t , . . . , X ^ t + T − 2 \hat X_t,...,\hat X_{t+T-2} X^t,...,X^t+T−2与编码器类似,输入首先被投影到 P × N × d m o d e l {P \times N \times d_{model}} P×N×dmodel,然后输入 L e n L_{en} Len层的decoder。最后,线性变换将feature size 映射到C大小。最后一个时间点的输出即为next time interval X ^ t + T − 1 \hat X_{t+T-1} X^t+T−1
- 重复 H H H次 s t e p 3 step3 step3生成future traffic states.
4.2 STE
对于一个时空点 ( i , t ) (i,t) (i,t),节点 V i V_i Vi和time t t t,时空embedding为 C t i ∈ R m o d e l d C_t^i \in R_{model}^d Cti∈Rmodeld将外部空间和时间属性编码为固定长度的向量。如下图所示。
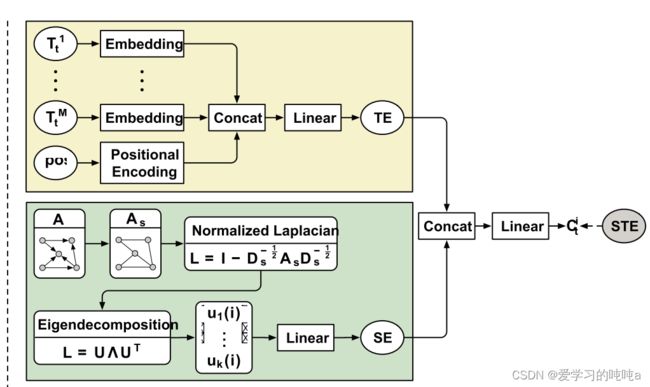
4.2.1 TE
除了附加在时间t上的所有时间属性 T t m m = 1 M {T_t^m}_{m=1}^M Ttmm=1M ,还有一个动态属性(相对于输入的时间位置pos,即输入序列的相对位置)应该被考虑。具体来说,时间t的时间嵌入(TE)的构建方法如下:
绝对时间:每个 T t m T_t^m Ttm是one-hot编码( N m N_m Nm维),然后总共使用M个可学习矩阵将这些向量线性转换为长度为 d m o d e l d_{model} dmodel的向量。
**相对时间:**pos也被编码为长度 d m o d e l d_{model} dmodel的向量。
然后concatente,再通过线性变换,最终得到temporal embedding U t ∈ R m o d e l d U_t \in R_{model}^d Ut∈Rmodeld
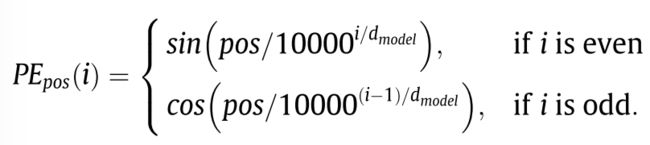
4.2.2 Spatial Embedding
是由论文"A Generalization of Transformer Networks to Graphs"的启发,图的结构信息被编码到空间嵌入(SE)是通过一个经典的图嵌入技术——特征映射完成的。为了满足要求,通过定义无向图 A s = m a x ( A , A T ) A_s = max(A,A^T) As=max(A,AT),特征映射算法如下:
首先,归一化Lap矩阵,然后特征分解。最后得到 n o d e V i node V_i nodeVi的k维度embedding Z ^ i \hat Z_i Z^i。计算完之后,通过线性变换得到最终的spatial embedding Z i Z_i Zi.
4.2.3 STE
C t i C_t^i Cti 是通过 Z i Z_i Zi和 U t U_t Ut的concatenate之后,再经过linear layer得到的。
4.3 transition Matrices
4.3.1 多图构造
交通网络本身可以看作是一个简单的加权图,其中所有边的权值都为1。这样的图也称为连通性图。在给定距离信息的情况下,可以对图的边权值进行修改,以反映节点之间的真实距离。从 v j v _j vj到 v i v_i vi的基于距离的权值的一般定义如下:
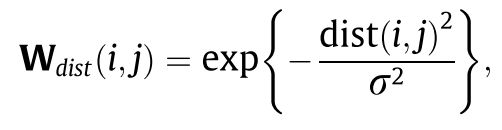
除了地理连通性,功能相似性也是探索空间相关性的关键因素。虽然有些节点在现实中可能没有连接,甚至彼此相距很远,但它们可能在交通网络中共享相同的功能(商业中心、住宅区等),因此符合类似的交通模式。 X h i s t i ∈ R p ′ c X_{hist}^i \in R^{p'c} Xhisti∈Rp′c 是node V i V_i Vi的历史traffic state( p ′ p' p′ 是训练集中时间段的数量), V i V_i Vi和 V j V_j Vj的相似度计算方式如下。给定阈值,小于阈值为0可构造矩阵。

另一个有用的图是基于一些交通流数据集提供的出发地-目的地(OD)信息。通常,从KaTeX parse error: Expected group after '_' at position 3: vj_̲到 v i v_i vi的基于od的相关性可以定义为. c o u n t ( i , j ) count(i,j) count(i,j)表示i到j的所有记录数。
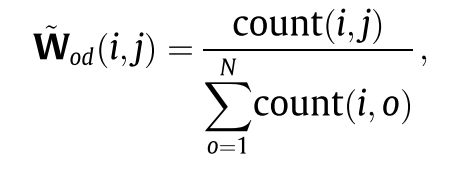
4.3.2 transition matrices
给定 g b = ( V , E b , W b ) g_b=(V,E_b,W_b) gb=(V,Eb,Wb),transition matrix S b ∈ R N × N S_b \in R^{N \times N} Sb∈RN×N通过以下方式计算可得:
W b W_b Wb的对角元素设置为1,然后对行进行归一化。


4.4 Encoder
4.4.1 TSA
最容易想到的做法:
Q = K = V Q=K=V Q=K=V,直接将self-attention用于第 l − 1 l-1 l−1层的 H l − 1 ∈ R P × N × d m o d e l H^{l-1} \in R^{P \times N \times d_{model}} Hl−1∈RP×N×dmodel,即
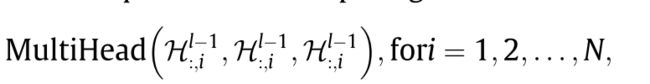
其中 H : , i l − 1 ∈ R P × d m o d e l H_{:,i}^{l-1} \in R^{P \times d_{model}} H:,il−1∈RP×dmodel 是node V i V_i Vi的时序特征,所有节点共享参数。这样不合理,因为共享机制忽略了交通状态的动力学在时间和位置上变化很大的特性。有必要考虑时空特性。为每个head创建一个带有隐藏层的多层感知器,该网络收到 C t i C_t^i Cti作为输入,生成三个映射矩阵用于转换 H t , i l − 1 ∈ R m o d e l d H_{t,i}^{l-1} \in R_{model}^d Ht,il−1∈Rmodeld的query,key和value vector。(三个W矩阵是通过MLP计算出来的)
4.4.2 SSA
与TSA相似,设计了一种基于STS引导的多头多图SSA进行空间特征学习。使用“多图”可以直观地看出,与其关注所有的空间位置,不如关注那些通过领域知识与中心节点更有可能关联的节点。因此多图 { g b } b = 1 B \{g_b\}_{b=1}^B {gb}b=1B(或者其等价转换矩阵 { S b } b = 1 B \{S^b\}_{b=1}^B {Sb}b=1B),被利用捕获不同类型节点间关系,去执行稀疏自注意。更具体一点,对每一个图 g b g_b gb,node V i V_i Vi将参与近邻 { V j ∣ j ∈ N i b } \{V_j|j \in N_i^b\} {Vj∣j∈Nib} N h N_h Nh次,从而得到 V i V_i Vi的总共 B N h BN_h BNh向量。然后通过concatenation和线性变换将这些向量进行融合。
此外,通过element-wise将转移矩阵中的动态注意系数和静态值联合确定相邻节点的权值,可以充分利用领域知识。为了保证STHA的正常运行,在注意参数的生成过程中还利用了STEs。和TSA一样,这里也采用了剩余连接和层归一化。

4.4.3 FFN
前馈网络(FNN)是一个位置变换层,每个时空点的参数都是共享的, 给定任意位置的特征向量 x ∈ R m o d e l d x \in R_{model}^d x∈Rmodeld,FNN的计算公式如下:
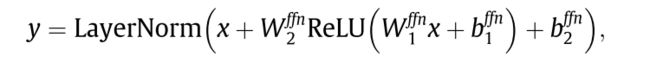
4.5 Decoder
Decoder堆栈有输出投影层、具有跳接的相同Encoder层和用于预测的线性层。每个Decoder层由四个组件组成,即TSA with Mask、SSA、TEDA和FFN。SSA和FFN的结构与编码器相同,而TSA with mask,以防止未来的时间步参与运算。TEDA作为连接Encoder输出和Decoder各层的桥梁,能够从历史数据中进行自适应特征学习。
4.5.1 TSA with mask
带mask的TSA工作原理与4.4.1节中描述的TSA基本相同。唯一的区别是,mask会在scaled dot-product之后添加。mask 是一个 T × T T \times T T×T的矩阵,上对角元素为负无穷,其他元素为0.然后:
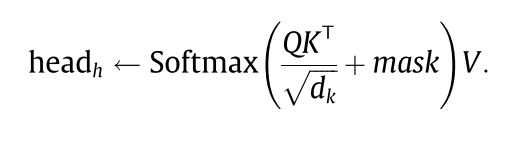
4.5.2 TEDA
TEDA是为Decoder创建的,以自适应地参与沿时间维度的Encoder特征。在这种情况下,query来自Decoder,而key和value来自Encoder。与算法1中相同,可以根据Encoder的输出 X e n ∈ R P × N × d m o d e l X_{en} \in R^{P \times N \times d_{model}} Xen∈RP×N×dmodel计算出多头key和value。


这些key和value然后被Decoder中的每个TEDA使用来执行STS-guide的时间注意操作。TEDA的详细信息显示在如下。

5. Experiments
有空再续
总结
考虑了多图,不用GCN直接将图拓扑信息和相对时间以及绝对时间放到self-attention,但是时间维度和空间维度分开算的, 合并计算是不是更好呢?Decoder部分的是不是输入时间信息会更好?还是用的autoregressive,考虑non-autoregressive是不是更好?