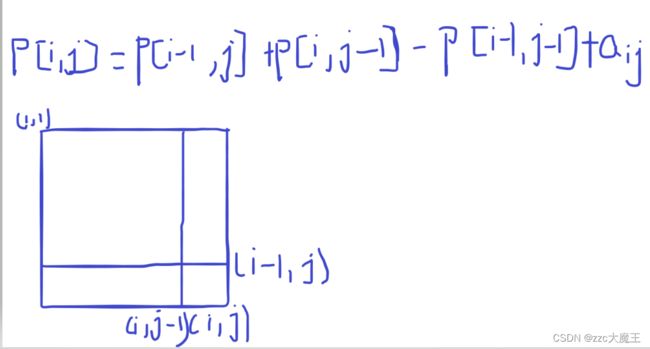2022年第十三届蓝桥杯省赛C++B组【真题解析】
目录
第一题:九进制转十进制
第二题:顺子日期
第三题:刷题统计
第四题:修剪灌木
第五题:X进制减法
第六题:统计子矩阵
第七题:积木画
第八题:扫雷
第九题:李白打酒加强版
第十题:砍竹子
第一题:九进制转十进制
按权展开相加法。
AC代码
#include
using namespace std;
int main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(false);
cout<<2*pow(9,3)+2*pow(9,1)+2;
return 0;
}
输出1478
第二题:顺子日期
这道题当时在做的时候,所有人都在纠结012到底是不是,以题目而言,他说20220123出现了一个顺子日期,因为出现了一个顺子:123,而没有说出现了两个顺子012,123,所以012应该不算。结果显而易见我们的语文不太好,答案的要求是012也是顺子。
AC代码
#include
using namespace std;
int m[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int ans;
int main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(false);
//显然2022年不是闰年,则2月只有28天
string year="2022";
string date;
int mm=1,dd=1;
while(true){
if(dd==m[mm]){
mm++;
dd=1;
if(mm==13&&dd==1)break;
}
date="";
date+=year;
if(mm<10){
date+='0';
date+= to_string(mm);
}else
date+= to_string(mm);
if(dd<10){
date+='0';
date+= to_string(dd);
}else
date+= to_string(dd);
for(int i=0;i 这道题手算似乎更加方便。
第三题:刷题统计
范围这么大一眼long long。
简单想法,模拟日期然后慢慢遍历。
TL代码
#include
using namespace std;
using ll=long long;
ll a,b,n,sum;
int main() {
cin>>a>>b>>n;
for(ll i=1; ;i++) {
if(i%7!=6 && i%7!=0) sum+=a;
else sum+=b;
if(sum>=n) {
cout< 但是对于这么大的数据范围肯定会超时。
不难想到每周做题量是a*5+b*2,那么(n/每周做题量)就是过去了多少周可以做掉n个题目,如果存在余数,遍历一周让余数变成0。
AC代码
#include
using namespace std;
using ll=long long;
ll a,b,n,ans,hasDo,weekDo;
int main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(false);
cin>>a>>b>>n;
weekDo=a*5+b*2;
if(n=n)break;
}
}else{
ans=n/weekDo;
hasDo=weekDo*ans;
ans*=7;
for(int i=1;i<=7;i++){
if(hasDo>=n)break;
if(i==6||i==7)hasDo+=b;
else hasDo+=a;
ans++;
}
}
cout< 第四题:修建灌木
对于a1~an个灌木,有位神必人物会从a1~an然后an~a1去把他们砍掉,然而灌木生命力旺盛,不管是否被砍掉都会变长1点,问你max{a1,a2,a3,a4,...,an}
然而根据题目可以知道初始高度都可以认为是0,那么最高高度取决于神必人物来回走的距离,并且最高的一定是a1或者an。
AC代码
#include
using namespace std;
int n,a[10005];
int main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(false);
cin>>n;
if(n==1)cout<<1;
else{
int t=(n-1)*2;
int l=1,r=n;
while(l<=r){
a[l++]=t;
a[r--]=t;
t-=2;
}
for(int i=1;i<=n;i++)
cout< 第五题:X进制减法
给你两个X进制数A和B, 在保证A和B在X进制合法的情况下,输出min(A-B)
基本和第一题没什么区别,依旧是按权展开相加法,但是要求每一位的权尽可能小,也就是取两位之中最大的那一个然后加1使其合法,所以题目给的N是没有用的。
比较难想到点的是,比如32这个十进制,3是由2变过来的,若2这个位是十进制,则3一定是30,所以前一位的权是由后一位的进制确定的,那么累乘后面的所有进制就是这个当前这个进制的总权。
AC代码
#include
using namespace std;
using ll=long long;
const int MAXN=100005;
const ll MOD=1000000007;
ll ans,base=1;
ll n,an,bn,a[MAXN],b[MAXN],w;
void scan(){
cin>>n;//no use
cin>>an;
for(int i=an;i>=1;i--)
cin>>a[i];
cin>>bn;
for(int i=bn;i>=1;i--)
cin>>b[i];
}//低到高
int main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(false);
scan();
for(int i=1;i<=an;i++){
w=max(a[i],b[i])+1;
if(w<2)w=2;
ans=(ans+(a[i]-b[i])*base)%MOD;//ans放在里面,满足运算法则
base=(base*w)%MOD;
}
cout< 第六题:统计子矩阵
一眼暴力
TL代码
#include
using namespace std;
const int MAXN=500;
int n,m,k,ans,a[MAXN][MAXN];
inline void scan(){
cin>>n>>m>>k;
for(int i=0;i>a[i][j];
}
}
}
int getSum(int x1,int y1,int x2,int y2){
int sum=0;
for(int i=x1;i<=x2;i++)
for(int j=y1;j<=y2;j++)
sum+=a[i][j];
return sum;
}
int main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(false);
scan();
//第一个点
for(int i=0;i 很经典的超时代码,getSum函数每次都在不停的求和,有没有类似于前缀和一样的东西让他变成O(1)复杂度的查询呢,二维前缀和。
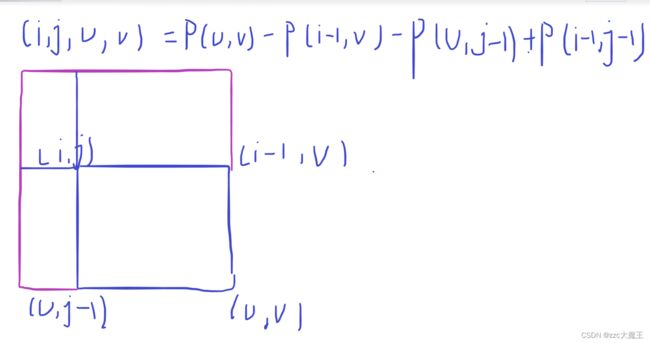
定义p[i][j]为A[1][1]~A[i][j]这个矩阵的和,不难得到如下式子那么依然画图可得,取到两点(i,j)到(u,v)两点的矩阵和如下所示。
这样优化之后我们照样喜提TL代码一只。
TL代码2
#include
using namespace std;
const int MAXN=501;
int ans,n,m,k,p[MAXN][MAXN];
inline void scan(){
cin>>n>>m>>k;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>p[i][j];
p[i][j]+=p[i-1][j]+p[i][j-1]-p[i-1][j-1];
}
}
}
int getSum(int i,int j,int u,int v){
return p[u][v]-p[u][j-1]-p[i-1][v]+p[i-1][j-1];
}
int main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(false);
scan();
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
for(int l=i;l<=n;l++){
for(int i1=j;i1<=m;i1++){
if(getSum(i,j,l,i1)<=k)ans++;
}
}
}
}
cout< 还是超时那接下来考虑选点方式,不能简单的直接暴力,如果一个大矩阵可行,那么他的小矩阵必然可行,因此这里使用大名鼎鼎的尺取法(Two Point)来减少遍历次数。
AC代码
#include
using namespace std;
const int MAXN=501;
int n,m,k,p[MAXN][MAXN];
long long ans;
inline void scan(){
cin>>n>>m>>k;
for(int i=1;i<=n;i++){//二维前缀和
for(int j=1;j<=m;j++){
cin>>p[i][j];
p[i][j]+=p[i-1][j]+p[i][j-1]-p[i-1][j-1];
}
}
}
inline int getSum(int i,int j,int u,int v){
return p[u][v]-p[u][j-1]-p[i-1][v]+p[i-1][j-1];
}
int main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(false);
scan();
//尺取法,限定上下边界,蠕动左右边界,减少判断次数
for(int i=1;i<=n;i++){//上边界
for(int j=i;j<=n;j++){//下边界
for(int col_l=1,col_r=1;col_r<=m;col_r++){//左右蠕动边界
while(col_l<=col_r&& getSum(i,col_l,j,col_r)>k)col_l++;
if(col_l<=col_r)ans+=col_r-col_l+1;//如果区间合法,那么说明此矩阵和必定小于等于k,所以子矩阵也合法
}
}
}
cout< 第七题:积木画
洛谷传送门 覆盖墙壁 - 洛谷
如果没有思路可以考虑对N取前几个值,然后找出规律,这种题肯定有规律!
很明显的一道状态压缩DP,找出状态与状态之间的关系,确定起点,那这道题不就做出来了%%?
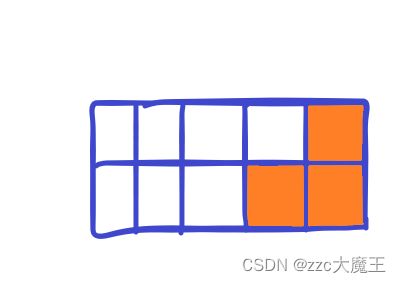
对于这样一个墙壁,我们定义f[n]为前n*2个墙壁被填满的方案数。
如果有这样两个墙壁,最后一列和最后两列都没填满,那么他们能被填上的情况只能是这样,也就是说f[n]=f[n-1]+f[n-2]这个式子肯定存在,但是不一定完整,因为我们没有举出所有情况。同时也不要重复举状况(只要基本状态),比如已经写了用I来铺满最后一个,再写一个II就没有意义了,因为II包含在I里面。
不好理解的话以经典走楼梯为例。
你面前有100格台阶,你只能走1步或者2步。
定义dp[n]为走完n个台阶的总方法数
那么必然有dp[n]=dp[n-1]+dp[n-2]
因为dp[n]这个状态只能由dp[n-1]这个状态走一步 和 dp[n-2]这个状态走两步汇总过来
再举个例子!
比如已知你有五种方法可以到达第n个台阶,你只能走一步,问你有多少种方法可以到n+1个台阶
那不就是5种呗。
然后以画图的形式找出所有状况就可以了,这种情况比较特殊,要另起数组维护,详细看洛谷题解。
定义G[n]为前(n-1)*2个墙壁都被填满,n处被填了一块的情况
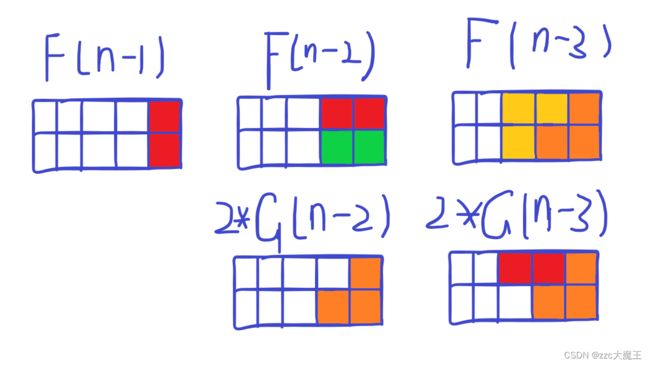
不难得到全部情况
不难发现G[n-2]的情况被F[n-3]和G[n-3]全部包含在内,即G[n-2]=F[n-3]+G[n-3],
即G[n]=F[n-1]+G[n-1]
另一边F[n]=F[n-1]+F[n-2]+2*G[n-2]
为什么F[n]后面不加F[n-3]?你没发现被G包含在内了?(要选最基础的,不要选叠加态%%%)AC代码
#include
using namespace std;
using ll=long long;
const ll MOD=1000000007;
const int MAXN=10000000;
ll n,f[MAXN+1],g[MAXN+1];
int main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(false);
cin>>n;
f[1]=1;g[1]=1;
f[2]=2;g[2]=2;
for(int i=3;i<=n;i++){
g[i]=(f[i-1]+g[i-1])%MOD;
f[i]=((f[i-1]+f[i-2])%MOD+2*g[i-2]%MOD)%MOD;
}
cout< 第八题:扫雷
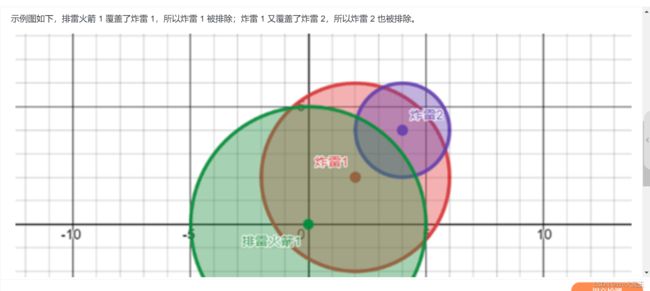
这道题之所以用不出任何算法只知道暴力,那是因为没有仔细读题和题刷的不够多!
因为炸弹存在连锁反应,所以我们可以建图,并且很明显是一个有向图,比如样例中炸弹1可以引爆炸弹2,但是炸弹2不能引爆炸弹1。
代码过不了最后一个样例,并且还是答案错误。
留坑待填
?代码
#include
using namespace std;
using ll=unsigned long long;
const int MAXNM = 5e4;
ll n,m,ans;
struct Node{
ll x,y,r;
};
Node mine[MAXNM+1];//n个炸弹
Node cleaner[MAXNM+1];//m个排雷火箭
vectorvertexMine[MAXNM+1];
vectorvertexCleaner[MAXNM+1];
bitsetvis;//炸弹是否被访问
stackdfs;
inline void scan(){
cin>>n>>m;
for(int i=0;i>mine[i].x>>mine[i].y>>mine[i].r;
for(int i=0;i>cleaner[i].x>>cleaner[i].y>>cleaner[i].r;
}
inline ll centerDistance(Node node1,Node node2){
return (node1.x-node2.x)*(node1.x-node2.x)+(node1.y-node2.y)*(node1.y-node2.y);
}
inline void build(){
//炸弹之间的关系
for(int i=0;icenterDistance(mine[i],mine[j])){
vertexMine[i].push_back(j);
}
}
}
//火箭和炸弹之间的关系
for(int i=0;icenterDistance(cleaner[i],mine[j])){
vertexCleaner[i].push_back(j);
}
}
}
}
int main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(false);
scan();
build();
for(int i=0;i 第九题:李白打酒加强版
如果N+M小于13的话那么用全排列还是能勉强做一做的,但是这道题很明显也存在规律,而且相比第七题积木画更加简单。
对有关系的状态全部进行定义,如果需要优化再做考虑。
定义 f[i][j][k] 为 遇到店i次,遇到花j次,还剩k斗酒 的所有方案
那么答案就是f[n][m-1][1]
很显然f[i][j][k]=f[i-1][j][k/2]+f[i][j-1][k+1](遇到店+遇到花)AC代码
#include
using namespace std;
using ll=long long;
const ll MOD=1000000007;
ll n,m,ans;
ll f[105][105][105];
int main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(false);
cin>>n>>m;
f[0][0][2]=1;//不管怎么样必然会有一种初始方案。
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
for(int k=0;k<=m;k++){
//遇到花
if(j&&k)f[i][j][k]=(f[i][j][k]+f[i][j-1][k+1])%MOD;
//遇到店
if(i&&k%2==0)f[i][j][k]=(f[i][j][k]+f[i-1][j][k/2])%MOD;
}
}
}
//因为没有酒遇到花是不合法的,所以循环的时候没有执行f[][m][0]的所有情况
//因为最后一步必须是遇到花,所以f[n][m-1][1]的值等于我们想要的f[n][m][0]
cout< 对于代码中两个if的解释,遇到花的时候酒不能为空 即j&&k
遇到店的时候是i k%2是相对k/2来说的
如果k/2,k=3,那么算出来为1,这两个毫无关系,1要对应的是2,即k%2。第十题:砍竹子
简单的灵能传输(2019蓝桥杯省赛C++B组最后一题)我都做不出来,现在反而来了一个困难的砍竹子......
然而看完题面之后居然感觉是一道水题,只要保证每次魔法都施展在【最高且连续高度相同】,那么这道题就解出来了。
难点在于怎样可以快速求出哪一个区间是最长并且最高的
优先队列就是其中一个解,建立大根堆,每次都能取到最大的
选中最大的施展魔法,然后pop掉
如果有和它高度一样的,那么就是接下来被pop的那一位AC?代码
#include
using namespace std;
using ll=long long;
ll h,hnew,ans,n,rnk;
priority_queue,vector>,less>>q;
//大根堆,即大数字优先级高
int main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++){
cin>>h;
if(h!=1)q.push({h,i});//高度为1就不用砍了
}
while(!q.empty()){
h=q.top().first,rnk=q.top().second;
q.pop();
hnew= sqrt(h/2+1);
if(hnew!=1)q.push({hnew,rnk});
while(!q.empty()&&q.top().first==h&&q.top().second==rnk-1){
rnk--;
q.pop();
if(hnew!=1)
q.push({hnew,rnk});
}
ans++;
}
cout< 写了个问号是因为在蓝桥云课上代码过不去,在其他收录的OJ网站里面反而过了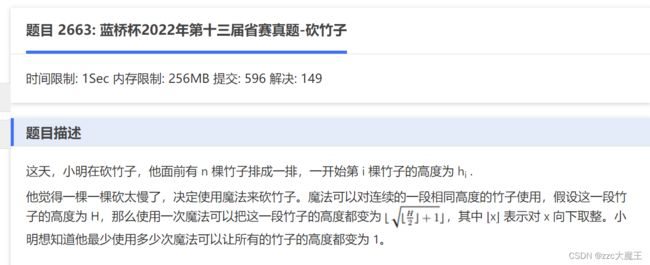
个人认为代码的思想应该是没问题的。因为蓝桥网课上提交一次会出现一个输入输出,所以我尝试了DDOS,但是样例有点多,失败了。
失败的DDOS代码
#include
using namespace std;
using ll=unsigned long long int;
ll h,hnew,ans,n,rnk;
priority_queue,vector>,less>>q;
//大根堆,即大数字优先级高
int main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(false);
cin>>n;
if(n==200000){
ll ddos;
cin>>ddos;
if(ddos==73729233413158469)cout<<881638;
if(ddos==340479921469247977)cout<<881664;
if(ddos==708432425852105668)cout<<881811;
if(ddos==6114973206075427)cout<<880801;
if(ddos==801221584540798726)cout<<882354;
if(ddos==814367781177829485)cout<<882382;
if(ddos==613106843417097304)cout<<881790;
if(ddos==918124662398042823)cout<<881726;
return 0;
}
for(int i=1;i<=n;i++){
cin>>h;
if(h!=1)q.push({h,i});//高度为1就不用砍了
}
while(!q.empty()){
h=q.top().first,rnk=q.top().second;
q.pop();
hnew= sqrt(h/2+1);
if(hnew!=1)q.push({hnew,rnk});
while(!q.empty()&&q.top().first==h&&q.top().second==rnk-1){
rnk--;
q.pop();
if(hnew!=1)
q.push({hnew,rnk});
}
ans++;
}
cout< 我甚至去找了各种地方写着成功的代码,然而提交都显示答案错误。
有人提交能过,但是都没写题解(悲)