【人工智能】机器学习基础(QDU)
- 【人工智能】不确定性推理(QDU)
- 【人工智能】传统机器学习算法(QDU)
- 【人工智能】非线性分类器(QDU)
- 【人工智能】机器学习基础(QDU)
- 【人工智能】深度学习(QDU)
最小二乘法
一般用于计算损失函数取最值时的解。
两个参数的最小二乘法
定义2D样本的回归模型如下:
2D样本:一般由一个特征决定标签/函数值,因此参数的确定需要常数项系数和一次项系数,即两个因素影响损失函数值,所以称为2D
l o s s = ∑ i n ( y i − w 0 − w 1 x ) 2 loss = \sum_i^n (y_i-w_0-w_1x)^2 loss=i∑n(yi−w0−w1x)2
要让损失函数 l o s s loss loss取得最小值需要求导:
∂ l o s s ∂ w 0 = 2 ∑ i n ( y i − w 0 − w 1 x i ) ( − 1 ) = 0 ∂ l o s s ∂ w 1 = 2 ∑ i n ( y i − w 0 − w 1 x i ) ( − X i ) = 0 \frac{\partial loss}{\partial w_0} = 2\sum_i^n(y_i-w_0-w_1x_i)(-1) = 0 \\ \frac{\partial loss}{\partial w_1} = 2\sum_i^n(y_i-w_0-w_1x_i)(-X_i) = 0 ∂w0∂loss=2i∑n(yi−w0−w1xi)(−1)=0∂w1∂loss=2i∑n(yi−w0−w1xi)(−Xi)=0
使用克莱姆法求解如下:
克莱姆法则:
记n元非齐次线性方程组的系数矩阵为 A A A,自变量矩阵(列向量)为 X X X,常数项矩阵(列向量)为 B B B。
记系数矩阵 A A A的行列式为 D = ∣ A ∣ D = |A| D=∣A∣ 。
当 D ≠ 0 D≠0 D=0时,有唯一解, X = A − 1 B X = A^{-1}B X=A−1B。其中 X X X由 x i x_i xi构成, x i = D j D x_i = \frac{D_j}{D} xi=DDj ( j = 1 , 2 , . . . , n ) (j = 1,2,..., n) (j=1,2,...,n),其中 D j D_j Dj是把 D D D中第 j j j列元素对应地换成常数项而其余各列保持不变所得到的行列式。
求解过程:
由上面两个偏导为零可以列出2元线性方程组:
{ n w 0 + ∑ i n x i w 1 = ∑ i n y i ∑ i n x i w 0 + ∑ i n x i 2 w 1 = ∑ i n x i y i \begin{cases} nw_0 + \sum_i^n x_i w_1 = \sum_i^ny_i \\ \sum_i^n x_i w_0 + \sum_i^n x_i^2 w_1 = \sum_i^nx_iy_i \end{cases} {nw0+∑inxiw1=∑inyi∑inxiw0+∑inxi2w1=∑inxiyi
可得:
D = ∣ n ∑ x i ∑ x i ∑ x i 2 ∣ = n ∑ x i 2 − ( ∑ x i ) 2 D 0 = ∣ ∑ y i ∑ x i ∑ x i y i ∑ x i 2 ∣ = ∑ x i 2 ∑ y i − ∑ x i ∑ x i y i D 1 = ∣ n ∑ y i ∑ x i ∑ x i y i ∣ = n ∑ x i y i − ∑ x i ∑ y i D = \left| \begin{matrix}{} n & \sum x_i \\ \sum x_i & \sum x_i^2 \end{matrix}\right| = n\sum x_i^2 - (\sum x_i)^2\\ D_0 = \left| \begin{matrix}{} \sum y_i & \sum x_i \\ \sum x_i y_i & \sum x_i^2 \end{matrix}\right| = \sum x_i^2 \sum y_i - \sum x_i \sum x_i y_i\\ D_1 = \left| \begin{matrix}{} n & \sum y_i \\ \sum x_i & \sum x_iy_i \end{matrix}\right| = n\sum x_iy_i - \sum x_i\sum y_i D=∣∣∣∣n∑xi∑xi∑xi2∣∣∣∣=n∑xi2−(∑xi)2D0=∣∣∣∣∑yi∑xiyi∑xi∑xi2∣∣∣∣=∑xi2∑yi−∑xi∑xiyiD1=∣∣∣∣n∑xi∑yi∑xiyi∣∣∣∣=n∑xiyi−∑xi∑yi
最终可得:
w 0 = ∑ x i 2 ∑ y i − ∑ x i ∑ x i y i n ∑ x i 2 − ( ∑ x i ) 2 w 1 = n ∑ x i y i − ∑ x i ∑ y i n ∑ x i 2 − ( ∑ x i ) 2 w_0 = \frac{\sum x_i^2 \sum y_i - \sum x_i \sum x_i y_i}{n\sum x_i^2 - (\sum x_i)^2} \\ w_1 = \frac{n\sum x_iy_i - \sum x_i\sum y_i}{n\sum x_i^2 - (\sum x_i)^2} \\ w0=n∑xi2−(∑xi)2∑xi2∑yi−∑xi∑xiyiw1=n∑xi2−(∑xi)2n∑xiyi−∑xi∑yi
最小二乘法的矩阵表达形式
可用于求解多参数的最值。
为了更佳地展示过程,我们设损失函数为 l o s s = ∣ ∣ A x − b ∣ ∣ 2 2 loss = ||Ax-b||_2^2 loss=∣∣Ax−b∣∣22,其中 A A A表示样本数据的特征值, x x x表示参数即求解目标, b b b表示样本数据特征值对应的标签/函数值。求损失函数取最小值时对应的解,此解即为模型中的参数。
∣ ∣ x ∣ ∣ 2 ||x||_2 ∣∣x∣∣2为二范数,又称欧几里得范数。详见0 范数、1 范数、2 范数的区别 - 知乎
∣ ∣ A x − b ∣ ∣ 2 2 = ( A x − b ) T ∗ ( A x − b ) = x T A T A x − b T A x − x T A T b + b T b || Ax - b ||_2^2 \\ = (Ax−b)^T∗(Ax−b) \\ = x^TA^TAx−b^TAx−x^TA^Tb+b^Tb ∣∣Ax−b∣∣22=(Ax−b)T∗(Ax−b)=xTATAx−bTAx−xTATb+bTb
令其对 x x x的导数等于零可得:
对其求导需要一些有关矩阵/向量求导的知识:
① ∂ x T a ∂ x = a T x x = a \frac{∂x^T a}{∂x} = \frac{a^Tx}{x} = a ∂x∂xTa=xaTx=a
② ∂ x T A x ∂ x = A x + A T x \frac{∂x^TAx}{∂x} = Ax+A^Tx ∂x∂xTAx=Ax+ATx
③ A T A A^TA ATA是对称的
④ 如果矩阵 A A A是对称的, A x + A T x = 2 A x Ax+A^Tx=2Ax Ax+ATx=2Ax
∂ x T A T A x − b T A x − x T A T b + b T b ∂ x = 0 ∂ x T A T A x ∂ x − ∂ b T A x + x T A T b ∂ x + ∂ b T b ∂ x = 0 \frac{∂x^TA^TAx−b^TAx−x^TA^Tb+b^Tb}{∂x} = 0 \\ \frac{∂x^TA^TAx}{∂x} - \frac{∂b^TAx+x^TA^Tb}{∂x} + \frac{∂b^Tb}{∂x} = 0 \\ ∂x∂xTATAx−bTAx−xTATb+bTb=0∂x∂xTATAx−∂x∂bTAx+xTATb+∂x∂bTb=0
其中, ∂ x T A T A x ∂ x = ② A T A x + ( A T A ) T x = ③ 2 A T A x \frac{∂x^TA^TAx}{∂x} \overset{②}= A^TAx + (A^TA)^Tx \overset{③}= 2A^TAx ∂x∂xTATAx=②ATAx+(ATA)Tx=③2ATAx
∂ b T A x + x T A T b ∂ x = ∂ ( b T A ) x + x T ( A T b ) ∂ x = ① A T b + A T b = 2 A T b \frac{∂b^TAx + x^TA^Tb}{∂x} \overset{}= \frac{∂(b^TA)x + x^T(A^Tb)}{∂x} \overset{①}= A^Tb + A^Tb = 2A^Tb ∂x∂bTAx+xTATb=∂x∂(bTA)x+xT(ATb)=①ATb+ATb=2ATb
∂ b T b ∂ x = 0 \frac{∂b^Tb}{∂x} = 0 ∂x∂bTb=0
因此, 原 式 = 2 A T A x − 2 A T b = 0 原式=2A^TAx−2A^Tb=0 原式=2ATAx−2ATb=0,解得 x = ( A T A ) − 1 A T b x=(A^TA)^{−1}A^Tb x=(ATA)−1ATb
最小二乘法的局限性
只有当矩阵 A A A的每一列都是线性不相关的,矩阵 A T A A^TA ATA才是可逆的。 最小二乘法才存在唯一的最优解 x = ( A T A ) − 1 A T Y x=(A^TA)^{−1}A^TY x=(ATA)−1ATY。
- A T A A^TA ATA不可逆时,无法求解
- 当特征维数大时, A T A A^TA ATA求逆困难
因此引入“梯度下降法”。
梯度下降法
梯度即是某一点最大的方向导数,沿梯度方向函数有最大的变化率(正向增加,逆向减少)。
代价函数沿梯度的负方向下降最快。
梯度下降法(Gradient Descent,GD)
梯度下降法步骤
规定:
h θ ( x ) = θ 0 + θ 1 x 1 + . . . + θ n x n = ∑ i = 0 n θ i x i = θ T x h_\theta(x) = \theta_0 + \theta_1x_1 + ... + \theta_nx_n = \sum_{i=0}^n\theta_ix_i=\theta^Tx hθ(x)=θ0+θ1x1+...+θnxn=∑i=0nθixi=θTx
设 l o s s ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 loss(\theta) = \frac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 loss(θ)=21∑i=1m(hθ(x(i))−y(i))2
其中 x ( i ) = ( x 1 , x 2 , . . . , x n ) T x^{(i)} = (x_1, x_2, ... , x_n)^T x(i)=(x1,x2,...,xn)T, y ( i ) y^{(i)} y(i) 为特征值{ x 1 , x 2 , . . . , x n x_1,x_2, ..., x_n x1,x2,...,xn}对应的真实值。
- 首先对 θ \theta θ 赋初值,这个值可以是随机的,也可以让 θ \theta θ 是 一个全零的向量。
- 计算梯度: ∂ l o s s ( θ ) ∂ θ j = ∂ ∂ θ j 1 2 ∑ i = 1 m ( θ T x ( i ) − y ( i ) ) 2 = ∑ i = 1 m ( θ T x ( i ) − y ( i ) ) x j ( i ) \frac{∂loss(\theta)}{∂\theta_j} = \frac{∂}{∂\theta_j} \frac{1}{2}\sum_{i=1}^m(\theta^Tx^{(i)}-y^{(i)})^2 = \sum_{i=1}^m(\theta^Tx^{(i)}-y^{(i)})x_j^{(i)} ∂θj∂loss(θ)=∂θj∂21∑i=1m(θTx(i)−y(i))2=∑i=1m(θTx(i)−y(i))xj(i)
- 修改参数值: θ j = θ j − α ∂ l o s s ( θ ) ∂ θ j , ∀ j \theta_j = \theta_j - \alpha\frac{∂loss(\theta)}{∂\theta_j}, ∀j θj=θj−α∂θj∂loss(θ),∀j,其中 α \alpha α表示学习步长,也就是每次按照梯度减少的方向变化多少。
- 按照(3)迭代更新 θ \theta θ值,直至收敛或者 θ \theta θ 值的改变小于设定的阈值。
局限性
- 梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。
- 由于有局部最优解的风险,需要多次用不同初始值运行算法。
- 步长太大,会导致迭代过快,甚至有可能错过最优解。步长太小,迭代速度太慢,很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。
批量梯度下降法(Batch Gradient Descent,BGD)
批量梯度下降法是最原始的形式,它是指在每一次迭代时使用所有样本来进行梯度的更新。
(1)对目标函数求偏导:
∂ l o s s ( θ ) ∂ θ j = ∂ ∂ θ j 1 2 ∑ i = 1 m ( θ T x ( i ) − y ( i ) ) 2 = ∑ i = 1 m ( θ T x ( i ) − y ( i ) ) x j ( i ) \frac{∂loss(\theta)}{∂\theta_j} = \frac{∂}{∂\theta_j} \frac{1}{2}\sum_{i=1}^m(\theta^Tx^{(i)}-y^{(i)})^2 = \sum_{i=1}^m(\theta^Tx^{(i)}-y^{(i)})x_j^{(i)} ∂θj∂loss(θ)=∂θj∂21i=1∑m(θTx(i)−y(i))2=i=1∑m(θTx(i)−y(i))xj(i)
其中 i = 1 , 2 , . . . , m i=1,2,...,m i=1,2,...,m 表示样本数, j = 0 , 1 , . . . , n j=0,1,...,n j=0,1,...,n 表示特征数,这里我们使用了偏置项 x 0 ( i ) = 1 x^{(i)}_0=1 x0(i)=1 。
(2)每次迭代对参数进行更新:
θ j = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j = \theta_j - \alpha\frac{1}{m} \sum_{i=1}^m (h_\theta(x^{(i)})-y^{(i)} )x_j^{(i)} θj=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)
注意这里更新时存在一个求和函数,即为对所有样本进行计算处理,可与下文SGD法进行比较。
优点:
- 一次迭代是对所有样本进行计算,此时利用矩阵进行操作,实现了并行。
- 由全数据集确定的方向能够更好地代表样本总体,从而更准确地朝向极值所在的方向。当目标函数为凸函数时,BGD一定能够得到全局最优。
缺点:
当样本数目 m m m 很大时,每迭代一步都需要对所有样本计算,训练过程会很慢。从迭代的次数上来看,BGD迭代的次数相对较少。
随机梯度下降法(Stochastic Gradient Descent,SGD)
随机梯度下降法不同于批量梯度下降,随机梯度下降是每次迭代使用一个样本来对参数进行更新。使得训练速度加快。
(1)对目标函数求偏导:
∂ l o s s ( θ ) ∂ θ j = ∂ ∂ θ j 1 2 ∑ i = 1 m ( θ T x ( i ) − y ( i ) ) 2 = ∑ i = 1 m ( θ T x ( i ) − y ( i ) ) x j ( i ) \frac{∂loss(\theta)}{∂\theta_j} = \frac{∂}{∂\theta_j} \frac{1}{2}\sum_{i=1}^m(\theta^Tx^{(i)}-y^{(i)})^2 = \sum_{i=1}^m(\theta^Tx^{(i)}-y^{(i)})x_j^{(i)} ∂θj∂loss(θ)=∂θj∂21i=1∑m(θTx(i)−y(i))2=i=1∑m(θTx(i)−y(i))xj(i)
(2)参数更新:
θ j = θ j − α ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j = \theta_j - \alpha (h_\theta(x^{(i)})-y^{(i)} )x_j^{(i)} θj=θj−α(hθ(x(i))−y(i))xj(i)
优点:
由于不是在全部训练数据上的损失函数,而是在每轮迭代中,随机优化某一条训练数据上的损失函数,这样每一轮参数的更新速度大大加快。
缺点:
- 准确度下降。由于即使在目标函数为强凸函数的情况下,SGD仍旧无法做到线性收敛。
- 可能会收敛到局部最优,由于单个样本并不能代表全体样本的趋势。
- 不易于并行实现。
小批量梯度下降(Mini-Batch Gradient Descent,MBGD)
小批量梯度下降,是对批量梯度下降以及随机梯度下降的一个折中办法。其思想是:每次迭代 使用 b a t c h _ s i z e batch\_size batch_size 个样本来对参数进行更新。
这里我们假设 b a t c h _ s i z e = 10 batch\_size=10 batch_size=10 ,样本数 m = 1000 m=1000 m=1000。
优点:
- 通过矩阵运算,每次在一个batch上优化神经网络参数并不会比单个数据慢太多。
- 每次使用一个batch可以大大减小收敛所需要的迭代次数,同时可以使收敛到的结果更加接近梯度下降的效果。(比如上例中的30W,设置batch_size=100时,需要迭代3000次,远小于SGD的30W次)
- 可实现并行化。
缺点:
b a t c h _ s i z e batch\_size batch_size的不当选择可能会带来一些问题。
逻辑回归
判定边界
逻辑回归是解决分类问题的一个算法,我们可以通过这个算法得到一个映射函数 f : X → y f:X \rightarrow y f:X→y,其中 X X X为特征向量, X = x 0 , x 1 , . . . , x n X = {x_0, x_1, ..., x_n} X=x0,x1,...,xn, y y y为预测结果。在逻辑回归中,标签 y y y是一个离散值。
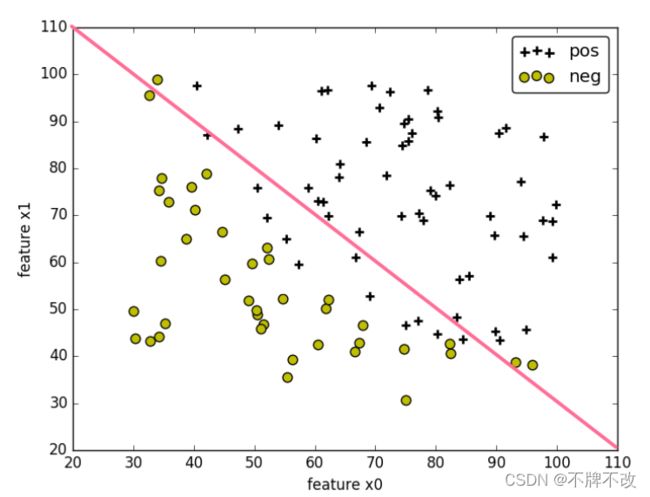
当将训练集的样本以其各个特征为坐标轴在图中进行绘制时,通常可以找到某一个 判定边界 去将样本点进行分类。例如:
线性判定边界:
非线性判定边界:
在图中,样本的标记类型有两种类型,一种为正样本,另一种为负样本,样本的特征 x 0 x_0 x0和 x 1 x_1 x1为坐标轴。根据样本的特征值,可将样本绘制在图上。
在图中,可找到某个判定边界来对不同标签的样本进行划分。根据这个判定边界,我们可以知道哪些样本是正样本,哪些样本为负样本。
因此我们可以通过学习得到一个方程 E θ ( X ) = 0 E_\theta(X)=0 Eθ(X)=0来表示判定边界,即判定边界为 E θ ( X ) = 0 E_\theta(X)=0 Eθ(X)=0的点集。(可以看作是等高超平面)
E θ ( X ) = X T θ E_\theta(X)=X^T\theta Eθ(X)=XTθ
其中 θ = θ 0 , θ 1 , θ 2 , . . . , θ n \theta={\theta_0,\theta_1,\theta_2,...,\theta_n} θ=θ0,θ1,θ2,...,θn,为保留 E θ ( X ) = 0 E_\theta(X)=0 Eθ(X)=0中的常数项,令特征向量 X = 1 , x 1 , x 2 , . . . , x n X={1, x_1, x_2,... , x_n} X=1,x1,x2,...,xn。
为使得我们的边界可以非线性化,对于特征 x i x_i xi可以为特征的高次幂或相互的乘积。
对于位于判定边界上的样本,其特征向量 X X X可使得 E θ ( X ) = 0 E_\theta(X)=0 Eθ(X)=0。因此,判定边界是满足 E θ ( X ) = 0 E_\theta(X)=0 Eθ(X)=0的特征向量 X X X表示的点的集合。
sigmoid函数
在上面,可以通过找到一个判定边界来区别样本的标签,得到一个方程 E θ ( X ) = 0 E_\theta(X)=0 Eθ(X)=0来表示判定边界。
对于二分类问题,即样本标签的类型只有两种类型。
当样本标记的类型只有两种时,其中一类的样本点在判定边界的一边,其会有 E θ ( X ) > 0 E_\theta(X)>0 Eθ(X)>0,而另一类的样本会在判定边界的另一边,会有 E θ ( X ) < 0 E_\theta(X)<0 Eθ(X)<0。
当样本点离判定边界越远时, E θ ( X ) E_\theta(X) Eθ(X)的绝对值越大于 0 0 0,这时样本的标签是某种类型的概率会很大,可能会等于 1 1 1;当样本点离判定边界越近时, E θ ( X ) E_\theta(X) Eθ(X)的接近 0 0 0,样本的标签是某种类型的概率会在 0.5 0.5 0.5左右。
因此,我们可以将 E θ ( X ) E_\theta(X) Eθ(X)函数转换为一种概率函数,通过概率来判断样本的标签是某一种类型的概率会是多少。而这种转换可以使用sigmoid函数来实现︰
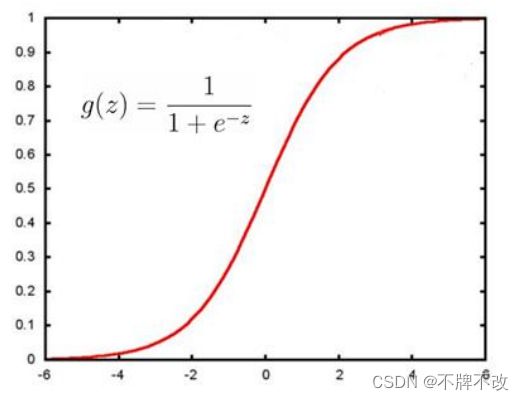
g ( z ) = 1 1 + e − z g(z) = \frac{1}{1+e^{-z}} g(z)=1+e−z1
sigmoid函数图像如下:
从sigmoid函数图像可看出:当z为0左右时,函数值为0.5左右;z越大于0时,函数值越大于0.5越收敛于1;z越小于0时,函数值越小于0.5越收敛于0。
因此,sigmoid函数可适用于在二分类问题中将 E θ ( X ) E_\theta(X) Eθ(X)函数转换为概率函数。
当 E θ ( X ) > 0 E_\theta(X)>0 Eθ(X)>0时,样本标记的类型为某一类型的概率会大于0.5;当 E θ ( X ) ≤ 0 E_\theta(X)≤0 Eθ(X)≤0时,样本标记的类型为某一类型的概率会小于0.5;当 E θ ( X ) E_\theta(X) Eθ(X)约等于0时,样本标记的类型为某一类型的概率会在0.5左右。
在二分类问题中,可以找到逻辑回归函数 h θ ( X ) = s i g m o i d ( E θ ( X ) ) h_\theta(X) = sigmoid(E_\theta(X)) hθ(X)=sigmoid(Eθ(X)),判定边界可看作 h θ ( X ) = 0.5 h_\theta(X)=0.5 hθ(X)=0.5时的等高线。
g ( z ) = 1 1 + e − z h θ ( X ) = g ( E θ ( X ) ) = g ( θ T X ) = 1 1 + e − θ T X g(z) = \frac{1}{1+e^{-z}} \\ h_\theta(X) = g(E_\theta(X)) = g(\theta^TX) = \frac{1}{1+e^{-\theta^TX}} g(z)=1+e−z1hθ(X)=g(Eθ(X))=g(θTX)=1+e−θTX1
不知道你有没有这样的疑问,“ E θ ( X ) E_\theta(X) Eθ(X)不是已经可以确定特征值 X X X属于哪一类了吗,为什么还要映射到sigmoid函数上?这不是多此一举吗?”
如果我们已经知道了参数 θ \theta θ,那么映射到sigmoid函数上以获取类别确实多此一举,但是我们建立模型的时候并不知道 θ \theta θ, θ \theta θ是我们通过训练集训练出来的。要想训练就需要损失函数控制训练的好与坏,损失函数需要连续地表达真实值与预测值之间的差距,因此将离散的两种标签连续化非常重要。sigmoid函数就是将 E θ ( X ) E_\theta(X) Eθ(X)的正负映射成一些连续的函数值,同时还要很好地表达现实含义,即“分为当前类的可能性”。得到连续的值后我们就可以通过特征值与“分为当前类的可能性”之间的函数关系构建损失函数,从而对模型进行训练,得到参数 θ \theta θ。
损失函数
定义
在二分类问题中,若用 h θ ( X ) h_\theta(X) hθ(X) 的值表示正样本的概率,且 h θ ( X ) ∈ ( 0 , 1 ) h_\theta(X) ∈ (0,1) hθ(X)∈(0,1),需要的损失函数应该是这样的:
- 当样本标签的类型是正类型时,若该样本对应的 h θ ( X ) h_\theta(X) hθ(X) 值为1时,即为正类型的概率为 1 1 1,这时损失函数值应为 0 0 0;若该样本对应的 h θ ( X ) h_\theta(X) hθ(X)值为 0.0001 0.0001 0.0001时,即为正样本的概率为 0.0001 0.0001 0.0001,这时候损失函数值应该是一个很大的值。
- 当样本标记的类型是负类型时,若该样本对应的 h θ ( X ) h_\theta(X) hθ(X) 值为0时,即为正样本的概率为 0 0 0,这时损失函数值应为 0 0 0;若该样本对应的 h θ ( X ) h_\theta(X) hθ(X)值为 0.9999 0.9999 0.9999时,即为正样本的概率为 0.9999 0.9999 0.9999,这时候损失函数值应该是一个很大的值。
因此二分类问题中,为满足这种需求,对于单个样本来说,其损失函数可以表示为︰
( h θ ( X ) h_\theta(X) hθ(X) 的值表示正样本的概率)
C o s t ( h θ ( X ) , y ) = { − l o g ( h θ ( X ) ) i f y = 1 − l o g ( 1 − h θ ( X ) ) i f y = 0 Cost(h_\theta(X),y) = \begin{cases} -log(h_\theta(X)) & if & y=1 \\ -log(1-h_\theta(X)) & if & y=0 \end{cases} Cost(hθ(X),y)={−log(hθ(X))−log(1−hθ(X))ifify=1y=0
其中 y = 1 y=1 y=1表示样本为正样本, y = 0 y=0 y=0表示样本为负样本。
结合起来的写法︰
C o s t ( h θ ( X ) , y ) = − [ y l o g ( h θ ( X ) ) − ( 1 − y ) l o g ( 1 − h θ ( X ) ) ] Cost(h_\theta(X),y) = -[\space ylog(h_\theta(X)) - (1-y)log(1-h_\theta(X))\space ] Cost(hθ(X),y)=−[ ylog(hθ(X))−(1−y)log(1−hθ(X)) ]
上式的代价函数也称作:交叉熵代价函数。
对于训练集所有样本来说,共同造成的损失函数的均值 l o s s θ ( X ) loss_\theta(X) lossθ(X)可以表示为︰
l o s s θ ( X ) = 1 m ∑ i = 1 m C o s t ( h θ ( X ( i ) ) , y ( i ) ) loss_\theta(X) = \frac{1}{m} \sum_{i=1}^mCost(h_\theta(X^{(i)}), y^{(i)}) lossθ(X)=m1i=1∑mCost(hθ(X(i)),y(i))
将 C o s t Cost Cost函数代入得:
l o s s θ ( X ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( h θ ( X ( i ) ) ) − ( 1 − y ( i ) ) l o g ( 1 − h θ ( X ( i ) ) ) ] loss_\theta(X) = - \frac{1}{m} \sum_{i=1}^m [\space y^{(i)}log(h_\theta(X^{(i)})) - (1-y^{(i)})log(1-h_\theta(X^{(i)}))\space ] lossθ(X)=−m1i=1∑m[ y(i)log(hθ(X(i)))−(1−y(i))log(1−hθ(X(i))) ]
对于样本来说,其标记 y y y为 1 1 1(正样本)或为 0 0 0(负样本),对于预测概率函数 h θ ( X ) h_\theta(X) hθ(X)来说,预测到样本为正样本的概率值在 0 0 0到 1 1 1之间。
极大似然估计
上面是一种求损失函数的方式,我们也可以换一种方式来求损失函数,即极大似然估计。用极大似然估计来作为损失函数。
如果不知道极大似然:详解最大似然估计(MLE)、最大后验概率估计(MAP),以及贝叶斯公式的理解 - CSDN
上述的损失函数 l o s s θ ( X ) loss_\theta(X) lossθ(X)也可以通过极大似然估计来求得:以 h θ ( X ) h_\theta(X) hθ(X)的值表示正样本的概率,且以 y = 1 y=1 y=1表示正样本, y = 0 y =0 y=0表示负样本,则有:
P ( y = 1 ∣ x ; θ ) = h θ ( x ) P ( y = 0 ∣ x ; θ ) = 1 − h θ ( x ) P(y=1|x;\theta) = h_\theta(x) \\ P(y=0|x;\theta) = 1-h_\theta(x) P(y=1∣x;θ)=hθ(x)P(y=0∣x;θ)=1−hθ(x)
合并上述两个式子则有:
p ( y ∣ x ; θ ) = ( h θ ( x ) ) y ( 1 − h θ ( x ) ) ( 1 − y ) p(y|x;\theta) = (h_\theta(x))^y(1-h_\theta(x))^{(1-y)} p(y∣x;θ)=(hθ(x))y(1−hθ(x))(1−y)
对 m m m个样本,求极大似然估计:
L ( θ ) = ∏ i = 1 m p ( y 1 ∣ x i ; θ ) = ∏ i = 1 m ( h θ ( x i ) ) y i ( 1 − h θ ( x i ) ) ( 1 − y i ) L(\theta) = \prod_{i=1}^mp(y_1|x_i;\theta) \\=\prod_{i=1}^m (h_\theta(x_i))^{y_i}(1-h_\theta(x_i))^{(1-y_i)} L(θ)=i=1∏mp(y1∣xi;θ)=i=1∏m(hθ(xi))yi(1−hθ(xi))(1−yi)
取对数似然估计:
l ( θ ) = l o g L ( θ ) = ∑ i = 1 m y i l o g h θ ( x i ) + ( 1 − y i ) l o g ( 1 − h θ ( x i ) ) h θ ( X ) = 1 1 + e − X T θ l(\theta) = logL(\theta) \\ = \sum_{i=1}^m y_i\space logh_\theta(x_i) + (1-y_i)log(1-h_\theta(x_i)) \\ h_\theta(X) = \frac{1}{1+e^{-X^T\theta}} l(θ)=logL(θ)=i=1∑myi loghθ(xi)+(1−yi)log(1−hθ(xi))hθ(X)=1+e−XTθ1
对数似然取极值(极大值)时的 0 0 0取值便是我们想要的,因此需要对目标函数 l ( θ ) l(\theta) l(θ)进行最大化,即相当于对上述的 l o s s ( θ ) loss(\theta) loss(θ)进行最小化: l ( θ ) = − l o s s ( θ ) l(\theta)=-loss(\theta) l(θ)=−loss(θ)。
梯度下降法求损失函数极小值
损失函数的矩阵法表示:
l o s s ( θ ) = − Y ⋅ l o g h θ ( X ) − ( E − Y ) ⋅ l o g ( E − h θ ( X ) ) loss(\theta) = -Y·logh_\theta(X)-(E-Y)·log(E-h_\theta(X)) loss(θ)=−Y⋅loghθ(X)−(E−Y)⋅log(E−hθ(X))
其中 E E E为单位向量, ⋅ · ⋅ 为内积。
∂ l o s s ∂ θ = − Y ⋅ X T 1 h θ ( X ) h θ ( X ) ( 1 − h θ ( X ) ) + ( E − Y ) ⋅ X T 1 1 − h θ ( X ) h θ ( X ) ( 1 − h θ ( X ) ) \frac{∂loss}{∂\theta} = -Y·X^T\frac{1}{h_\theta(X)}h_\theta(X)(1-h_\theta(X)) + (E-Y)·X^T\frac{1}{1-h_\theta(X)}h_\theta(X)(1-h_\theta(X)) ∂θ∂loss=−Y⋅XThθ(X)1hθ(X)(1−hθ(X))+(E−Y)⋅XT1−hθ(X)1hθ(X)(1−hθ(X))
求导使用了矩阵求导的链式法则,和下面三个公式:
① ∂ l o g X ∂ X = 1 / X \frac{∂logX}{∂X} = 1/X ∂X∂logX=1/X
② ∂ g ( z ) ∂ z = g ( z ) ( 1 − g ( z ) ) ( g ( z ) 为 s i g n m o i d 函 数 ) \frac{∂g(z)}{∂z} = g(z)(1-g(z)) \space \space\space(g(z)为signmoid函数) ∂z∂g(z)=g(z)(1−g(z)) (g(z)为signmoid函数)
③ ∂ X θ ∂ θ = X T \frac{∂X\theta}{∂\theta} = X^T ∂θ∂Xθ=XT
化简后可得:
∂ l o s s ∂ θ = X T ( h θ ( X ) − Y ) \frac{∂loss}{∂\theta} = X^T(h_\theta(X)-Y) ∂θ∂loss=XT(hθ(X)−Y)
在梯度下降法中每一步向量 θ \theta θ的迭代公式如下:
θ = θ − α X T ( h θ ( X ) − Y ) \theta = \theta-\alpha X^T(h_\theta(X)-Y) θ=θ−αXT(hθ(X)−Y)
其中, α \alpha α为梯度下降法的步长。
Softmax Regression
用于解决多元分类问题
前置知识:
① 指数族分布
指数族分布的概率密度函数:
指数族分布其实是一类分布,包括高斯分布、伯努利分布、二项分布、泊松分布、Beta分布、Gamma分布、Dirichlet分布……但它们都能写成统一的形式:
p ( x ) = h ( x ) e θ T T ( x ) − A ( θ ) p(x) = h(x)e^{\theta^TT(x)-A(\theta)} p(x)=h(x)eθTT(x)−A(θ)
分布函数框架中的h(x),η(θ),T(x)和A(θ)并不是任意定义的,每一部分都有其特殊的意义。
- θ \theta θ是自然参数(natural parameter),通常是一个实数
- h ( x ) h(x) h(x)是底层观测值(underlying measure)
- T ( x ) T(x) T(x)是充分统计量(sufficient statistic),能为相应分布提供足够信息的统计量
- A ( θ ) A(θ) A(θ)被称为对数规则化(log normalizer)
② 广义线性模型:广义线性模型到底是个什么鬼? - 搜狐网
Softmax Regression:是对logstic regression扩展的一种多分类器。
详细内容:多分类问题Softmax Regression - CSDN
REF
Logistic Regression(逻辑回归)模型实现二分类和多分类 - CSDN
(img-Dc6GLMQX-1641472243467)]
② 广义线性模型:广义线性模型到底是个什么鬼? - 搜狐网
Softmax Regression:是对logstic regression扩展的一种多分类器。
详细内容:多分类问题Softmax Regression - CSDN