漫画:什么是快速排序?
快速排序是从冒泡排序演变而来的算法,但是比冒泡排序要高效得多,所以叫做快速排序
最好先弄清楚荷兰国旗问题,这样比较好理解
快速排序采用了分治法
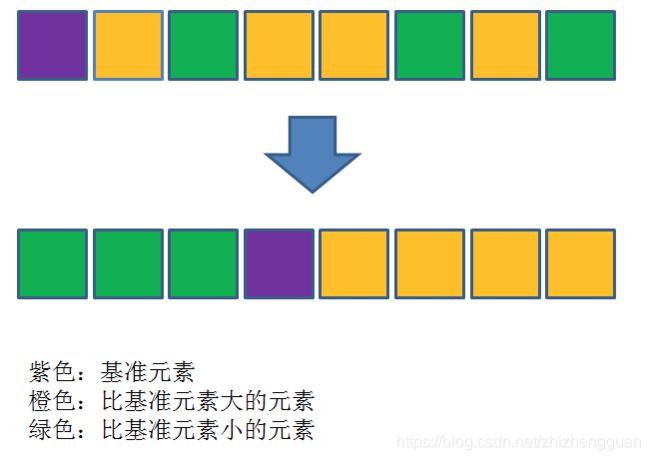
- 同冒泡排序一样,快速排序也属于交换排序,通过元素之间的比较和交换位置来达到排序的目的。
- 不同的是,冒泡排序是在每一轮只把一个元素冒泡的数列的一端,而快速排序在每一轮挑选一个基准元素,并让其他比它大的元素移动到数列的一边,比它小的元素移动到数列的另一边,从而把数列拆解成了两个部分
算法步骤:如果要排序的数组中下标从p到r之间的一组数据,
- 先选择p到r之间的任意一个数据作为 pivot(分区点)。
- 然后遍历p到r之间的数据,
- 将小于pivot的放在左边
- 将大于privot的放在右边
- 将等于pivot的放在中间。
- 经过这一步骤之后,数组p到r之间的数据就被分成了三个部分:
- 前面p到q-1之间都是小于pivot的
- 中间是pivot
- 后面的q+1和r之间都是大于pivot的。
递推公式如下:
递推公式: q u i c k S o r t ( p … r ) = q u i c k S o r t ( p … q − 1 ) + q u i c k S o r t ( q + 1 , r ) 递推公式:quickSort(p…r) = quickSort(p…q-1) + quickSort(q+1, r) 递推公式:quickSort(p…r)=quickSort(p…q−1)+quickSort(q+1,r)
终止条件: p > = r 终止条件:p >= r 终止条件:p>=r
因此,我们可以写出如下代码框架:
// 快速排序,a是数组,n表示数组的大小
void quickSort(int []a, int n){
quickSortInternally(a, 0, n-1);
}
void quickSortInternally(int[] a, int p, int r){
if(p >= r){
return;
}
int q = partition(a, p, r); //获取分区点,对它做荷兰国旗问题
quickSortInternally(a, p, q - 1);
quickSortInternally(a, q + 1, r);
}
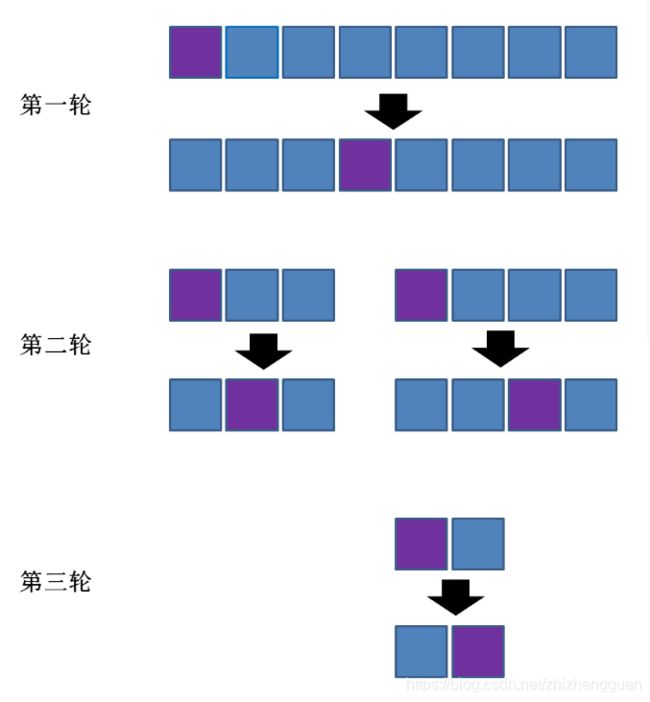
因此我们可以画出如下流程:
- 如图所示,在分治法的思想下,原数列在每一轮被拆分成两部分,每一部分在下一轮又分别被拆分成两部分,直到不可再分为止。
- 这样一共需要多少轮呢?平均情况下需要logn轮,因此快速排序算法的平均时间复杂度是 O(nlogn)。
partition函数
问题是:
- 基准元素是如何选出的?
- 如何把其他元素移动到基准元素的两端?
这两个是快速排序要解决的核心问题,也是partition函数需要时间的核心功能。
这个partition有个专有名词,叫做荷兰国旗问题
基准元素的选择
基准元素,用于在分治过程中以此为中心,把其他元素移动到基准元素的左右两边。
那么基准元素如何选择呢?
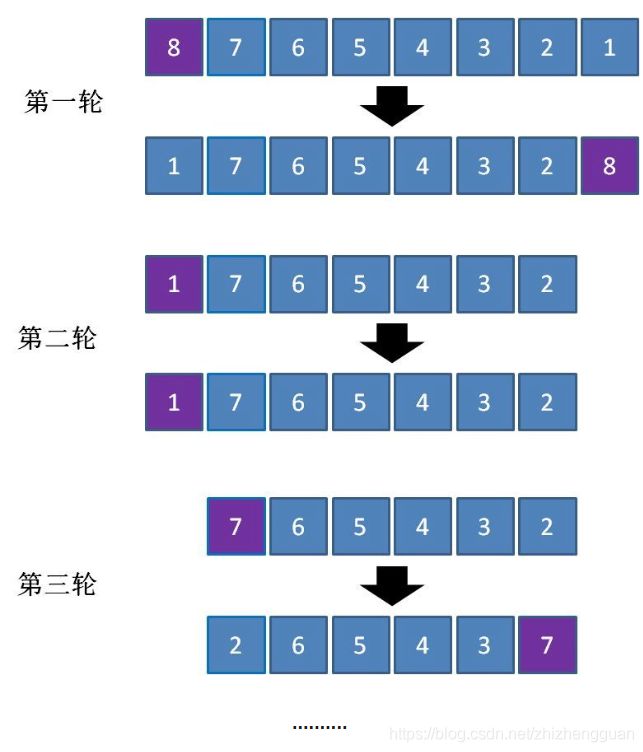
从上面可以看出:
- 整个数列并没有被分成一半一半,每一轮仅仅确定了基准元素的位置
- 这种情况下数列第一个元素要么是最小值,要么是最大值,根本无法发挥分治法的优势
- 此时,快速排序需要进行N轮,时间复杂度退化到了O(N^2)
可以看出,这种O( n 2 n^2 n2)时间复杂度出现的主要原因还是因为分区点选的不管合理,那么分区点应该怎么选择呢?也就是说什么样的分区点才是好分区点呢?
最理想的分区点是:*被分区点分开的两个分区中,数据的数量差不多
如果很粗暴地直接选择第一个或者最后一个数据作为分区点,不考虑数据的特点,肯定会出现之前讲的那样,在某些情况下,排序的最坏情况时间复杂度是 O( n 2 n^2 n2) 。为了提高排序算法的性能,我们也要尽可能地让每次分区都比较平均。
因此,比较常用的分区由两种:
- 三数取中法
- 随机法
随机选择
我们该怎么避免这种情况发生呢?
-
这样一来,即使在数列完全逆序的情况下,也可以有效地将数列分成两部分。
-
当然,即使是随机选择基准元素,每一次也有极小的几率选到数列的最大值或最小值,同样会影响到分治的效果。
这种方法并不能保证每次分区点都选得比较好,但是从概率的角度来看,也不太可能出现每次分区点都选得很差的情况,所以平均角度下,这样选的分区点是比较好的。时间复杂度退化为最糟糕的O( n 2 n^2 n2) 的情况,出现的可能性不大。
三数取中法
我们从区间的首、尾、中间,分别取出一个数,然后对比大小,取这3个数的中间值作为分区点。这样每间隔某个固定的长度,取数据出来比较,将中间值作为分区点的分区算法,肯定要比单纯取一个数据要好。但是,如果要排序的数组比较大,那“三数取中”可能就不够了,可能要“五数取中”或者“十数取中”。
元素的移动
选定了基准元素以后,我们要做的就是把其他元素当中小于基准元素的都移动到基准元素一边,大于基准元素的都移动到基准元素另一边。
如果我们不考虑空间消耗的话,partition()分区函数可以写的非常简单。我们申请两个临时数组X和Y,遍历A[p…r],将小于pivot的元素都拷贝到临时数据X,将大于pivot的元素都拷贝到临时数组Y,最后再将数组X和数据Y中数据顺序拷贝到A[p…r]
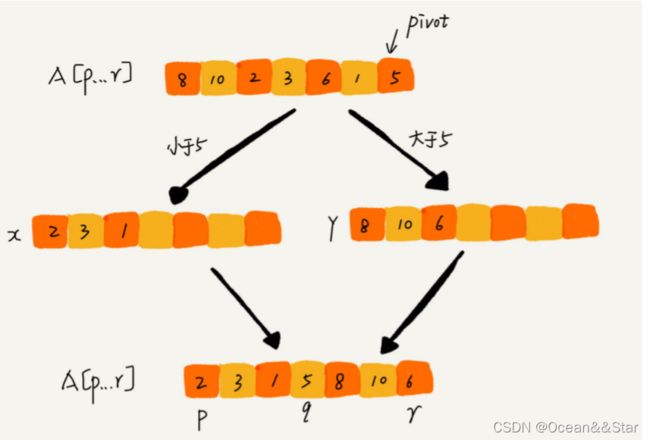
但是,如果按照这种思路实现的话,partition()函数就需要很多额外的内存空间,所以快排就不是原地排序算法了。如果我们希望快排是原地排序算法,那它的空间复杂度就需要是O(1),那 partition() 分区函数就不能占用太多额外的内存空间,我们就需要在 A[p…r] 的原地完成分区操作。
有两种方法:
- 挖坑法
- 指针交换法
指针交换法
// 暂时只实现了将大于基准元素的放到右边
std::vector<int> partition(std::vector<int> &arr, int L, int R, int priv){
int less = L - 1;
int more = R + 1;
int curr = L; // 就是上图的L,当然也可以写成下面那样
while (curr < more){
if(arr[curr] < priv){
std::swap(arr[curr++], arr[++less]);
}else if(arr[curr] > priv){
std::swap(arr[curr] , arr[--more]);
}else{
curr++;
}
}
return { less + 1, more - 1 }; // 和p相等的边界
}
void quickSort(std::vector<int> & arr, int left, int right){
if (arr.size() < 2 ){
return;
}
if (left < right){
int random = left + rand() % (right - left + 1);//在序列中随机选取一个元素
std::swap(arr[left], arr[random]); // 和基准元素交换,这样基准元素就是随机的了
auto mids = partition(arr, left, right, arr[left]);
quickSort(arr, left, mids[0] - 1);
quickSort(arr, mids[1] + 1, right);
}
}
void quickSort(std::vector<int> & arr){
quickSort(arr, 0, arr.size() - 1);
}
还有一种思路:
int partition(std::vector<int> & arr, int p, int r){
int pivot = arr[r];
int i = p;
for(int j = p; j < r; ++j){
if(arr[j] < pivot){
if(i == j){
++i; // 有序区扩大
}else{
std::swap(arr[i], arr[j]);
++i; //有序区扩大
}
}
}
std::swap(arr[i], arr[r]); //处理[基准]
return i;
}
- 我们通过游标i把A[p…r-1]分成两部分。A[p…i-1]的元素都是小于pivot的,我们暂且叫它“已处理区间”,A[i…r-1] 是“未处理区间”。
- 我们每次都从未处理的区间A[i…r-1]中取一个元素A[j],与pivot对比,如果小于pivot,则将其加入到已处理区间的尾部,也就是A[i]的位置。
挖坑法
int partition(std::vector<int> & array, int left, int right){
int pivot = array[left]; // 初始坑
while (left < right){
while (left < right && array[right] > pivot){ //找到右边第一个比基准元素小的元素
right--; // 如果当前正在比较的元素小于等于基准元素,就跳出循环,right就是右边第一个比基准元素小[等于]的索引
}
if (left == right) break; // 如果时因为left == right而跳出循环,那就直接返回
array[left] = array[right]; // 将元素放入坑中, right成为新的坑
while (left < right && array[left] <= pivot){ // 找到左边第一个比基准元素大的元素
left++; // 如果当前正在比较的元素大于基准元素,就跳出循环,left就是左边第一个大于基准元素的索引。
}
if (left == right) break; // 如果时因为left == right而跳出循环,那就直接返回
array[right] = array[left]; // 将元素放入坑中, left成为新的坑
}
// 跳出循环时,一定时因为left = right
array[right] = pivot;
return right;
}
void quickSort(std::vector<int> & arr, int left, int right){
if (arr.size() < 2 ){
return;
}
if (left < right){
int mid = partition(arr, left, right);
quickSort(arr, left, mid - 1);
quickSort(arr, mid + 1, right);
}
}
void quickSort(std::vector<int> & arr){
quickSort(arr, 0, arr.size());
}
因为分区的过程涉及交换操作,如果数组中有两个相同的元素,比如序列 6,8,7,6,3,5,9,4,在经过第一次分区操作之后,两个 6 的相对先后顺序就会改变。所以,快速排序并不是一个稳定的排序算法。
性能分析
(1)快排的时间复杂度
快排也是用递归实现的。如果每次分区操作,都能正好的把数组分成大小接近的两个小区间,那快排的时间复杂度递推求解公式跟归并是相同的。所以,快排的时间复杂度也是 O(nlogn)。
T ( 1 ) = C ; n = 1 时,只需要常量级的执行时间,所以表示为 C 。 T(1) = C; n=1 时,只需要常量级的执行时间,所以表示为 C。 T(1)=C;n=1时,只需要常量级的执行时间,所以表示为C。
T ( n ) = 2 ∗ T ( n / 2 ) + n ; n > 1 T(n) = 2*T(n/2) + n; n>1 T(n)=2∗T(n/2)+n;n>1
但是公式成立的前提是每次分区操作,我们选择的pivot都很合适,正好能将大区间对等的一分为二。但实际上这种情况是很难实现的。
举一个比较极端的例子,如果数组中的数据原来就是已经有序的了,比如1、3、5、6、8,如果我们每次选择最后一个元素作为pivot,那每次分区得到的两个区间但是不均等的,我们需要进行大约n次分区操作,才能完成快排的整个过程。每次分区我们平均要扫描大约 n/2 个元素,这种情况下,快排的时间复杂度就从 O(nlogn) 退化成了 O( n 2 n^2 n2)。
我们刚刚讲了两个极端情况下的时间复杂度,一个是分区极其均衡,一个是分区极其不均衡。它们分别对应快排的最好情况时间复杂度和最坏情况时间复杂度。那快排的平均情况时间复杂度是多少呢?
T(n) 在大部分情况下的时间复杂度都可以做到O(nlogn),只有在极端情况下,才会退化到 O( n 2 n^2 n2)。而且,我们也有很多方法将这个概率降到很低
所以,快速排序的平均时间复杂度是 O(nlogn),最坏情况下的时间复杂度是 O(n^2)。
快排 VS 归并
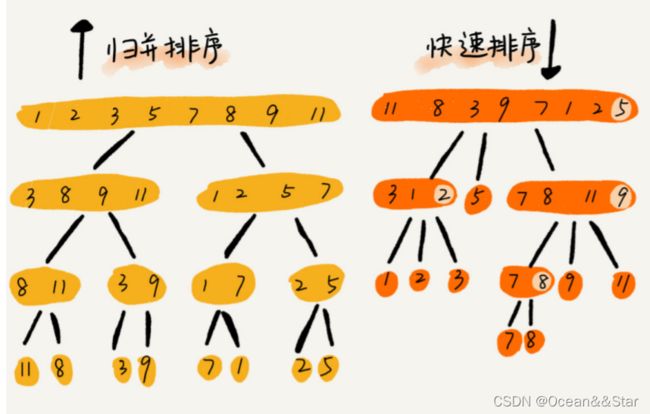
问题:快排和归并用的都是分治思想,递推公式和递归代码也非常相似,那它们的区别在哪里呢?
可以发现,归并排序的处理过程是由下到上的,先处理子问题,然后在合并。而快排的处理过程是由上到下的,先分区,然后再处理子问题。归并排序虽然是稳定的、时间复杂度为O(nlogn)的排序算法,但是是非原地排序算法。归并之所以是非原地排序算法,主要原因是合并函数无法在原地执行。快排通过设计巧妙的原地分区函数,可以实现原地排序,解决了归并排序占用太多内存的问题
因此:
- 归并排序算法是一种在任何情况下时间复杂度都比较稳定的排序算法,这也使它存在致命的缺点,即归并排序不是原地排序算法,空间复杂度比较高,是 O(n)。正因为此,它也没有快排应用广泛。
- 快速排序算法虽然最坏情况下的时间复杂度是 O ( n 2 ) O(n^2) O(n2),但是平均情况下时间复杂度都是O(nlogn)。不仅如此,快速排序算法时间复杂度退化到 O ( n 2 ) O(n^2) O(n2)的概率非常小,我们可以通过合理地选择 pivot 来避免这种情况。
底层的排序方法
几乎所有的编程语言都会提供排序函数,比如C语言中的qsort()、C++ STL中的sort()、stable_sort(),还有 Java 语言中的Collections.sort()。在平时的开发中,我们也都是直接使用这些现成的函数来实现业务逻辑中的排序工具,那这些函数是如何实现的呢?底层都利用了哪种排序算法,应该如何实现一个通用的、高性能的排序函数呢?
第一个要解决的问题是:如果要实现一个通用的、高效率的排序函数,我们应该选择哪种排序算法?
- 线性排序算法的时间复杂度虽然比较低,但是适用场景比较特殊。所以如果要写一个通用的排序函数,不能选择线性排序算法。
- 如果对小规模的数据进行排序,可以选择时间复杂度为O( n 2 n^2 n2)的算法;如果对大规模数据进行排序,时间复杂度是 O(nlogn) 的算法更加高效。所以,为了兼顾任意规模数据的排序,一般都会首选时间复杂度是 O(nlogn) 的排序算法来实现排序函数。
- 时间复杂度是 O(nlogn) 的排序算法不止一个,比如归并排序、快速排序、堆排序等。堆排序和快排有比较多的应用,比如Java语言采用堆排序实现排序函数,C语言使用快排实现排序函数。但是归并排序用的并不多
- 我们知道,快排在最坏情况下的时间复杂度是O( n 2 n^2 n2),而归并排序可以做到平均情况、最坏情况下的时间复杂度都是O(nlogn),从这点上看起来很诱人,那为什么它还是没能得到“宠信”呢?这是因为归并排序并不是原地排序算法,空间复杂度是O(n)。所以,粗略点、夸张点讲,如果要排序 100MB 的数据,除了数据本身占用的内存之外,排序算法还要额外再占用 100MB 的内存空间,空间耗费就翻倍了。
因此,快排比较合适用来实现排序函数。但是,快排在最坏情况下的时间复杂度是O( n 2 n^2 n2),如何解决这个“复杂度恶化”的问题呢?随机选择基准点或者多路取中法
以拿 Glibc 中的 qsort() 函数分析举例
- qsort()会优先使用归并排序来排序输入数据,因为归并排序的空间复杂度是O(n),所以对于小数据量的排序,比如1KB、2KB等,归并排序额外需要1KB、2KB 的内存空间,这个问题不大。现在计算机的内存都挺大的,我们很多时候追求的是速度。
- 当要排序的数据量比较大的时候,qsort() 会改为用快速排序算法来排序。那 qsort() 是如何选择快速排序算法的分区点的呢?选择分区点的方法就是“三数取中法”
- 对于递归太深会导致堆栈溢出的问题,qsort()是通过自己实现一个堆上的栈,手动模拟递归来解决的
- 另外,qsort()并不仅仅用到了归并排序和快速排序,它还用到了插入排序。在快速排序的过程中,当要排序的区间中,元素的个数小于等于4时,qsort()就会退化为插入排序,不再用递归来做快速排序,因为O( n 2 n^2 n2) 时间复杂度的算法并不一定比O(nlogn)的算法执行时间长。
- 在 qsort() 插入排序的算法实现中,也利用了哨兵这种编程技巧。虽然哨兵可能只是少做一次判断,但是毕竟排序函数是非常常用、非常基础的函数,性能的优化要做到极致。
为什么O( n 2 n^2 n2) 时间复杂度的算法并不一定比O(nlogn)的算法执行时间长呢?
- 虽然算法的性能可以通过时间复杂度来分析,但是,这种复杂度分析是比较偏理论的,如果我们深究的话,实际上时间复杂度并不等于代码实际的运行时间。
- 时间复杂度代表的是一个增长趋势,如果画成增长曲线图,你会发现 O( n 2 n^2 n2) 比 O(nlogn) 要陡峭,也就是说增长趋势要更猛一些。但是,我们前面讲过,在大 O 复杂度表示法中,我们会省略低阶、系数和常数,也就是说,O(nlogn) 在没有省略低阶、系数、常数之前可能是 O(knlogn + c),而且 k 和 c 有可能还是一个比较大的数。
- 当我们对小规模数据(比如 n=100)排序时, n 2 n^2 n2的值实际上比knlogn+c 还要小。
- 所以,对于小规模数据的排序,O( n 2 n^2 n2) 的排序算法并不一定比 O(nlogn) 排序算法执行的时间长。对于小数据量的排序,我们选择比较简单、不需要递归的插入排序算法。
golang实现
package main
import (
"fmt"
"math/rand"
"time"
)
func QuickSort(arr[] int)[]int{
length := len(arr)
if length <= 1{
return arr
}else{
base := arr[0] // 第一个作为基准
low := make([]int, 0) //存储比我小的
mid := make([]int, 0) //存储与我相等
high := make([]int, 0) //存储比我大的
for i := 0; i < length ; i++ {
if arr[i] < base {
low = append(low, arr[i])
}else if arr[i] == base {
mid = append(mid, arr[i])
}else{
high = append(high, arr[i])
}
}
low, high = QuickSort(low), QuickSort(high)
return append(append(low, mid...), high...)
}
}
func QuickSortRandom(arr[] int)[]int{
length := len(arr)
if length <= 1{
return arr
}else{
rand.Seed(time.Now().UnixNano())
base := arr[rand.Intn(length)] // 随机基准
low := make([]int, 0)
mid := make([]int, 0)
high := make([]int, 0)
for i := 0; i < length ; i++ {
if arr[i] < base {
low = append(low, arr[i])
}else if arr[i] == base {
mid = append(mid, arr[i])
}else{
high = append(high, arr[i])
}
}
low, high = QuickSort(low), QuickSort(high)
return append(append(low, mid...), high...)
}
}
func main() {
arr := []int{13,14,94,33,82,25,59,94,65,23,45,27,73,25,39,10, 11, 13, 13, 13}
fmt.Println(QuickSortRandom(arr))
fmt.Println(arr)
}