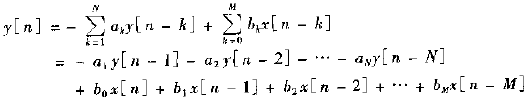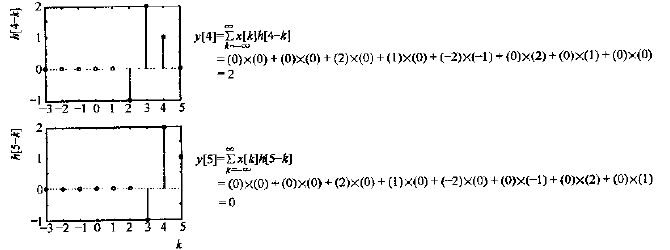数字信号处理－chap3 滤波、差分方程、卷积

１.滤波

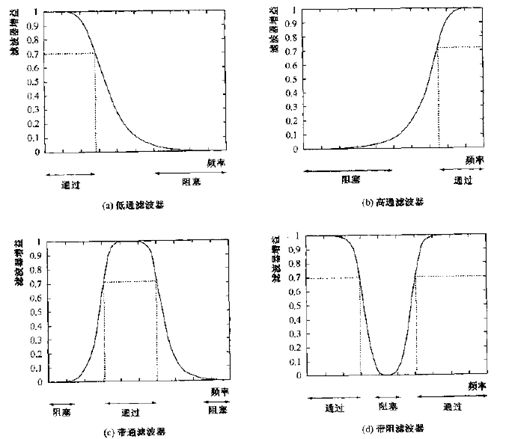
滤波器以特定方式改变信号的频率特性，从而改变信号。

高通滤波器滤除低频信号，强化信号的锐变。

 

2.线性、时不变、因果系统

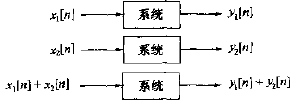
线性系统满足叠加原理

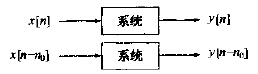
时不变系统的输入延迟，则输出也延迟相同量

因果系统的输出取决于现在和以前的数据，与未来的数据无关。

3.差分方程

差分方程可用于描述线性、时不变、因果数字滤波器。其表达式如下，

写为下面形式更清晰

其中 为滤波器系数，决定了每个输入和输出对第n个输出的贡献。它清晰的说明了每个新的输出y[n]是如何受过去的输出、现在的输入和过去的输入影响的。

递归滤波器：依赖于输入和过去的输出。

非递归滤波器：仅依赖于输入。

4.脉冲响应

由于所有的数字信号都可以由脉冲函数构成 ，所以脉冲响应可用来求各种输入的输出（响应）。因此说，脉冲响应反映了滤波器的基本特性。差分方程可以计算滤波器的脉冲响应。

无限脉冲响应(infinite impulse response IIR)：对于递归滤波器，因为新的输入取决于过去的输出和输入，因此即使某个点以后没有输入，其脉冲响应也仅会越来越小，绝不会下降到零。

有限脉冲响应(infinite impulse response IIR)：对于非递归滤波器，因为新的输入仅取决于输入，因此当某个点以后没有输入，其脉冲响应会逐步下降到零。

当输入是脉冲函数时，只有输入中的单个脉冲到达过去的M点之前，非递归滤波器的输出才能受到脉冲输入的影响，此后滤波器的输入为零，有下式

       （1）

对于非递归滤波器，脉冲响应的采样值给出了差分方程的系数

由              （2）

则其脉冲响应为

                  （3）

由（1）＝（2）得                 （4）

则（4）带入（2）得

   （4）

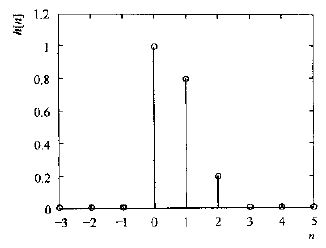
例：写出下图所示脉冲响应的滤波器差分方程

 

5.卷积

卷积提供了差分方程之外的另一种滤波器实现方法。

要理解卷积，首先将信号表示为脉冲函数之和。每个脉冲函数 的输出为脉冲响应 ，采样值为每个脉冲函数提供了权系数。因此由全部输入引起的 是这些脉冲响应的加权和

                             （5）

注：公式（5）和（4）是等价的，由此可看出卷积与差分方程间的关系。

同时，也可知数字系统的输出是输入与其脉冲响应的卷积，如下图所示

5.1 数字卷积的计算

计算步骤

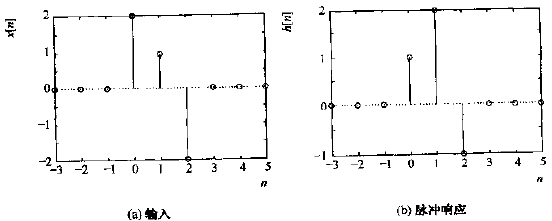
例子：数字系统的输入x[n]和脉冲响应h[n]如下图所示，求系统输出y[n]

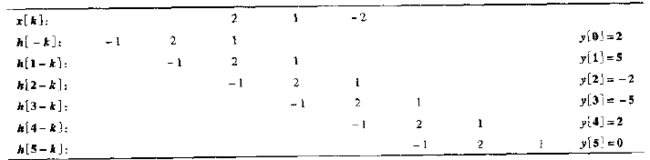
计算过程的图形表示

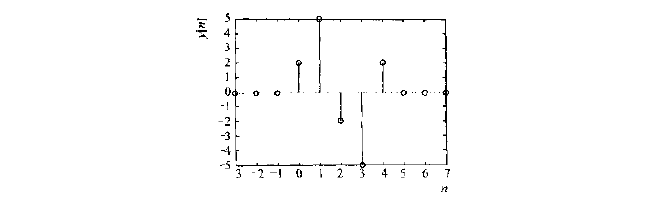
系统输出

计算过程的列表表示

5.2 边界效应

当输入序列的前后均为零（如前面例子所示），那么计算的输出具有物理意义。但很多情况下，采样开始前的输入未知，当脉冲响应与未知的输入采样重叠时，由于实际的输出值可能受到采样开始前输入信号的影响，所以无法准确计算。计算的开始和末尾都可能存在这种线性，称为边界效应（boundary effect）。

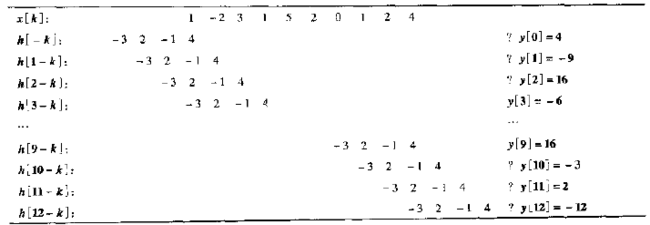
下面例子中，输入序列长度为10，脉冲响应长度为4。当脉冲响应采样点部分位于输入信号采样值之外时，输出就不确定（表中以？标识）。解决边界效应有许多方法，包括给输入信号补零、重复边缘值、对整个输入信号进行周期延拓。

6.差分方程与卷积

滤波器的差分方程     （1）

数字卷积的公式                 （2-a）

                 或                  （2-b）

对于非递归系统，式（1）和（2）都可以描述它。不同之处在于，（1）需要滤波系数，（2）需要脉冲响应h[k]。

对于IIR系统，有无穷多个h[n]。由下例可见对于IIR滤波器由于其脉冲响应有无穷个非零项，用差分方程好一些。

对于FIR系统，h[n]的长度有限。由下例可见，FIR滤波器的脉冲响应仅有有限个非零采样值，所以卷积和差分运算都适用。