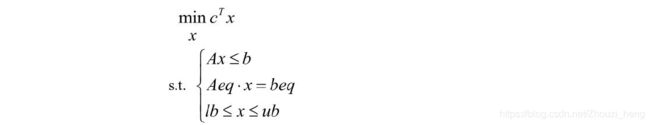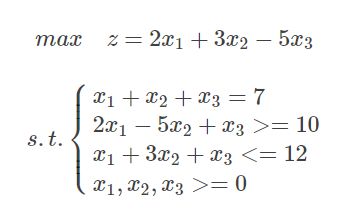数学建模(一):LP 问题
文章目录
- 数学建模(一):LP 问题
-
- 一、 MATLAB求解
- 二、 Python 求解
数学建模(一):LP 问题
在人们的生产实践中,经常会遇到如何利用现有资源来安排生产,以取得最大经济效益的问题。此类问题构成了运筹学的一个重要分支—数学规划,而线性规划(Linear Programming 简记LP)则是数学规划的一个重要分支。自从1947年G.B.Dantzig提出求解线性规划的单纯形方法以来,线性规划在理论上趋向成熟,在实用中日益广泛与深入。特别是在计算机能处理成千上万个约束条件和决策变量的线性规划问题之后,线性规划的适用领域更为广泛了,已成为现代管理中经常采用的基本方法之一。
我们可以使用 lingo 来求解复杂的线性规划问题:https://blog.csdn.net/qq_62789540/article/details/125926169,这里的重点不是 lingo
一、 MATLAB求解
线性规划求解主要弄清楚两个部分,目标函数(max,min)和约束条件(s.t.),我们求解时一般要化为MATLAB标准形式:
其中 c 和 x 为 n 维列向量,A、Aeq为适当维数的矩阵,b、beq为适当维数的列向量。
注意,是求最小值,而不是最大值。
如果使用MATLAB求解的代码为:
[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
%% LB,UB分别为x的上界和下界,即最优解的范围
如,求解:
代码示例:
c = [-2, -3, 5]; % 将最大值装换为求最小值
A = [
[-2, 5, -1];
[1, 3, 1]
]; % Ax <= b
b = [-10; 12];
Aeq = [1, 1, 1]; % Aeq x = beq
beq = 7;
[x,y] = linprog(c, A, b, Aeq, beq, zeros(3, 1));
x, y = -y % 最后记得要把最终解加一个负号,装换为最大值
二、 Python 求解
使用 Python 求解的话,需要 numpy 和 scipy 库的支持。
第三方库的安装:pip install numpy, scipy -i https://mirrors.aliyun.com/pypi/simple
from scipy import optimize
import numpy as np
#求解函数
res = optimize.linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
#目标函数最小值
print(res.fun)
#最优解
print(res.x)
我们还是求解上述的那个线性规划问题:
示例代码:
from numpy import array, zeros
from scipy import optimize
c = [-2, -3, 5]
A = [
[-2, 5, -1],
[1, 3, 1]
]
b = [
[-10],
[12]
]
Aeq = [[1, 1, 1]]
beq = [7]
res = optimize.linprog(array(c), array(A), array(b), array(Aeq), array(beq), (0, None))
print(-res.fun, res.x)
fun就是目标函数最小值,x就是最优解。
当然,我们也可以使用 lingo 来求解线性规划的问题。