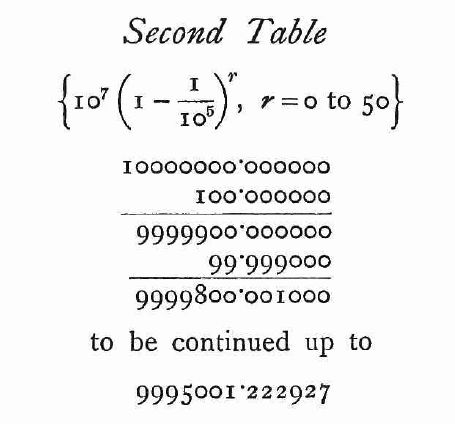理解对数——Napier和导数的发明(1614年)

Napier和他在1614年发明的对数

(JOHN NAPIER AND THEINVENTION OF LOGARITHAMS 1614)

E.W.Hobson (Ernest William Hobson)

今年(译注：作者E.W.Hobson做报告的时间)将在爱丁堡皇家学会(the Royal Society of Edinburgh)的赞助(auspices)下举行庆祝活动(celebration)，以纪念科学史上最伟大事件之一的John Napier的“Mirifici Logarithmorum CanonisDescriptio”(奇妙的对数法则说明书)出版的三百周年纪念(tercentenary)，这部书体现了世界上最伟大的科学发现之一的作品。对数的发明，不仅标志着数学科学中最重要的一个进步，而且为所有需要进行巨量数值计算的人们提供了一种省力的重要工具，它的重要性只有印度发明的伟大的计数系统可以与之相提并论。

详细研究一项伟大发现或发明由其创始人(originator)提出的形式，并详细追溯与该发现相关的基本思想在他的脑海中形成的模式，几乎总是非常具有启发性的(instructive)，即使是因为后来的发展或简化可能已经改变了发明之初的底层原理(更重要的是改变了其实践方法)，我们已经习惯于(至少在表面上)从一个与原来的发现者之某一视角完全不同的角度来看待这个问题，这种回顾也显得很有必要。对数的情况远非是这条法则的例外；因此(accordingly)，我打算尽可能简洁地说明Napier头脑中的对数概念，以及他实际构建对数表的方法。

为了充分理解天才(genius)John Napier所完成的任务的艰巨性，要认识到在17世纪早期，在这个微积分发明之前的时代，当时还没有发明通过无穷级数进行计算的方法，可用于表的计算的手段非常有限，这就要求有一些想象力。Napier的对数概念涉及对某种函数关系的性质和结果的完全清楚的理解，当时数学家的头脑中还没有制定或存在这种关系的一般概念，并且还处于René Descartes(笛卡尔)在本世纪后期发明坐标几何这一伟大发明来直观地阐明这种函数关系之前。 现代数学家将对数函数视为指数函数的逆函数； 可能在我们看来，由于我们都熟悉涉及指数(indices)的运算，所以对数的概念在那种逆函数关联中会以相当明显的方式出现。然而，我们必须记住，在Napier的时代，指数的概念，就其普遍性而言，并不是数学家数学思想储备的一部分，而且还没有使用指数记法(exponentialnotation)。

1. Napier的生平简介(summary of the life of Napier)

我必须满足于对Napier生平的外在事实做一个极其简短的描述(对Napier的生平和活动的完整介绍，可参见Mark Napier所著的著作<>( Merchiston的John Napier回忆录)，出版于1834年)。

John Napier(Napier这个名字有各种拼写形式，John Napier采用了几种写法，因为我们发现的拼法就有Napeir，Nepair，Nepeir，Neper，Nepper，Naper，Napare，Naipper 这几种)是Merchiston的第八代Napeir，通常被称为Merchiston的男爵(Baron)，或恐惧，于1550 年出生在爱丁堡附(Edinburgh)近的Merchiston，当时他的父亲Archibald Napier只有16岁多一点。John Napier于1563年被圣安德鲁斯大学(St Andrews)录取(matriculated)，但没有在那里呆足够毕业和时间，因为他在1566年之前离开，前往欧洲大陆继续他的学业，并于1571年或之前回到Merchiston。他的第一次婚姻，生了他的儿Archibald，此子于1627年被擢升为贵族(peerage)，成为Napier勋爵(Lord)，还于1572生了一个女儿。他的妻子于1579年去世几年后，他又结婚了。他的第二次婚姻生了5个儿子和5个女儿；他的二儿子做他的图书馆管理员。1588年西班牙无敌舰队(Spanish Armada)的入侵导致Napier成为了一名狂热的新教徒(ardent Protestant)，在教会政治中发挥了相当大的作用。大约在1593年1月到1594年1月期间，他出版了他的第一部著作<>(对整个圣约翰启示录的简单发现)。这本书被认为在苏格兰神学文学(theological literature)史上具有相当重要的意义，因为它包含了一种远远超前于那个时代的解释方法；它使用了包括英语、法语、德语和荷兰语在内的多种语言版本进行传播。

1594年7月，Napier与刚被取缔的暴躁男爵(turbulentbaron) Restalrig的Robert Logan签订了一份奇怪的合同。在这份似乎表明John Napier并未摆脱对魔法的普遍信仰的合同中，他同意努力发现本应隐藏在Logan住所(dwellingplace) Fast Castle 中的宝藏。Napier在发现宝藏后将获得三分之一的宝藏，考虑到“the said Jhone sail do hisutter & exact diligens to serche & sik out, and be al craft &ingyne that he dow, to tempt, trye, and find out the sam, and be the grace ofGod, atiier sail find the sam, or than mak it suir that na sik thing hes beenthair; sa far as his utter trawell diligens and ingyne may reach(这位Jhone航海家竭尽全力去搜索和寻找，并且是他所追求、诱惑、尝试和追求的精湛技艺”找出山姆，并成为上帝的恩典，在航行中找到山姆，或者让他认为那是他曾经做过的事情是合适的；只要他的努力和英格尼所能达到的极限)。”

在一份日期为1596年6月7日的文件中，Napier描述了他所做的一些神秘的发明，这些发明“在论文的日子里，对于保卫这只手和抵御上帝真理和宗教的陌生敌人是有益的和必要的。” 他在这个方向上的活动无疑是受到了普遍预期的西班牙菲利普入侵的恐惧的刺激。值得注意的是，考虑到他的许多后代的军事品味。这些发明包括一面可以在任何距离上燃烧敌人船只的镜子，一种能够摧毁圆弧周围一切的大炮，以及一辆圆形金属战车,其构造使得它的居住者可以快速轻松地移动它，同时通过它上的小孔发射。Napier的实际思维也体现在他对农业的关注中，特别是在Merchiston庄园(estate)，那里的土地通过一个带盐的施肥系统进行耕作。

有证据表明，数学从小就吸引了Napier的注意力。从一本书名为<>(物流艺术)(于1839年首次出版)的数学书中(译注：原书中为“MS.”，没有说明指的是什么，猜测应该为“Mathematics”的缩写)，似乎表明他对算术和代数的研究使他开始考虑方程的虚根(imaginaryroots)，并酝酿提取方程所有次数的根的通用方法。但是，可能由于时代环境的影响，导致他将这一项研究工作搁置在一边，而致力于去探索消除涉及数值计算的费时劳动力的方法。在16世纪下半叶，大陆的数学家们花费了巨大的精力在自然三角函数的计算表方面。这方面最著名是数学家 Georg Joachim Rheticus，这项伟大的计算，它的工作(在对数发明前)从未被取代(superseded)，其工作的最终成果体现在(embodied)每10秒计算出精确到小数点后15位的自然正弦表中，这项成果由Pitiscus发表于1613年，也就是Napier发表对数发现的前一年，对数的发现注定要彻底改变所有计算方法，并用对数代替自然三角函数的使用。17世纪初，Johannes Kepler(开普勒)从事一项艰巨的任务，即发现并通过数值计算验证行星的运动定律。在这个数字计算的时代，Napier忙于发明减少其中所涉及劳动的方法。他自己在他的“Rabdologia(筹算)”中指出，对数是“a me longo tempore elaboratum(我长期开发出来的)”一种简化计算的法则(canon)。从出自Kepler的一封信可以看出，一位苏格兰人，可能是Napier家族的朋友Thomas Craig，在1594 年向天文学家Tycho Brahe表示，有希望实现算术过程的重大简化。有强有力的证据表明，Napier在方法发两点20年前就将他这种可能的希望传达给了Craig。

“Descriptio(说明书)”， 正如随后对其进行的解释那样，在1614年正式发布时一开始就说明了这一点——“说明书”。大约在同一时间，Napier设计了几种机械辅助工具来执行乘法和除法以及计算平方根和立方根。1617年，他在他的“Rabdologia(筹算)(筹:泛指计数的用具)”中发布了对这些发明的说明，正如他所说，“为了那些可能更喜欢使用自然数的人。”Napier称之为“筹算”的方法通过一组计算杆(a set of rods)，通常称为“Napier(乘法)骨筹(木质、金属、硬纸板)(Napier's bones)”来实现的乘法和除法的计算组成，1617年，在“筹算”发布后，Napier去世了。

“说明书”并没有包含构造这种“绝妙法则”的方法的说明。在书中第11章末尾的“Admonitio(提醒)”中，Napier解释说，他更愿意在发表构造方法之前等待学术界发表对法则的意见；他说：“因为我希望出现博学之士的判断和谴责，在其他内容草率发表之前，先暴露给嫉妒者们诽谤。”

“Mirifici Logarithmorum CanonisConstructio(典型对数的奇妙构造)”中包含对构造绝妙法则的构造方法的完整解释，以及对Napier对数理论的清晰说明，由他的儿子Robert Napier于1619年出版。Robert Napier在序言中指出，说这部作品是他父亲在“对数(logarithm)”这个词被发明之前几年写的，因此比“说明书”出版的日期更早。后者通篇使用“对数”一词，但在“构造”中，除标题外，对数(logarithm)称为“numeri artificiales(artificial numbers)”(译注：“人工数”或“人造数”，即相对于“自然数”而言，是人为构造的数)。在解释说作者没有对这部小论文进行最后润色之后，编辑(即RobertNapier)写道：“我也不怀疑，如果上帝给予更长时间的享受，这部作者去世后的作品会以更加完美且完成的状态呈现。作者的生命，我最亲爱的父亲，最聪明的人认为，在他身上，除了其他杰出的天赋外，他还表现出卓越的才能，即最困难的事情都可以通过一种可靠而简单的方法来解决(unravelled)，以及用最少言辞来表述。”

2. 当代数学家对(对数)法则的接受(Reception of the Canon by Contemporary Mathematicians)

这项新发明迅速引起了英国和外国数学家的注意，考虑到当时的情况，这可能会让我们大吃一惊。特别是个绝妙法则的发布受到了Kepler的热烈欢迎。Kepler在他1620年的“星历表(Ephemeris)”中，他发布了一封于1619年7月28日写给Napier的信作为献词，热烈祝贺他的发明以及他给天文学带来的好处。Kepler解释了他是如何验证法则的，除了在象限(quadrant)开始附近的一些不准确之外，没有发现其中的本质错误。这封信是在Napier去世两年后写的，Napier并没有听说过为封信。1624年，Kepler本人发表了Napier对数表，并进行了修改和补充。“说明书”一书于1614年出版后，立即引起了Henry Briggs(1556-1630年)的注意，Henry Briggs是剑桥大学圣约翰学院的院士(Fellow)，伦敦金融城的格雷欣(Gresham)几何学教授，后来又是牛津大学的萨维尔(Savilian)几何学教授，作为Napier 的继任者，他以改进形式构造对数表，这项工作我将在后面提到。在日期为Gresham House，1615年3月10日，写给大主教Ussher(Archbishop Ussher)的信中，Briggs写道：“Napper，Markinston 领主，已经用他令人钦佩的新对数让我的头和手开始工作。如果可以让上帝高兴的话，我希望今年夏天见到他，因为我从来没有见过比这本书更让我高兴，或者让我更加好奇的书。”Briggs拜访了Napier，并在1615年和他待了一个月，1616年再次拜访了他，如果纳皮尔的生命得以幸免，他打算在1617年再次拜访他。另一位著名的英国数学家EdwardWright，他是冈维尔(Gonville)与凯斯(Caius)学院的教授，他立刻看到了对数在航海方面的重要性，在航海史上他占据了显着的位置，翻译了“说明书”(译注：从其书名可以看出，大概Napier的“说明书”这部书是用拉丁语写的，Wright将其译为英语版出版)，但他在其译本出版前于1615年去世。然而，该译本于1618年由他的儿子Samuel Wright出版。

3.“说明书”一书的内容及对数构造方法(contents of the " Descriptio " and of the "Constructio")

“说明书”一书由一个修饰性(ornamental)标题页、57页解释性内容和90页表组成。此处复制了表格的样本页(specimen)(如下图1)。解释性内容包含对Napier的对数概念、对数的主要性质以及它们在平面(plane)和球面(spherical)三角形求解中的应用的说明。此处给出了Napier著名的圆形部件法则(rules of circular parts)，其中包含解决直角球面三角形的完整公式系统。表中给出的对数是从0°到90°角度的正弦值，间距为1分(译注：1分等于60分之一度)，给到七至八位数字。该表按半象限排列，因此角度的正弦对数和余弦对数出现在同一条线上，它们的差在微分表中给出，从而形成对数正切表。必须记住，在那个时代及之后很长一段时间内，角的正弦并不像现在那样被视为比率，而是被视为给定半径的圆的某一圆心角正对的半弦(即圆心角对应的弦的一半)的长度(即，以长度度量正弦，而不是以比率度量正弦)。Napier取半径为个单位(units),因此，90°的正弦称为满正弦(whole sine)(圆心角为180°时其弦长等于直径，弦的一半就是半径)；越小的角的正弦从这个值向0方向递减。因此，这个表的刻录的数是从0到之间的数的对数之一，不是等距数(equidistant numbers)，而是对应于等距角。有一点非常重要，即，应注意到，Napier表中的对数并不是我们现在所知的Napier对数或自然对数(以e为底的对数)。

Napier对数字e的存在没有明确的认识，也不知道对数系统底数的概念，尽管正如我们将要看到的那样，他完全知道可能的对数系统中的任意元素。他的选择是为了使0°和 90° 之间的角度的正弦的对数，即0和之间的数，正数，以便囊括相当大的整数部分。

---------------------------图1 Napier对数表的样本副本------------------------

“构造”由两页序言和57页正文组成。此处清楚地解释了对数的概念，并详细说明了实际构建法则的连续步骤。在这项工作中，给出了用文字表达的球面三角形解的四个公式之一，称为Napier类比(Napieranalogies)；其他三个公式后来由Briggs添加，很容易从Napier 的结果中推导出来。

4. 小数点(the decimal point)

我们目前的小数点表示法似乎是由Napier独立发明的，尽管据说JobstBiirgi 更早地使用了点或半括号，目的是将小数位与整数部分数字分开(注：Pitiscus在1612年出版的“三角函数”的最新版本的附录中也使用了小数点。)。

小数的发明归功于Simon Stevin(1548-1620)，他于1585年用荷兰语出版了一本小册子“DeThiende(论十进制)”，同年又用法语出版了一本名为“LaDisme(十进制算术)”的小册子，其中引入了小数分数系统，并在其中推荐了度量衡和货币的十进制系统。在“筹算”中，Napier在“Admonitio pro DecimaliArithmetica(小数运算提示)”中提到了Stevin，他强调了使用小数所产生的简化，并引入了带小数点的符号。例如，按照Stevin以及其他相关人们的思想，用记法

来替代Napier的记法94•1305 。稍后一些时候，Briggs有时候采用记法941305。很显然，Napier引入的小数点的记法，虽然直到18世纪才被普遍采纳，但是远远优于Stevin和后来的写作者提出来的更复杂的记法，更能适应与算术相关的数的完整整数部分和小数部分，并强调小数系统(decimal fractions)仅涉及我们的符号系统针对整数的基本概念的扩展，即与小数位(decimal scale)相关的数字值完全取决于其位置。

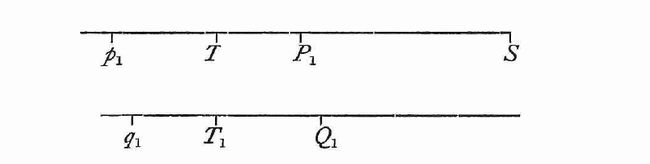
Napier假设了一条直线TS(图2)，直线TS中的一条线段TS用以组成个单位，即用线段以度量正弦的圆的半径，在这条直线上有一点P从左向右移动，因此，他的每一点的速度都与到S点的距离成正比。他又假设了另一条直线，在这条直线上有一点Q从左向右移动，其在出发时间点时的速度P在出发点T点的速度完全相同，即Q在时出发P在T点时出发。当P在运动方向上的任意特定点时，正弦的对数或者的长度(P点到S点的剩余距离)的对数定义为表示长度的数，即当P位于时，Q从到的距离长度就为正弦的对数(或者的长度的对数)。因此，满正弦TS的对数()是0(译注：按这种定义，，Q点位于起点，行进的距离为0)，并且任意小于的正弦的对数都是正数，随着正弦逐渐减小到0而无限地递增(注：T剩余行进距离减小，但Q点距离在增大)。Napier认识到，按照这种定义，大于的数(对应直线上的，其中是P还未到达T时刻时的位置)的对数将是负值(因为满正弦时其对数已经是0)，对应的Q点的位置将在时刻的左侧。

------------------------图2 Napier定义对数假设的两条直线--------------------

令 , ... 是使得 的位置上的数，令 为P的与之对应的位置点。因此，是由相等时间内的P描述的线段。则Napier通过特殊图示的方式展示了

因此，与一系列 呈等差级数的值相对应的是一系列呈等比级数的SP值(译注：用几何表现代数)。

这件事可以用一种简明的形式来表达，它代表了Napier推理的要点(gist)，以及代表了他清晰直觉的要点。(图3 Napier对数的直观图示)

------------------------图3 Napier对数的直观图示----------------------------

令 ；并且，令p为 上任意一点，p’为 上与之对应的一点；因此， 。移动点在p点的速度相对于其在p’点的速度成常数比率 。由于这种关系对于两个间距 和 之间每一对对应点p, p’ 都成立，很显然，的移动与的移动发生在同一时间；所有点的对应速度与和 相同的比率改变。因此，这个结果遵循比率

...，

以上条件成立的条件是：假如点 …是使得 的位置上的数；即，假如线段 描述的是相同的时间。因此，呈等比级数的一组数的对数，它们本身呈等差级数。

以我们现代的记法，假如 x = SP, 我们有 ,其中V表示P在T时的速度；假如 , ；因此， ；因此，Napier的方法相当于对这个微分方程积分的直观表示。

5. 对数的极限(The limits of a logarithm)

由于没有可用的方法用以计算出任意大程度的近似值的对数，Napier 获得了两个极限，对数必须介于两个极限之间，他的整个构造方法取决于这些极限的使用，以及相应的两个数的对数之差的值的极限。

因为P和Q 在T 时刻和 时刻的速度相同(图4)，并且P的速度在此以后逐渐递减，而Q的速度保持常量不变，很显然， 。再次令在T的左侧的 表述的时间与 相同，因此， 。则，很显然，。

------------------------图4 Napier对数的直观图示----------------------------

6. Napier法则的构造(Napier's construction of the canon)

Napier在构建对数法则的过程中所采取的第一步是组成三个等比级数的数字表。第1张表由101个数字组成。其中， 是第一个数，是通比(commonratio)；因此，以现代的记法，这个表由数 组成，每一个数都是先将前一个数向右移动7位，再用前一个数减去移动过后的这个数而得到,按此方法直到生成最后一个数9999900.0004950 (图5)。

--------------------------图5 第一个表的构成方法------------------------------

第2个表51个 数组成。通比 近似等于 ，第一个表中的最后一个数(9999900.0004950)，近似等于第二个表中的第一个数(泽注：这里指的是序号的第一，即表中的第二个数9999900.000000)，同样，按此方法直到生成最后一个数9995001.222927(图6)。

--------------------------图6 第二个表的构成方法------------------------------

在这个表中，存在一个算术错误，最后一个数字应当是9995001.224804；关于这个法则的这个错误的影响将在后面涉及。最后一个数对第一个数的比率是 ，近似等于 。

第3个表由69列组成，且每列含有21个数。任意列中的第一个数可以通过前一列中的第一个数乘以 而获得。每一列第二列以后的数，都可以在前一个数的基础上乘以 而获得；第p列的第q个数是

。(如图7)

--------------------------图7 第三个表的构成方法------------------------------

后面可以观察到，最后一列的最后一个数小于半径的一半，因此，对应的角度的正弦略小于30°角的正弦。大致说来，在表中有68个数以100：99的比例插值(interpolated)在 和 之间；并且，在这些数之间，有21个数以比例10000:9995插值。(?)

Napier在制作完成这些表格之后，继续求得这些数值的足够近似的对数。为此，他关于对数极限的定理(1)和(2)是充分的。在第1个表中，9999999的对数与定理(1)是一致的，介于1.0000000和1.0000001之间,并且，Napier采用算术均值1.00000005作为所求的对数。表中的下一个正弦的对数介于2.0000000和2.0000002之间,同理，取得对数为2.00000010,再下一个正弦的对数为3.00000015，依此类推。

定理(2)用于获得与第一个表中的数几乎相等的数的对数的极限。 这样，第二个表中的第二个数9999900的对数介于100.0005050和100.0004950之间； 下一个对数的极限是这些的两倍，依此类推。因此发现第二个表中最后一个正弦的对数介于5000.0252500和 5000.0247500之间。因此，我们发现第2个表中的数的对数具有足够的近乎程度，因此，发现第二个表中一个数的对数接近1：令y为已知的正弦，x为表中最接近的正弦；假设y < x。确定z使得

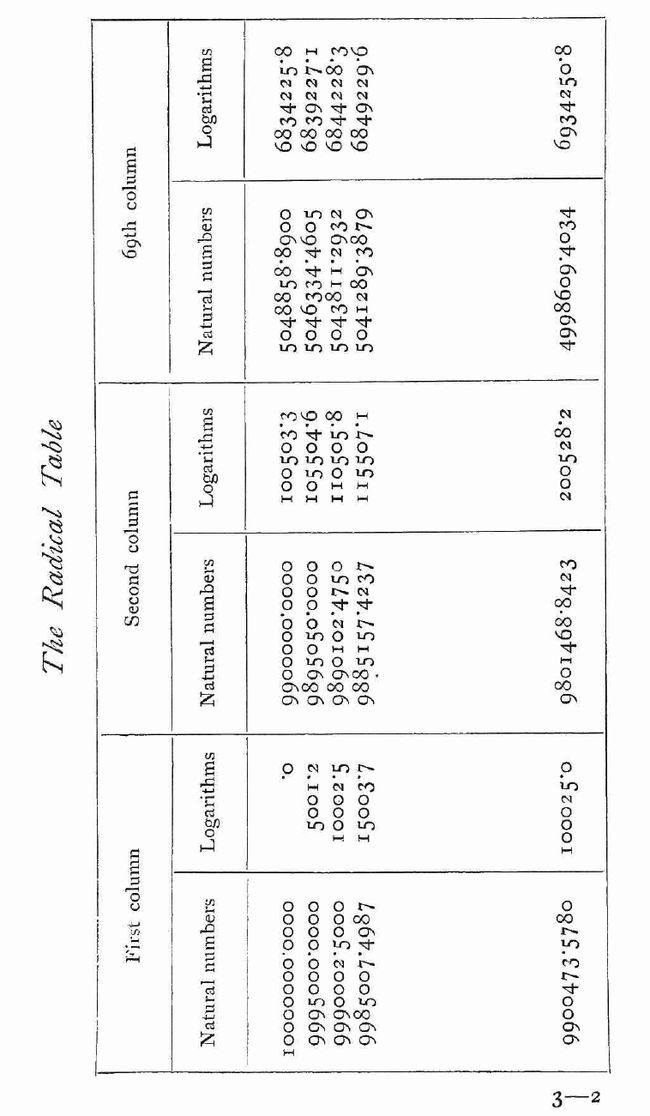
以这种方式，可求得第3个表中第一列的所有数的对数；9900473.57808的对数介于100024.9657720 和 100024.9757760之间，取这两个数的均值100024.9707740为对数。第二列中的第一个数与第一列中的最后一个数仅在第五个位码(cypher)上不同，因此可以近似计算其对数。 然后可以找到表中所有其他数字的对数，因为任何一列或任何一行中所有数字的对数都是等差级数。

当第三张表中所有数字的对数都这样计算出来时，填入这些数字形成的表被Napier称为他的基表(radicaltable)，其形式在对页中给出(图8)。

--------------------------图8 Napier制作的基表------------------------------

制作完成基表以后，将其中的对数用于主表(principal table)或法则(canon)的计算。 为此目的，非常近似等于满正弦的正弦的对数，只需从 中减去已知的正弦即可获得。 包含在基表范围内的正弦的对数可以这样求得：假设x >y；计算出 并除以x或y，或者除以x与y之间的某个数；然后将这个结果加到表的正弦的对数上。

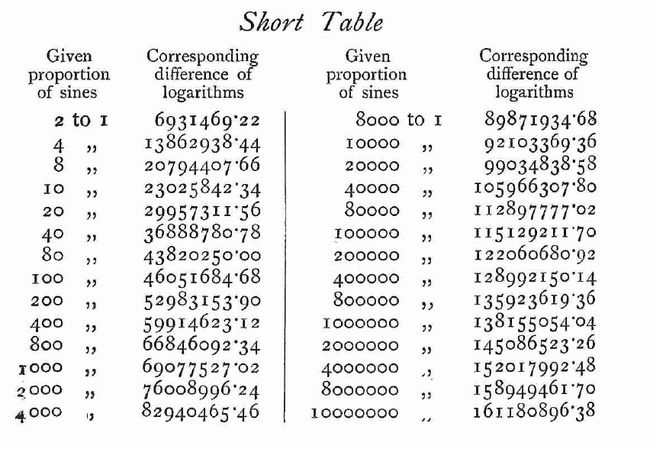
为了求得不包含在基表范围内的正弦的对数，Napier 给出了一个简表(shorttable)(图9)，其中包含两个正弦的对数之差，这两个正弦的比率是2:1和10:1的复合比率。

--------------------------图9 Napier制作的简表------------------------------

7. Napier法则的准确性(The accuracy of Napier's Canon)

上面我们已经观察到，第2个表中最后一个数的值出现了数值错误。 由于Napier在他的进一步计算中使用了这个不准确的值，因此在他的大部分对数表中产生了错误。这个错误导致的影响是，大部分的对数值比它们的正确值减少了大约 ()。 Napier本人在“构造中”中观察到，他通过他的规则求得的一些基表极限之外的数的对数，其值与通过确定根表极限的规则求得的小于45°的角的对数不同。 他将这种差异(discrepancy)归因于他使用的(employed)自然正弦值的缺陷(defects)，并建议重新计算自然正弦，应该使用作为半径。由于这两个原因，法则对数中的最后一个数字并不总是正确的。

8. Napier对数的改进系统(The improved system of logarithms)

应用到三角计算的特殊目的解释了为什么Napier的对数系统选择规定 的对数为零，并且规定 0°和 90°之间的角度的正弦的对数是正值。 然而，很明显，在一般情况下，两个数的对数之和与其乘积的对数相等的规则成立的条件是仅当单位对数取零，因为乘以单位数不会改变数的值。出于这个原因，Napier在“构造”的附录中建议对数系统的计算采用Log(1) =0，。这实际上等同于假设Log(10) =1，因为前一个假设仅表示对数要计算到小数点后10位。Briggs在他的GreshamCollege的讲座上指出，一个对数系统想要变得方便，就应当将0作为1的对数，将 作为满正弦的 (即sin(5°44'21''))的对数，相当于 。这个对数系统是他在1615年访问Merchiston期间向Napier 建议的，当时Napier指出他自己也有同样的想法，但是他假设 将导致产生最方便的系统，并且立即获得了Briggs的认可。

在上面提到的附录中，Napier 给出了一些可以用来计算改进对数的方法。这些都依赖于非常费力的五次方根和平方根的连续提取，他建议这些工作应该由其他人，尤其是Briggs来完成。在“构造”刊登的“提示”中，Napier指出，可以自由选择对数0赋值的正弦或数，经常乘以或除以满正弦(completesine或wholesine)(sin(90°)是必要的,因此如果这个正弦的对数取为零, 就可以省去麻烦。

Briggs立即着手计算这些改进的对数，并在第二年再次访问Napier时向他展示了该表的大部分内容，该表随后于1624年发表。1617年Napier去世后，开发新发明的整个工作传到了Briggs的灵巧手中，他在同年发表了他的“LogarithmorumChilias Prima(自然数从1到1000的对数)”，其中包含前一千个数字到小数点后14位的常用对数或Briggs对数。 1624年，他出版了“ArithmeticaLogarithmica(对数的算术)”，这是一张包含前 20000 个数字和从 90000 到 100000 的数字的对数表，保留14位小数。20000 和 90000 之间的差距由 Adrian Vlacq 填补，他于1628年在Gouda发表了一张从1到100000的数的常用对数表，精确到小数点后10位。Vlacq 的表虽然并非没有错误，但却构成了此后出版的所有自然数对数表的基础。

9. 关于对数的其它表(Other Tables)

1624 年，BenjaminUrsinus在科隆(Cologne)出版了与 Napier 在“Constructio(构 造)”中完全相似的对数表。角度的间隔为10''，对数给到8位。第一个以e为底的对数是John Speidell 于1619 年在伦敦发表在他的“新对数表(New Logarithmes)”中的；此表包含象限中每一分的正弦(sines)、正切(tangents)和正割(secants) 的对数，精确到小数点后 5 位。

10. Napier的前辈们(Predecessors of Napier)

通常情况下，一项伟大的新发明所涉及的基本概念都有一段历史，可以追溯到发明人之前的某个时间，通常是很长时间。尽管Napier对对数的介绍有资格被视为真正新的发明，但是，它也没有超越这个常规的规律。在此之前，古希腊数学家采用了比率的整数幂的概念；等比级数和等差级数之间对应关系的性质已被多位数学家观察到；特别是 Michael Stifel(1486-1567),著名的“Arithmetica Integra(Complete Arithmetic)(算术大全)”于 1544年出版，书中明确指出了等比级数和等差级数的运算与项之间的关系，其中这些项是对应的，即，一方面是乘法、除法和指数之间的关系，另一方面是整数的加法、减法和乘法或除法之间的关系，但Stifel或其他人没有说明如何利用这种对应关系来进行困难的算术计算。 比利时数学家Simon Stevin(1548-1620)甚至给出了一些用于计算利息的特殊表，它们由 和 的值构成。这些表中的第一个实际上是反对数表，但没有给出任何理论解释来扩展这些表的用途超出其特殊用途。对于Napier来说，无论他是否熟悉Stifel的工作，他都是第一个凭借其洞察力，将等比级数和等差级数之间的理论关系发展成为对一般算术计算最具深远重要性的方法的第一人。在理论方面，Napier的连续移动点表示涉及两个连续变量之间函数关系的概念，这本身就是数学分析发展中最重要的一步；而Stifel等人仅考虑了两个离散数字集之间的关系。

11.发明对数的一个竞争对手(A rival inventor)

如果不参考Jobst Biirgi(1552-1632年)的工作，对数发明的任何描述都是不完整的，Jobst Biirgi是一位瑞士钟表制造商和仪器制造商，他独立发明了对数系统。他的系统于 1620年发表于题为“Arithmetischeund Geometrische Progress-Tabulen(算术与几何进展一览表)”的著作中，而这时Napier的法则已广为人知并获到充分的认可。该表实际上是一个反对数表，由一组红色数字与一组黑色数字相对应组成。红色数字是0，10，20，...，这些实际是一个等差级数，而对应的黑色数字是100000000, 100010000, 100020001,...,这些实际是一个等比级数；因此，红色数字是黑色数字除以并以 为底的对数。Biirgi似乎在他发表它之前很多年就设计了他的系统，但他一直保密，直到他在Napier 的表出现六年后才发表了他的表。

12.总结(Conclusion)

Biirgi的系统明显不如Napier的系统，而在科学界传播的对数使用知识世界完全归功于Napier的工作。各国科学家一致认为，Napier应得该方法发明者的全部荣誉,它为现代世界提供了所有复杂算术计算不可或缺的工具。在“Constructio(构造)”出版之前的半个世纪里，数学科学取得了巨大进步，但英国数学家没有参与其中。非常值得注意的是，在一个被最严重的政治、社会和宗教纷争所困扰的国家，比如当时的苏格兰，竟然出现了第一个伟大的思想家，他们在17世纪将英国(GreatBritain)带到数学科学领域的最高成就点。