人工智能笔记05 约束满足——基于《人工智能》 朱福喜，清华大学出版社，2016

定义

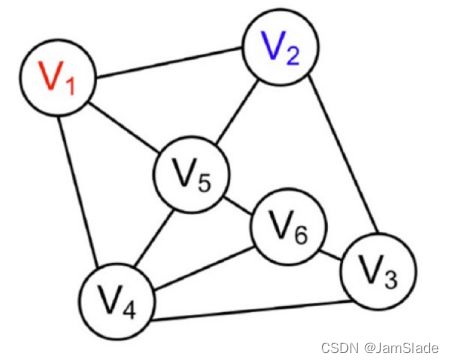
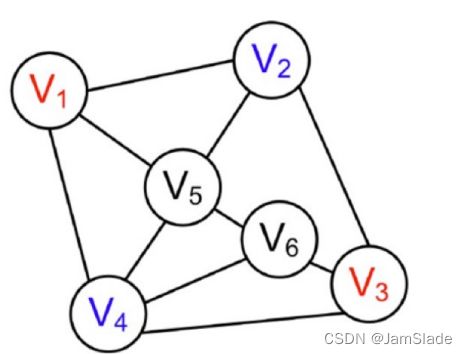
• 地图着色是指分配地图的每一个面一种颜色，使得相邻的面(指
有公共边界边)具有不同的颜色。

• 图形着色定义

Ø 考虑一个图形中的N个节点
Ø 把变量V1,…,VN的值赋给N个节点
Ø 变量取值范围{R, G, B}
Ø 约束：如果节点i和j之间有边，则Vi不同于V

• 约束满足问题 (Constraint Satisfaction Problems, CSP)

Ø CSP={V, D, C}
Ø 变量：V={V1,…,VN}，如图中节点的值
Ø 取值域：每个变量的取值范围，如D={R, G, B}
Ø 约束集：C = {C1,…,CK}
	o 每个约束有一组变量与一系列该组变量的允许取值组成，如
		[(V2, V3), {R,G},{R,B},{G,B}, {G, R},{B, R},{B, G}]
	o 通常隐式定义约束，如对每条边(i,j)，要求Vi≠Vj
	o CSP问题的解
Ø 变量：V={V1,…,VN}，具有满足所有约束要求的值
	o CSP问题特点
Ø 没有优化目标，与一般优化问题不同

二元CSP问题的约束图表示

Ø 约束与两个变量有关
Ø 节点代表变量
Ø 连线代表约束
Ø 类似着色问题

• 例子：N皇后

Ø 变量：Q1, Q2, …, QN
Ø 域：Di = {1, 2, …, N}
Ø 约束
	o Qi ≠Qj, 不在同一行
	o |Qi-Qj| ≠|i - j|，不在同一对角线

• 例子：加密问题

$$SEND+MORE=MONEY$$

Ø 变量：D,E,M,N,O,R,S,Y
Ø 域：Di = {0,1, 2, …, 9}
Ø 约束
	o M ≠0,S ≠0
	o Y=D+E或Y=D+E-10
	o D ≠E， D ≠M， D ≠ N等

求解CSP的一般搜索算法

一般图搜索策略

Ø 状态：给定K个取值，K+1,…,N个变量未取值
Ø 后继状态：给第K+1个变量赋值
Ø 初始状态：V1=?, V2=?, …, VN=?
Ø 目标状态：所有变量均赋值，并且满足所有约束要求
Ø 采用一般图搜索算法即可求解

但单纯使用DFS效率太低了

• DFS改进策略

Ø 基本思想：尽可能剪枝
Ø 只评估那些赋值，它们不违反任何与目前赋值想关的约束
Ø 不搜索那些明显不可能通往解的分支
Ø 预测合法的赋值
Ø 控制变量与值的排序

向前查看策略

Ø 对于未赋值的变量，跟踪余下的合法值
Ø 当变量无合法值时，回溯
比如这个图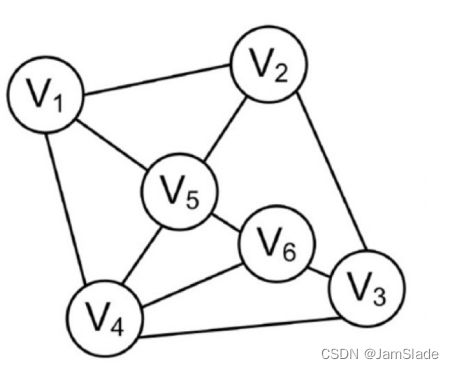

	V1	V2	V3	V4	V5	V6
R	？	？	？	？	？	？
B	？	？	？	？	？	？
G	？	？	？	？	？	？

	V1	V2	V3	V4	V5	V6
R	O	X	？	X	X	？
B		？	？	？	？	？
G		？	？	？	？	？

	V1	V2	V3	V4	V5	V6
R	O		？	X	X	?
B		O	X	？	X	?
G			?	?	?	?

	V1	V2	V3	V4	V5	V6
R	O		O	X	X	X
B		O		?	X	?
G					?	?

	V1	V2	V3	V4	V5	V6
R	O		O		X	X
B		O		O	X	X
G					?	?

	V1	V2	V3	V4	V5	V6
R	O		O			X
B		O		O		X
G					O	X

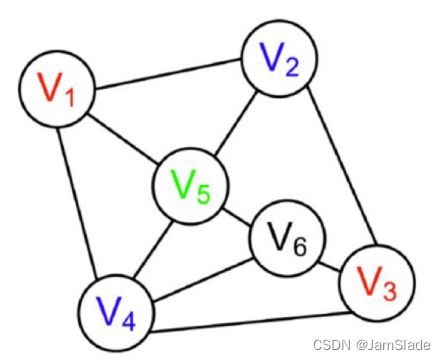
这里导致没有合法值给V6，于是回溯
在进行给V4赋值的时候，剩余值赋给V5和V6后无法保持一致性

Ø 向前查看不检查所有的不一致性，因为它只检查与当前赋值相关的约束
Ø 向前查看已经剪掉很多分支，能否看得更远？

• 约束传播策略

Ø V=在搜索的当前层次，需要赋值的变量
Ø 将D(V)中的一个值赋给V
Ø 对与V相连的每个变量V’：
	o 去掉D(V’)中与已赋值变量不一致的值
	o 对与V’相连的每个变量V”：
		- 去掉D(V”)中与已赋值变量不一致的值
		- 对与V”相连的每个变量重复执行直到不再有能被去掉的值为止
Ø 注：
	• 清理D(V’)属于已有的向前查看
	• 清理D(V”)…属于新的约束传播

第一步和前文一致

	V1	V2	V3	V4	V5	V6
R	O	X	？	X	X	？
B		？	？	？	？	？
G		？	？	？	？	？

	V1	V2	V3	V4	V5	V6
R	O		X	X	X	?
B		O	X	？	X	X
G			?	X	?	X

因为V2蓝色之后
V5只能给绿色，然后V5给绿色之后依次迭代下去直到出现“分支”或者“不满足条件”或者直接得到“解”


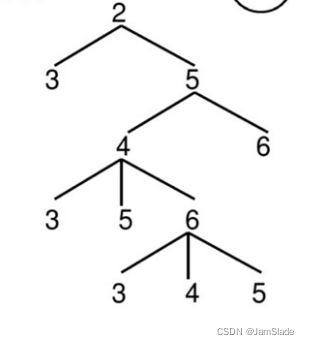
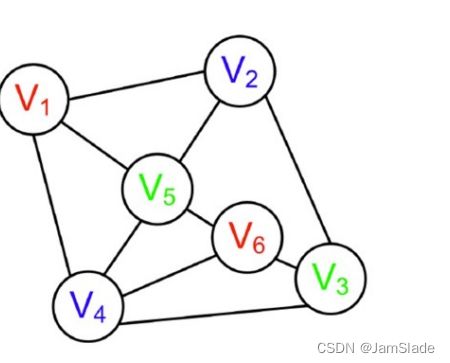
如果没找到解就说明这个DFS有问题，可以快速回溯

求解CSP的启发式算法

• 变量与值的启发式算法
Ø 一般搜索算法中，是以一个固定的次序来选择下一个变量和下一个值
Ø 问题：
• 有更好的方法来选择下一个变量吗？
• 有更好的方法来选择下一个赋值给当前变量吗？

• 变量排序

Ø 最多约束变量(MCV)
Ø 选择一个贡献最多约束数的变量，会对其它变量有极大的影响，因此有
希望裁剪掉大部分搜索
Ø 要求：在约束图中找到与最多变量相连的变量
类似拓扑排序

Ø 最少余下值(MRV)
Ø 选择一个侯选值最少的变量，由此极可能导致一个早期的失败(失败优先
启发式策略)

• 值排序

Ø 最少值约束(LCV)
Ø 选择使相邻变量可用值减少最少的值
Ø 优先选用最有可能的值（也即为随后的变量赋值提供最大的灵活性）来
获得一个解

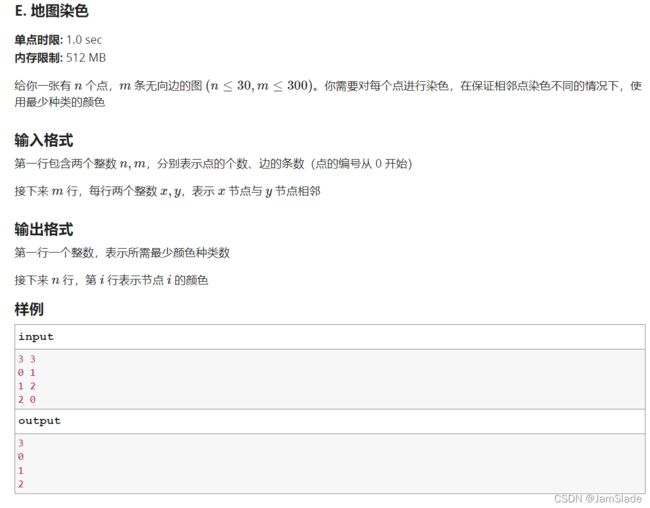
题目测试： 地图染色

思路

这个数量级直接DFS就行，甚至不需要过多的剪枝

代码

#include
#include
#include
#include

using namespace std;
const int maxn = 1005;
int n,m;
int all = 0x3f3f3f3f;//最小颜色量
int map[maxn][maxn];//图
int color_to_point[maxn][maxn];//一个颜色
int color_num[maxn];
int color[maxn];//最后输出的out
int color_final[maxn];

void out()//最终输出
{
    cout << all << endl;
    for(int i = 0; i < n; i++)
        cout << color_final[i] << endl;
}

void change()//改最小情况
{
    for(int i = 0; i < n; i++)
        color_final[i] = color[i];
}

void dfs(int seq, int total) // seq 表示第几个人， tot表示已经用了的颜色
{
    if(total >= all)
        return;
    if(seq == n)//鉴定完前n个
    {
        if(all > total)//最优情况迭代
        {
            all = total;
            change();
        }
        return;
    }
    for(int i = 0; i < total; i++)
    {
        //遍历所有使用过的颜色
        int size = color_num[i];
        int not_counter = 0;
        for(int j = 0; j < size; j++)
        {
            int to_judge = color_to_point[i][j];
            if(!map[to_judge][seq])//seq对应的点和这个是否相邻？
            {
                not_counter++;
            }
        }
        if(not_counter == size)//所有点都不冲突
        {
            color[seq] = i;//保存节点颜色
            color_to_point[i][color_num[i]++] = seq;//并储存好
            dfs(seq + 1, total);
            //回溯
            color_num[i]--;
            //color[seq] = -1;
        }
    }
    color[seq] = total;//已经选了的颜色都有冲突
    color_to_point[total][color_num[total]++] = seq;//选一个新的颜色
    dfs(seq + 1, total + 1);
    //回溯
    color_num[total]--;
    //color[seq] = -1;

}

int main()
{
    memset(map, 0 ,sizeof(map));
    memset(color_to_point,0, sizeof(color_to_point));
    memset(color_num,0,sizeof(color_num));
    memset(color, -1, sizeof(color));
    memset(color_final, 0 ,sizeof(color_final));
    cin >> n >> m;// amounts of points and edges
    
    int x, y;
    for(int i = 0; i < m; i++)
    {
        color[i]=-1;
        cin >> x >> y;
        map[x][y] = map[y][x] = 1;
    }
    dfs(0,0);
    out();//
}

题目测试：字符路径

思路1

DFS暴力穷举，然后发现平均每次开五个节点
复杂度可以到达$5^{26}$次妥妥超时

所以找寻DP思路

思路2

利用DP思想，我们可以将每次走“1步“视为一个状态

例如road路径给的是”abcd"
那么每次我们要求的是a->d，那么我们先得求出a->c和a->b的状态
而这里的状态用一个二维数组保存

我们先假定a点有n个，b点m个，c点x个
具体的保存形式就是：
a->b 用$n\times m$大小得数组进行储存，每个a到b之间的最短距离

那么再状态转移的时候，利用floyed或者dijkstra的图算法，来利用b->c和一开始村好的a->b来计算出来$n\times x$个a到c的最短路径

最后求到a->d的所有可能，再遍历一遍得到最终的最短路径

代码

思路一代码

#include
#include
#include
#include

using namespace std;

struct point
{
    int x;
    int y;
    int last_point_dis;
};


typedef vector<point> vp;
typedef map<char,vp> mcv;


const int maxn = 1024;
int ans = 0x3f3f3f3f;
int len;
char MAP[maxn][maxn];

int cal_Man(point a, point b)
{
    return abs(a.x - b.x) + abs(a.y-b.y);
}
void test_map(const mcv& ma)
{
    for(mcv::const_iterator it = ma.begin(); it != ma.end(); it++)
    {
        cout << it->first << ":\n";
        for(vp::const_iterator itt = it->second.begin(); itt != it->second.end(); itt++)
        {
            cout << itt->x << "  y: " << itt->y << " dis:" << itt->last_point_dis<< endl;
        }
    }
}
int cmp(point a, point b)
{
    return a.last_point_dis < b.last_point_dis;
}

void dfs(mcv ma, string& str, point prev, int depth, int cost = 0)
//由于避免dfs后续影响前部分内容这里不用引用ma
{
    if(cost > ans) return;
    if(depth > len)
        return;
    if(depth == len)
    {
        if(cost < ans)
        {
            ans = cost;
        }
        return;
    }

    char seq = str[depth];
    for(vp::iterator it = ma[seq].begin(); it != ma[seq].end(); it++)
    {
        it->last_point_dis = cal_Man(*it, prev);
    }
    sort(ma[seq].begin(), ma[seq].end(), cmp);//end就不用加size了
    //test_map(ma);
    for(vp::iterator it = ma[seq].begin(); it != ma[seq].end() && it != ma[seq].begin() + 3; it++)
    {
        dfs(ma, str, *it, depth + 1, cost + it->last_point_dis);
    }
}

int main()
{
    mcv ma;
    int n, m ,k;
    cin >> n >> m >> k;
    for(int i = 0; i < n; i++)
        for(int j = 0; j < m; j++)
        {
            cin >> MAP[i][j];
            ma[MAP[i][j]].push_back({j, i, 0});
        }
    //test_map(ma);
    string road;
    cin >> road;
    len = road.length();
    char zero = road[0];
    for(vp::iterator it = ma[zero].begin(); it !=ma[zero].end(); it++)
    {
        dfs(ma, road, *it, 1);
    }
    cout << ans;
}

思路二

#include
#include
#include
#include

using namespace std;

struct point
{
    int y;
    int x;
};


typedef vector<point> vp;
typedef unordered_map<char,vp> mcv;


const int inf = 0x3f3f3f3f;
const int maxn = 105;

int ans = inf;
int len;
char MAP[maxn][maxn];
int start_mid[maxn][maxn];
int mid_next[maxn][maxn];
string road;

int cal_Man(point a, point b)
{
    return abs(a.x - b.x) + abs(a.y-b.y);
}

void test_map(const mcv& ma)
{
    for(mcv::const_iterator it = ma.begin(); it != ma.end(); it++)
    {
        cout << it->first << ":\n";
        for(vp::const_iterator itt = it->second.begin(); itt != it->second.end(); itt++)
        {
            cout << itt->x << "  y: " << itt->y << endl;
        }
    }
}

void array_init(mcv& ma)
{
    char zero = road[0];
    int zero_num = ma[zero].size();
    char one = road[1];
    int one_num = ma[one].size();
    
    for(int i = 0; i < zero_num; i++)
    {
        for(int j = 0; j < one_num; j++)
        {
            start_mid[i][j] = cal_Man(ma[zero][i], ma[one][j]);
            //cout << start_mid[i][j] << " ";
        }//cout << endl;
    }
}

void dp(mcv& ma, int depth)
{
    //test_map(ma);
    char mid = road[depth - 1];
    int mid_num = ma[mid].size();
    char next = road[depth];
    int next_num = ma[next].size();

    for(int i = 0; i < mid_num; i++)
    {
        for(int j = 0; j < next_num; j++)
        {
            mid_next[i][j] = cal_Man(ma[mid][i], ma[next][j]);
        }
    }
    
    char zero = road[0];
    int zero_num = ma[zero].size();
    int temp[maxn][maxn];
    memset(temp, inf, sizeof(temp));

    // cout << zero_num <<" " << mid_num << " "<
    // cout << next << endl;
    // cout << zero << mid << next << endl;
    for(int k = 0; k < mid_num; k++)
        for(int i = 0; i < zero_num; i++)
            for(int j = 0; j < next_num; j++)
                if(temp[i][j] > start_mid[i][k] +  mid_next[k][j])
                    temp[i][j] = start_mid[i][k] +  mid_next[k][j];

    for(int i = 0; i < zero_num; i++)
        for(int j = 0; j < next_num; j++)
            start_mid[i][j] = temp[i][j];
    
    // for(int i = 0; i < zero_num; i++){
    //     for(int j = 0; j < next_num; j++)
    //         {cout << temp[i][j] << "..";}
    //         cout << endl;}
    //cout << "?" << endl;
}
int main()
{
    
    int n, m ,k;
    cin >> n >> m >> k;
    mcv ma;


    for(int i = 0; i < n; i++)
        for(int j = 0; j < m; j++)
        {
            cin >> MAP[i][j];
            ma[MAP[i][j]].push_back({i,j});
        }
    // for(int i = 0; i < n; i++)
    //     for(int j = 0; j < m; j++)
    //         cout << MAP[i][j] << " ";
    


    cin >> road;
    len = road.length();
    array_init(ma);//初始化start_mid;
    
    for(int i = 2; i < len; i++)
    {
        dp(ma, i);
    }
    
    int zero_num = ma[road[0]].size();
    int next_num = ma[road[len-1]].size();
    for(int i = 0; i < zero_num; i++)
        for(int j = 0; j < next_num; j++)
            //cout << start_mid[i][j] << " ";
            if(ans > start_mid[i][j])
                ans = start_mid[i][j];
    
        cout << ans;
}