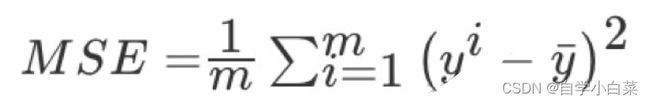机器学习案例2:基于线性回归的波士顿房价预测
案例2:基于线性回归的波士顿房价预测
为什么写本博客
前人种树,后人乘凉。希望自己的学习笔记可以帮助到需要的人。
需要的基础
懂不懂原理不重要,本系列的目标是使用python实现机器学习。
必须会的东西:python基础、numpy、pandas、matplotlib和库的使用技巧。
说明
完整的代码在最后,另外之前案例中出现过的方法不会再讲解。
目录结构
文章目录
-
- 案例2:基于线性回归的波士顿房价预测
-
- 1. 涉及到的新方法说明:
- 2. 数据集介绍与划分:
- 3. 数据标准化:
- 4. 模型创建、训练和评估:
- 5. 总结与完整代码:
1. 涉及到的新方法说明:
数据集加载
from sklearn.datasets import load_boston
# 加载数据
data = load_boston()
标准化
from sklearn import preprocessing
# 数据标准化: 即化为均值为0,方差为1的分布
standard = preprocessing.StandardScaler()
# 将训练集和测试集x数据进行表转化
x_train = standard.fit(x_train)
x_test = standard.fit(x_test)
模型创建
from sklearn.linear_model import LinearRegression
model = LinearRegression()
均方误差MSE
sklearn.metrics.mean_squared_error(y_true, y_pred)
# 参数: 真实值和预测值
2. 数据集介绍与划分:
波士顿房价数据,共506条,每条13个特征,加上一个标签(即房价值)。当然,我们可以对特征进行分析,然后选取相关性较强的属性来进行线性回归拟合,但是,这里我们就不管这么多,直接把所有数据都放入,相当于一个多元线性回归。
然后,我们将数据7:3划分为训练集和测试集:
from sklearn.datasets import load_boston
from sklearn import model_selection
# 加载数据
data = load_boston()
# print(data)
# 划分数据集
x_train,x_test,y_train,y_test = model_selection.train_test_split(data['data'],data['target'],test_size=0.3,random_state=20)
print(x_train.shape) # (354, 13)
print(y_train.shape) # (354,)
3. 数据标准化:
下面,我们需要将数据进行标准化,这一步很简单,根据方法来即可:
from sklearn import preprocessing
# 数据标准化: 即化为均值为0,方差为1的分布
standard = preprocessing.StandardScaler()
# 将训练集和测试集x数据进行表转化
x_train = standard.fit_transform(x_train)
x_test = standard.fit_transform(x_test)
4. 模型创建、训练和评估:
首先,创建和训练模型:
# 创建模型
model = LinearRegression()
# 训练
model.fit(x_train,y_train)
接着,对模型进行评估,这里我们使用MSE进行评价,MSE就是真实值和预测值差的平方和的平均,用公式表示为:
当然,不难看出MSE值越小模型越好,因为这样预测值和真实值的插值才小。
因此,我们使用MSE评估,并打印相关参数:
# MSE
y_pred = model.predict(x_test)
score = sklearn.metrics.mean_squared_error(y_test,y_pred)
print('MSE = ',score) # MSE = 25.70195952797909
# 打印相关参数
print('w = ',model.coef_)
print('b = ',model.intercept_)
相关打印结果如下:
MSE = 25.70195952797909
w = [-0.47142056 0.6541109 0.25721446 0.55846116 -2.34588302 3.34540835
0.27632621 -2.67132414 1.94525301 -1.70458238 -1.84255136 0.84011202
-3.35643536]
b = 22.684745762711895
5. 总结与完整代码:
线性回归是一个非常简单的模型,但是这个模型却有非常好的数学可解释性,因此也是一个非常常用的模型之一。
完整代码:
# author: baiCai
# 导入包
import sklearn
from sklearn import preprocessing
from sklearn import model_selection
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
# 加载数据
data = load_boston()
print(data)
# 划分数据集
x_train,x_test,y_train,y_test = model_selection.train_test_split(data['data'],data['target'],test_size=0.3,random_state=20)
print(x_train.shape) # (354, 13)
print(y_train.shape) # (354,)
# 数据标准化: 即化为均值为0,方差为1的分布
standard = preprocessing.StandardScaler()
# 将训练集和测试集x数据进行表转化
x_train = standard.fit_transform(x_train)
x_test = standard.fit_transform(x_test)
# 创建模型
model = LinearRegression()
# 训练
model.fit(x_train,y_train)
# MSE
y_pred = model.predict(x_test)
score = sklearn.metrics.mean_squared_error(y_test,y_pred)
print('MSE = ',score) # MSE = 25.70195952797909
# 打印相关参数
print('w = ',model.coef_)
print('b = ',model.intercept_)