离散数学：二元关系

笛卡儿积

给定两个集合 A 和 B，笛卡儿积记为 A × B = {|x∈A, y∈B}。

举例说明

A = {a, b}，B = {c, d}，求 A × B。
解： A × B = {a, b} × {c, d} = {,,,}

---

二元关系

给定两个集合 A 和 B，R 是笛卡儿积 A × B 的任意子集，则称 R 为从 A 到 B 的一个二元关系。

举例说明

若 A × B = {,,,}
则 为从 A 到 B 的一个二元关系。

---

二元关系的表示

关系矩阵表示法

给定两个集合 A 和 B，R 是 A 到 B 的二元关系，用集合 A 的元素标注矩阵的行，用集合 B 的元素标注矩阵的列。当 a∈A，b∈B，若 ∈ R 则在矩阵的 a 行 b 列标注 1，若 ∉ R 则在矩阵的 a 行 b 列标注0。所得矩阵为 R 的关系矩阵。

举例说明

A = {a, b}，B = {c, d}，R = {, }, 求 R 的关系矩阵。
解：

A\B	c	d
a	0	1
b	0	1

R 的关系矩阵

0	1
0	1

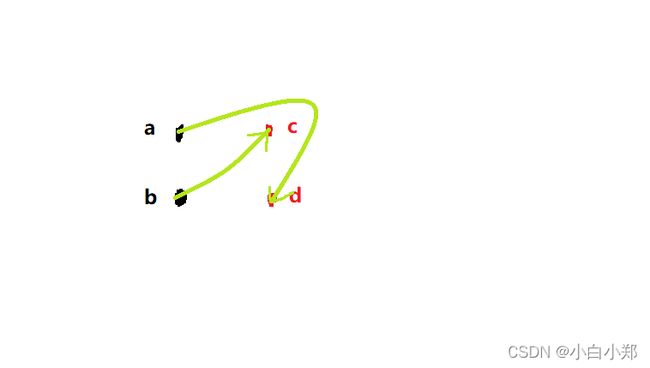
关系图表示法

给定两个集合 A 和 B，R 是 A 到 B 的二元关系，集合 A 内元素个数为 n_A ，集合 B 内元素个数为 n_B 。在平面上作出 n_A 个结点标记为a₁, a₂,…,a_n，在平面上作出 n_B 个结点标记为b₁, b₂,…,b_n。若 R 内存在 x, b_y> 则从结点 a_x 到结点 b_y 作出一条有向弧。

举例说明

A = {a, b}，B = {c, d}，R = {, }, 求 R 的关系图。
解：