离散数学-二元关系

序偶与有序n元组

由两个对象x、y组成的序列称为有序n元组，也称之为序偶，记作,称x,y为其中的第一元素和第二元素。
序偶中的x,y有次序。
如果和两个序偶，如果x=u且y=v,则两个序偶相等。
有序三元组是一个序偶，其第一个元素也是一个序偶。<,c>是有序三元素，简记作，>则不是
有序n元组是一个序偶，其第一个元素本身是一个有序n-1元组，记作<,xn>

集合的笛卡尔积

设集合A、B，由A的元素为第一元素，B的元素为第二元素组成的全部序偶的集合，称为A和B的笛卡尔积，记作AXB

集合笛卡尔积不满足交换律，结合律

集合笛卡尔积运算的性质
（1）如果AB都是有限集，且|A|=m,|B|=n,则|AXB|=mn
（2）AX∅=∅XA=∅
（3）X对∪和∩满足分配律


（4）若C≠∅，则A⊆B⇔AXC⊆BXC⇔CXA⊆CXB

（5）设ABCD为非空集合，则AXB⊆CXD⇔A⊆C∧B⊆D

（6）由于X不满足结合律，所以约定

关系的基本概念

定义1 :设A、B是集合，如果R⊆AXB,则称R是一个从A到B的二元关系。如果R⊆AXA，则称R是A上的二元关系。二元关系简称为关系。
定义2:任何序偶的集合，都称之为一个二元关系。例如:R={<1,a>, <书,车>, <人,树>}

关系时序偶（点）的集合（构成线、面）如坐标轴上的关系
关系的定义域：设R⊆AXB，由所有∈R的第一个元素组成的集合，称为R的定义域。记作dom R,

关系的值域：设R⊆AXB，由所有∈R的第二个元素组成的集合，称为R的值域，记作ran R,即

关系的表示方法

枚举法：即将关系中所有序偶一一列举出，写在大括号内。
谓词公式法：即用谓词公式表示序偶的第一个元素与第二元素间的关系。例如
R={|x 有向图法：
R⊆AXB，用两组小圆圈（称为结点）分别表示A和B的元素，当∈R时，从x到y引出一条有向边，这样得到的图形称之为R的关系图。

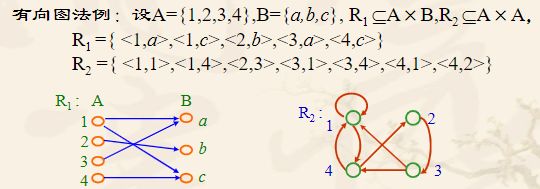
矩阵法：

特殊关系

空关系∅
空关系是没有任何元素的关系，它的关系图中只有结点，没有任何边；矩阵中全是0

完全关系（全域关系）
设有限集合A,B，AXB（或AXA）本身也是一个从A到B（或A上）的关系，称之为完全关系。例如定义在{1,2,3}上的完全关系。
显然，完全关系是包括集合笛卡尔积中全部序偶的关系，矩阵中全是1.

恒等关系
IA⊆AXA,且IA={|x∈A},称为A上的恒等关系。

关系的集合运算。
由于关系是集合，所以集合的∩，∪，-，对称差和~运算对关系也适用。

关系的性质

自反性

定义:设R是集合A中的关系，如果对于任意x∈A都有∈R (xRx)，则称R是A中的自反关系，即

例如：实数集合上的<=关系就是自反关系，因为对任意实数x，有x<=x
自反关系有向图的特点:每个结点都有环。
自反关系矩阵的特点:主对角线都为1。

反自反性

定义:设R是集合A中的关系，如果对于任意的x∈A， 都有∉R,则称R为A中的反自反关系，即

实数集合上的<关系是反自反关系；
人群中的父子关系是反自反关系
反自反关系的有向图特点：每个结点都无环
反自反关系矩阵的特点：主对角都为0

对称性

R是集合A中关系，若对任何x, y∈A,如果有xRy,必有yRx,则称R为A中的对称关系,即

例如：人群中的邻居关系和朋友关系都是对称关系。
对称关系有向图的特点：在两个不同的结点之间，若有边的话，则有方向相反的两条边
对称关系矩阵的特点：以主对角线对对称的矩阵。

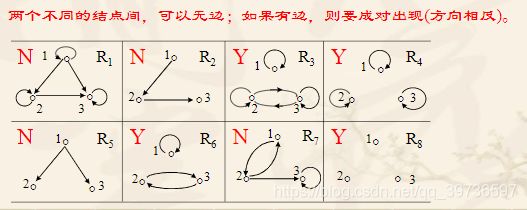
反对称性

设R为集合A中关系，若对任何x, y∈A,如果有xRy和yRx,则有x=y,则称R为A中反对称关系,即

例如：实数集合上的<=关系就是反对称的关系。
反对称关系有向图的特点:两个不同的结点之间最多有条边。反对称关系矩阵的特点:以主对角线为对称的两个元素中最多有一个 1

传递性

R是A中关系，对任何x,y,z∈A,如果有xRy和yRz,就有xRz,则称R为A中传递关系，即

例如：实数集中的<=,<,集合包含于，真包含于是传递的。
从关系有向图和关系矩阵中不易看清是否有传递性，必须直接根据传递的定义来检查。
传递性定义的谓词公式形式的前件为F时，整个表达式为T,传递性成立，即若xRy与yRz中至少有一个是F时，前件为假，R是传递的。

判断传递性的典型图例
独立无环的结点不影响传递性
空关系是传递的
独立有环的结点不影响传递性
恒等关系是传递的
完全关系是传递的

关系的复合运算

1、基本概念

现实中，由两个关系可生成一种新的关系，例如，现有a,b,c三人，A={a,b,c},R是A上的兄妹关系，S是A上的母子关系。
已知，∈R∧∈S,即
a是b的哥哥，b是a的妹妹
b是c的母亲，c是b的儿子。
a和c之间就是舅舅和外甥的关系，记作R·S，称作R和S的复合。

定义：
设R是从X到Y的关系，S是 从Y到Z的关系，则R和S的复合关系是从X到Z的关系，记作R·S

2、计算方法

2.1.有向图法

2.2.枚举法

2.3.谓词公式法

设I是实数集合，R和S都是I上的，其中

谓词公式法计算关系的复合实际上就是函数的代入过程。

3、计算方法

关系复合运算不满足交换律
1.关系复合运算满足结合律


2.已知R⊆AXB,S⊆BXC,T⊆BXC,则
3.如果R是从A到B的关系，则R·IB=IA·R=R;

4.关系的乘幂
令R是A上关系，由于复合运算可结合，所以关系的复合可以写成乘幂形式。即
R·R=R2,R·R·R=(R·R)·R=R2·R=R3
R·R…·R=Rn
特别的，定义R0=IA
设m,n为非负整数。显然，有
(1)Rm·Rn=Rm+n
(2)(Rm)n=Rm·Rm…=Rmn

关系的求逆运算

定义：R是从A到B的关系，如果将R中的所有序偶的两个元素的位置互换，得到一一个从B到A的关系，称之为R的逆关系，记作Rc, 或R-1。

根据定义，RC是将R中 所有的序偶的两个元素的位置互换。
RC的有向图:是将R的有向图的所有边的方向颠倒。
RC的矩阵MRc = (MR)T ,即为R矩阵的转置。例如

令R、S都是从X到Y的关系，则


8.设R是A上的关系，则R是对称的，当且仅当Rc=R

关系的闭包运算

基本概念

关系的闭包是通过关系的复合和求逆运算构成的一个新的关系，新关系满足某些特性。
具体来说，给定A中关系R,如图所示，显然R不是自反的，不是对称的，也不是传递的，我们要求相应的闭包

定义:给定A中关系R，若A上 另一个关系R’,满足 :
(1)R⊆R’;
(2)R’是自反的
(3)R’是“最小的”（包含的序偶最少），即对于任何A上的自反关系R’’，如果R⊆R’’，就有R’⊆R’'
则称R’是R的自反闭包，记作r®
如果R’是包含R的最小的对称关系，则称R’是R的对称闭包，记作s®
如果R’是包含R的最小的传递关系，则称R’是R的对称闭包，记作t®

定理1：给定A中关系R,则r®=R∪IA

定理2：给定A中关系R，则s®=R∪R-1
定理3：给定A中关系R，则t®=R∪R2∪R3∪…


疑问:用上述公式计算t( R )，要计算R的无穷大次幂,似乎无法实现。真实情况是这样的吗?请看下面的例子:

定理4.给定A中关系R,如果A是有限集合，|A|=n,则
t( R )=R∪R2…Rn
此外，求关系R的传递闭包t®,还可以基于R的关系矩阵。

运算性质

定理5：R是A上关系，则
(1)R是自反的，当且仅当r( R )=R
(2)R是对称的，当且仅当s( R )=R
(3)R是传递的，当且仅当t( R )=R

定理6. R是A上关系，
则
(1) R是自反的，则s( R )和t( R )也自反。
一个自反关系的三个闭包都自反（r( R )显然自反）
(2)R是对称的，则r( R )和t( R )也对称。
一个对称关系的三个闭包都对称(s®显然对称)
(3)R是传递的，则r( R )也传递
一个传递关系的自反闭包传递，对称闭包不一定传递。

集合的划分与覆盖

1.覆盖：设X是一个非空集合，A={A1,A2,…,An},A≠∅，Ai⊆X(i=1,2,…n),如果满足A1∪A2∪…∪An=X,则称A为集合X的一个覆盖
2.划分：设A={A1,A2,…,An}是X的一个覆盖，且Ai∩Aj=∅(i≠j,1<=i,j<=n),则称A是X的划分，每个Ai均称为这个划分的一个划分类。
注意：划分一定是覆盖，但覆盖不一定是划分。
最小划分:划分块最少的划分。即只有一个划分块的划分，这个划分块就是X本身。 如A1={{1,2,3}}。
最大划分:划分块最多的划分。即每个划分块里只有一个元素的划分。
如A2={{1},{2},{3}}。

A1,A2,A3是一种划分，其中A1是最小划分，A2是最大划分。

例: X是全体东北大学学生的集合，A和B都是X的划分:
A={东大男生，东大女生}
B={辽宁籍东大同学非辽宁籍东大同学}
令C={辽宁籍东大男生,辽宁籍东大女生，非辽宁籍东大男生,非辽宁籍东大女生}
显然，C是X的划分，是A与B两种划分的交叉划分。

等价关系与等价类

1.等价关系

定义：设R是A上的关系，若R是自反的、对称的和传递的，则称R是A上的等价关系。
若a,b∈A，R是等价关系，且aRb,则称a与b等价。

2.等价关系的有向图
（1）完全关系（全域关系AXA）图
下面分别是当A中只有1、2、3个元素时的完全关系图

模3同余关系R的关系图


从关系图可以看出R是自反、对称、传递的关系，所以R是等价关系。
等价关系R的有向图由若干个独立子图构成的，每个独立子图都是完全关系图

思考题: A={1,2,3},可构造多少个A中不同的等价关系?
解:可以根据等价关系有向图的特点来考虑。如果等价关系R中有:
a)三个独立子图的情形，则(1 )个等价关系。
b)二个独立子图的情形，则(3)个 等价关系。
c)一 个独立子图的情形，则(1)个等价关系。
一共有(5)个中不同的等价关系。

2.等价类

由等价关系图求等价类
R的关系图中每个独立子图上的结点，构成一个等价类
独立子图个数=不同的等价类的个数

等价类的性质

含义：同一个等价类中的元素，彼此有等价关系R







(4)A中任何元素a,a必属于且仅属于一个等价类


(6)R的所有等价类构成的集合是A的一个划分

3.商集

R是A上等价关系，由R的所有等价类构成的集合称之为A，关于R的商集。记作A/R。即
A/R={[a]R |a∈A}


定理：集合A上的等价关系R,决定了A的一个划分，该划分就是商集A/R


若A={A1,A2,…An}是X的一个划分，则可以构造一个X上的等价关系R，使得X/R=A

集合X的一个划分可以确定X上的一个等价关系

偏序关系

定义：R是A上自反、反对称和传递的关系，则称R是A上的偏序关系，并称是偏序集。
例如：数值的<=,>=关系和集合的包含关系都是偏序关系
用符号<=表示任意偏序关系，但要注意，这里的<=不一定是小于或等于的含义。


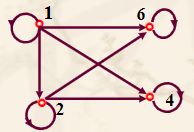
偏序关系有向图的特点：
每个结点都有环（自反性）
不同结点之间可以没有边，如果有边，则至多一条边（反对称性）
由于有(a,b)∈R和(b,c)∈R,则(a,c)∈R（传递性）
简化关系图：

哈斯图

偏序集中的重要元素

极大元与极小元

注意1：A中的极大元与极小元要在A（子集）中寻找，不要到P(全集)中寻找。

注意2：极大元、极小元不要求唯一，且同一元素，可以既是极大元，又是极小元，如5,7

最大元与最小元

注意：A中的 最大元与最小元要在A（子集）中寻找，不要到P(全集)中寻找。

是偏序集，B是A的非空子集，如果B有最小元（最大元），则最小元（最大元）是唯一的。

小结：是偏序集，B是A的非空子集
（1）B的极小元总是存在的，就是子集哈斯图中处在最下层的元素，B的极大元也总是存在的，就是子集哈斯图中处于最上层的元素。
（2）B的最小元（最大元）有时可能不存在，只要有唯一的极小（大）元，则这个极小（大）元就是最小（大）元。否则，就没有最小（大）元。

3.上界与下界

注意：A的上下界要到P(全集)中寻找，不局限于A(子集）

上确界和下确界

说明：
上确界：所有上界中的最小者，最小上界
下确界：所有上界中的最大者，最大上界
另外，如果存在上下确界，则上下确界一定是唯一的。