图像处理的常用空间滤波算法
三种常见的模糊图像滤波算法：均值滤波、高斯滤波、中值滤波。
均值滤波
用滤波掩膜确定的领域内像素的平均灰度值去代替图像的每个像素点，目的是为了“减噪”。
缺点：存在不希望的边缘模糊效应。
高斯滤波
高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，高斯滤波器是一类根据高斯函数的形状来选择权值的线性平滑滤波器。在对图像进行卷积的时候其实是对图像进行点操作，用所求像素点周围的像素通过模板的权值计算得到新的像素值。而图像形状的不同也就代表了不同的参数，从而得到不同的模板。
二维高斯分布：
A：表示高斯分布的峰值，（
,
）表示均值，
表示方差，其中假设了
，即在x轴与y轴方向的方差相同。
当且仅当
时，二维高斯函数为正太分布随机变量的概率密度函数，高斯函数的曲面下的积分为1：
为什么需要二维高斯函数的积分为1呢？
我的理解是，我们是希望我们基于高斯函数设计的高斯核不会使得卷积之后的像素值超过255，假如说一个3*3的卷积核用来处理像素值均为255的一个原图像的区域，那么得到的中心点的像素值为255*(卷积核的和)，只有当卷积核的和为1时，此时中心点的像素值不会超过255。
我们设计高斯核是基于高斯函数设计的，也就是说我们的高斯核的形状与高斯函数保持一致。因此高斯核有如下特点：
- （x,y）均值为卷积核的中心点坐标（kSize-1）/2，kSize为卷积核的大小。比如3*3的卷积核，其中心点坐标为（1,1），图像坐标从0开始。
- 卷积核的方差
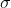根据卷积核的大小kSize计算，在Opencv中的GaussianBlur函数原型是这么设计方差的：σ=0.3((ksize−1)×0.5−1)+0.8。我们可以通过方差来计算卷积核大小，也可以通过卷积核大小来计算方差。 - 需要归一化处理，使得高斯核的和为1。
参考博文：高斯滤波及其原理_声希Censh的博客-CSDN博客_高斯滤波
参考博文中给出了自己创建高斯卷积核的C的源代码：
代码中用的高斯函数是：
，所以在归一化之前，卷积核中心点的值为1。卷积核采用的归一化方法为：高斯核各点的值/sum，sum为高斯核的和。
#include
#include
double** createGuassion(int, double);
double** createGuassion(int kSize, double sigma)
{
if (kSize % 2 == 0 || kSize < 0 || (kSize == 0 && sigma == 0))
{
return 0;//当模板大小为偶数、或者小于0、或者模板大小与sigma同时为0时返回
}
else if (kSize == 0)
{
kSize = 2 * (sigma - 0.8) / 0.3 + 3;
kSize = round(kSize);//
if (kSize % 2 == 0)
{
kSize += 1;
}
}
else if (sigma == 0)
{
sigma = 0.3 * ((kSize - 1) * 0.5 - 1) + 0.8;//sigma缺省时，利用该公式计算sigma
}
double** guass;//生成的高斯矩阵
double sum = 0;//用于归一化求和
double x2 = 0;
double y2 = 0;
int center = (kSize - 1) / 2;//高斯核中心点的行标和列标（从0开始计），所以必须保证kSize为奇数
guass = new double* [kSize];//注意，double*[k]表示一个有10个元素的指针数组
for (int i = 0; i < kSize; ++i)
{
//先创建一个kSize×kSize的模板矩阵
guass[i] = new double[kSize];
}
for (int i = 0; i < kSize; i++)
{
x2 = pow(double(i - center), 2); //高斯函数中的x平方
for (int j = 0; j < kSize; j++)
{
y2 = pow(double(j - center), 2);//高斯函数中的y平方
sum += guass[i][j] = exp(-(x2 + y2) / (2 * sigma * sigma));//赋值并累加
}
}
//归一化处理
if (sum != 0)
{
for (int i = 0; i < kSize; i++)
{
for (int j = 0; j < kSize; j++)
{
guass[i][j] /= sum;
}
}
}
return guass;
}
int main()
{
double** p = createGuassion(3, 0);
for (int i = 0; i < 3; ++i)
{
for (int j = 0; j < 3; ++j)
{
printf("%-9f\x20", *(*(p + i) + j));
//p+i表示a[i]的地址
//"%-9f中, '-'表示左对齐(无'-'默认为右对齐)；9表示这个元素输出时占两个空格的空间
//"\x20"表示以十六进制数20所代表的字符，即空格（space的ASCII为32）
}
printf("\n");
}
printf("\n");
for (int i = 0; i < 3; ++i)
{
for (int j = 0; j < 3; ++j)
{
printf("%7.4f\x20", *(*(p + i) + j));
//p+i表示a[i]的地址
//"%-7.4f中, '-'表示左对齐(无'-'默认为右对齐)；
//7.4表示这个元素输出时占7列，其中包括4个小数
}
printf("\n");
}
printf("\n");
return 0;
} 运行结果如下：
0.057118 0.124758 0.057118
0.124758 0.272496 0.124758
0.057118 0.124758 0.0571180.0571 0.1248 0.0571
0.1248 0.2725 0.1248
0.0571 0.1248 0.0571
中值滤波
中值滤波对于椒盐噪声的处理特别好，它算是统计排序滤波的一种，中值指的就是领域内像素的统计中值。
数字图像处理中对于中值滤波的描述是：用n*n的中值滤波器去除那些相对于其领域像素更亮或更暗，并且其区域小于
（滤波器区域的一半）的孤立像素集。.....而对较大的像素影响较小。
这段话理解起来是这样：
- 中值滤波只对其亮度明显大于或者小于其他周围像素点的噪声有作用。
- 中值滤波器的大小必须是噪声点尺寸的2倍以上。因为中值定大于或小于一半的像素值。
而椒盐噪声非常符合第1点，所以中值滤波对于椒盐噪声的作用非常明显。
中值滤波与均值滤波对于椒盐噪声滤除作用的对比代码：
#include
#include
#include
#include
#include
using namespace cv;
using namespace std;
//给图像加入椒盐噪声
void salt(Mat& image, int n)
{
for (int k = 0; k < n; k++)
{
int i = rand() % image.cols;
int j = rand() % image.rows;
if (image.channels() == 1)
{ //判断是一个通道
image.at(j, i) = 255;
}
else {
image.at(j, i)[0] = 255;
image.at(j, i)[1] = 255;
image.at(j, i)[2] = 255;
}
}
}
int main()
{
Mat src = Mat::zeros(Size(10, 10), CV_8U);
salt(src, 20);
cout << "椒盐噪声污染之后：\n" << src << endl;
//imshow("椒盐噪声污染之后", src);
Mat median_blur;
medianBlur(src, median_blur, 3);
cout << "中值滤波之后：\n" << median_blur << endl;
//imshow("中值滤波之后", median_blur);
Mat uniform_blur;
blur(src, uniform_blur, Size(3, 3));
cout << "均值滤波之后：\n" << uniform_blur << endl;
//imshow("均值滤波之后", uniform_blur);
//waitKey(0);
return 0;
}
程序运行结果如下：
椒盐噪声污染之后：
[ 0, 0, 0, 0, 255, 0, 0, 0, 0, 0;
0, 255, 0, 0, 0, 0, 0, 0, 0, 0;
0, 0, 255, 0, 0, 255, 0, 0, 0, 255;
0, 0, 255, 0, 0, 0, 0, 0, 0, 0;
0, 255, 255, 0, 0, 255, 0, 0, 0, 255;
0, 0, 0, 0, 0, 255, 0, 0, 255, 0;
0, 255, 0, 0, 0, 0, 0, 255, 0, 0;
0, 255, 0, 0, 0, 0, 0, 0, 0, 0;
0, 255, 0, 0, 0, 0, 0, 0, 255, 0;
0, 0, 0, 0, 0, 0, 0, 255, 0, 0]
中值滤波之后：
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0;
0, 0, 0, 0, 0, 0, 0, 0, 0, 0;
0, 0, 0, 0, 0, 0, 0, 0, 0, 0;
0, 0, 0, 0, 0, 0, 0, 0, 0, 0;
0, 0, 0, 0, 0, 0, 0, 0, 0, 0;
0, 0, 0, 0, 0, 0, 0, 0, 0, 0;
0, 0, 0, 0, 0, 0, 0, 0, 0, 0;
0, 0, 0, 0, 0, 0, 0, 0, 0, 0;
0, 0, 0, 0, 0, 0, 0, 0, 0, 0;
0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
均值滤波之后：
[113, 57, 57, 28, 28, 28, 0, 0, 0, 0;
57, 57, 57, 57, 57, 57, 28, 0, 28, 28;
57, 85, 85, 57, 28, 28, 28, 0, 28, 28;
57, 113, 113, 85, 57, 57, 57, 0, 57, 57;
57, 85, 85, 57, 57, 57, 57, 28, 57, 85;
113, 85, 85, 28, 57, 57, 85, 57, 85, 85;
113, 57, 57, 0, 28, 28, 57, 57, 57, 57;
170, 85, 85, 0, 0, 0, 28, 57, 57, 57;
113, 57, 57, 0, 0, 0, 28, 57, 57, 57;
113, 57, 57, 0, 0, 0, 28, 85, 85, 113]
当然可以明显看到中值滤波比均值滤波的效果好不少。对于实际图像的过滤效果如下：
（a）原图 （b）椒盐噪声污染之后
（c）均值滤波效果
（d）中值滤波效果