一、项目介绍
在此项目中,目的是预测爱荷华州Ames的房价,给定81个特征,描述了房子、面积、土地、基础设施、公共设施等。埃姆斯数据集具有分类和连续特征的良好组合,大小适中,也许最重要的是,它不像其他类似的数据集(如波士顿住房)那样存在潜在的红线或数据输入问题。在这里我将主要讨论PyTorch建模的相关方面,作为一点额外的内容,我还将演示PyTorch中开发的模型的神经元重要性。你可以在PyTorch中尝试不同的网络架构或模型类型。本项目中的重点是方法论,而不是详尽地寻找最佳解决方案。
二、准备工作
为了准备这个项目,我们首先需要下载数据,并通过以下步骤进行一些预处理。
from sklearn.datasets import fetch_openml data = fetch_openml(data_id=42165, as_frame=True)
关于该数据集的完整描述,你可以去该网址查看:https://www.openml.org/d/42165。
查看数据特征
import pandas as pd data_ames = pd.DataFrame(data.data, columns=data.feature_names) data_ames['SalePrice'] = data.target data_ames.info()
下面是DataFrame的信息
RangeIndex: 1460 entries, 0 to 1459 Data columns (total 81 columns): Id 1460 non-null float64 MSSubClass 1460 non-null float64 MSZoning 1460 non-null object LotFrontage 1201 non-null float64 LotArea 1460 non-null float64 Street 1460 non-null object Alley 91 non-null object LotShape 1460 non-null object LandContour 1460 non-null object Utilities 1460 non-null object LotConfig 1460 non-null object LandSlope 1460 non-null object Neighborhood 1460 non-null object Condition1 1460 non-null object Condition2 1460 non-null object BldgType 1460 non-null object HouseStyle 1460 non-null object OverallQual 1460 non-null float64 OverallCond 1460 non-null float64 YearBuilt 1460 non-null float64 YearRemodAdd 1460 non-null float64 RoofStyle 1460 non-null object RoofMatl 1460 non-null object Exterior1st 1460 non-null object Exterior2nd 1460 non-null object MasVnrType 1452 non-null object MasVnrArea 1452 non-null float64 ExterQual 1460 non-null object ExterCond 1460 non-null object Foundation 1460 non-null object BsmtQual 1423 non-null object BsmtCond 1423 non-null object BsmtExposure 1422 non-null object BsmtFinType1 1423 non-null object BsmtFinSF1 1460 non-null float64 BsmtFinType2 1422 non-null object BsmtFinSF2 1460 non-null float64 BsmtUnfSF 1460 non-null float64 TotalBsmtSF 1460 non-null float64 Heating 1460 non-null object HeatingQC 1460 non-null object CentralAir 1460 non-null object Electrical 1459 non-null object 1stFlrSF 1460 non-null float64 2ndFlrSF 1460 non-null float64 LowQualFinSF 1460 non-null float64 GrLivArea 1460 non-null float64 BsmtFullBath 1460 non-null float64 BsmtHalfBath 1460 non-null float64 FullBath 1460 non-null float64 HalfBath 1460 non-null float64 BedroomAbvGr 1460 non-null float64 KitchenAbvGr 1460 non-null float64 KitchenQual 1460 non-null object TotRmsAbvGrd 1460 non-null float64 Functional 1460 non-null object Fireplaces 1460 non-null float64 FireplaceQu 770 non-null object GarageType 1379 non-null object GarageYrBlt 1379 non-null float64 GarageFinish 1379 non-null object GarageCars 1460 non-null float64 GarageArea 1460 non-null float64 GarageQual 1379 non-null object GarageCond 1379 non-null object PavedDrive 1460 non-null object WoodDeckSF 1460 non-null float64 OpenPorchSF 1460 non-null float64 EnclosedPorch 1460 non-null float64 3SsnPorch 1460 non-null float64 ScreenPorch 1460 non-null float64 PoolArea 1460 non-null float64 PoolQC 7 non-null object Fence 281 non-null object MiscFeature 54 non-null object MiscVal 1460 non-null float64 MoSold 1460 non-null float64 YrSold 1460 non-null float64 SaleType 1460 non-null object SaleCondition 1460 non-null object SalePrice 1460 non-null float64 dtypes: float64(38), object(43) memory usage: 924.0+ KB
接下来,我们还将使用一个库,即 captum,它可以检查 PyTorch 模型的特征和神经元重要性。
pip install captum
在做完这些准备工作后,我们来看看如何预测房价。
三、实验过程
3.1数据预处理
在这里,首先要进行数据缩放处理,因为所有的变量都有不同的尺度。分类变量需要转换为数值类型,以便将它们输入到我们的模型中。我们可以选择一热编码,即我们为每个分类因子创建哑变量,或者是序数编码,即我们对所有因子进行编号,并用这些数字替换字符串。我们可以像其他浮动变量一样将虚拟变量送入,而序数编码则需要使用嵌入,即线性神经网络投影,在多维空间中对类别进行重新排序。我们在这里采取嵌入的方式。
import numpy as np
from category_encoders.ordinal import OrdinalEncoder
from sklearn.preprocessing import StandardScaler
num_cols = list(data_ames.select_dtypes(include='float'))
cat_cols = list(data_ames.select_dtypes(include='object'))
ordinal_encoder = OrdinalEncoder().fit(
data_ames[cat_cols]
)
standard_scaler = StandardScaler().fit(
data_ames[num_cols]
)
X = pd.DataFrame(
data=np.column_stack([
ordinal_encoder.transform(data_ames[cat_cols]),
standard_scaler.transform(data_ames[num_cols])
]),
columns=cat_cols + num_cols
)
3.2拆分数据集
在构建模型之前,我们需要将数据拆分为训练集和测试集。在这里,我们添加了一个数值变量的分层。这可以确保不同的部分(其中五个)在训练集和测试集中都以同等的数量包含。
np.random.seed(12)
from sklearn.model_selection import train_test_split
bins = 5
sale_price_bins = pd.qcut(
X['SalePrice'], q=bins, labels=list(range(bins))
)
X_train, X_test, y_train, y_test = train_test_split(
X.drop(columns='SalePrice'),
X['SalePrice'],
random_state=12,
stratify=sale_price_bins
)
3.3构建PyTorch模型
接下来开始建立我们的PyTorch模型。我们将使用PyTorch实现一个具有批量输入的神经网络回归,具体将涉及以下步骤。
- 1. 将数据转换为Torch tensors
- 2. 定义模型结构
- 3. 定义损失标准和优化器。
- 4. 创建一个批次的数据加载器
- 5. 跑步训练
3.3.1.数据转换
首先将数据转换为torch tensors
from torch.autograd import Variable
num_features = list(
set(num_cols) - set(['SalePrice', 'Id'])
)
X_train_num_pt = Variable(
torch.cuda.FloatTensor(
X_train[num_features].values
)
)
X_train_cat_pt = Variable(
torch.cuda.LongTensor(
X_train[cat_cols].values
)
)
y_train_pt = Variable(
torch.cuda.FloatTensor(y_train.values)
).view(-1, 1)
X_test_num_pt = Variable(
torch.cuda.FloatTensor(
X_test[num_features].values
)
)
X_test_cat_pt = Variable(
torch.cuda.LongTensor(
X_test[cat_cols].values
).long()
)
y_test_pt = Variable(
torch.cuda.FloatTensor(y_test.values)
).view(-1, 1)
这可以确保我们将数字和分类数据加载到单独的变量中,类似于NumPy。如果你把数据类型混合在一个变量(数组/矩阵)中,它们就会变成对象。我们希望把数值变量弄成浮点数,把分类变量弄成长(或int),索引我们的类别。我们还将训练集和测试集分开。显然,一个ID变量在模型中不应该是重要的。在最坏的情况下,如果ID与目标有任何相关性,它可能会引入目标泄漏。我们已经把它从这一步的处理中删除了。
3.3.2定义模型架构
class RegressionModel(torch.nn.Module):
def __init__(self, X, num_cols, cat_cols, device=torch.device('cuda'), embed_dim=2, hidden_layer_dim=2, p=0.5):
super(RegressionModel, self).__init__()
self.num_cols = num_cols
self.cat_cols = cat_cols
self.embed_dim = embed_dim
self.hidden_layer_dim = hidden_layer_dim
self.embeddings = [
torch.nn.Embedding(
num_embeddings=len(X[col].unique()),
embedding_dim=embed_dim
).to(device)
for col in cat_cols
]
hidden_dim = len(num_cols) + len(cat_cols) * embed_dim,
# hidden layer
self.hidden = torch.nn.Linear(torch.IntTensor(hidden_dim), hidden_layer_dim).to(device)
self.dropout_layer = torch.nn.Dropout(p=p).to(device)
self.hidden_act = torch.nn.ReLU().to(device)
# output layer
self.output = torch.nn.Linear(hidden_layer_dim, 1).to(device)
def forward(self, num_inputs, cat_inputs):
'''Forward method with two input variables -
numeric and categorical.
'''
cat_x = [
torch.squeeze(embed(cat_inputs[:, i] - 1))
for i, embed in enumerate(self.embeddings)
]
x = torch.cat(cat_x + [num_inputs], dim=1)
x = self.hidden(x)
x = self.dropout_layer(x)
x = self.hidden_act(x)
y_pred = self.output(x)
return y_pred
house_model = RegressionModel(
data_ames, num_features, cat_cols
)
我们在两个线性层(上的激活函数是整流线性单元激活(ReLU)函数。这里需要注意的是,我们不可能将相同的架构(很容易)封装成一个顺序模型,因为分类和数值类型上发生的操作不同。
3.3.3定义损失准则和优化器
接下来,定义损失准则和优化器。我们将均方误差(MSE)作为损失,随机梯度下降作为我们的优化算法。
criterion = torch.nn.MSELoss().to(device) optimizer = torch.optim.SGD(house_model.parameters(), lr=0.001)
3.3.4创建数据加载器
现在,创建一个数据加载器,每次输入一批数据。
data_batch = torch.utils.data.TensorDataset(
X_train_num_pt, X_train_cat_pt, y_train_pt
)
dataloader = torch.utils.data.DataLoader(
data_batch, batch_size=10, shuffle=True
)
我们设置了10个批次的大小,接下来我们可以进行训练了。
3.3.5.训练模型
基本上,我们要在epoch上循环,在每个epoch内推理出性能,计算出误差,优化器根据误差进行调整。这是在没有训练的内循环的情况下,在epochs上的循环。
from tqdm.notebook import trange
train_losses, test_losses = [], []
n_epochs = 30
for epoch in trange(n_epochs):
train_loss, test_loss = 0, 0
# print the errors in training and test:
if epoch % 10 == 0 :
print(
'Epoch: {}/{}\t'.format(epoch, 1000),
'Training Loss: {:.3f}\t'.format(
train_loss / len(dataloader)
),
'Test Loss: {:.3f}'.format(
test_loss / len(dataloader)
)
)
训练是在这个循环里面对所有批次的训练数据进行的。
for (x_train_num_batch,x_train_cat_batch,y_train_batch) in dataloader:
(x_train_num_batch,x_train_cat_batch, y_train_batch) = (
x_train_num_batch.to(device),
x_train_cat_batch.to(device),
y_train_batch.to(device))
pred_ytrain = house_model.forward(x_train_num_batch, x_train_cat_batch)
loss = torch.sqrt(criterion(pred_ytrain, y_train_batch))
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_loss += loss.item()
with torch.no_grad():
house_model.eval()
pred_ytest = house_model.forward(X_test_num_pt, X_test_cat_pt)
test_loss += torch.sqrt(criterion(pred_ytest, y_test_pt))
train_losses.append(train_loss / len(dataloader))
test_losses.append(test_loss / len(dataloader))
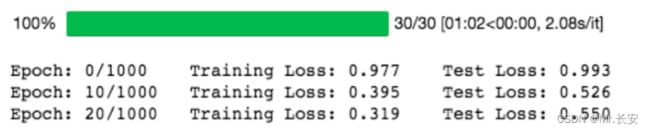
训练结果如下:
我们取 nn.MSELoss 的平方根,因为 PyTorch 中 nn.MSELoss 的定义如下:
((input-target)**2).mean()
绘制一下我们的模型在训练期间对训练和验证数据集的表现。
plt.plot(
np.array(train_losses).reshape((n_epochs, -1)).mean(axis=1),
label='Training loss'
)
plt.plot(
np.array(test_losses).reshape((n_epochs, -1)).mean(axis=1),
label='Validation loss'
)
plt.legend(frameon=False)
plt.xlabel('epochs')
plt.ylabel('MSE')
在我们的验证损失停止下降之前,我们及时停止了训练。我们还可以对目标变量进行排序和bin,并将预测结果与之对比绘制,以便了解模型在整个房价范围内的表现。这是为了避免回归中的情况,尤其是用MSE作为损失,即你只对一个中值范围的预测很好,接近平均值,但对其他任何东西都做得不好。
我们可以看到,事实上,这个模型在整个房价范围内的预测非常接近。事实上,我们得到的Spearman秩相关度约为93%,具有非常高的显著性,这证实了这个模型的表现具有很高的准确性。
四、原理讲解
深度学习神经网络框架使用不同的优化算法。其中流行的有随机梯度下降(SGD)、均方根推进(RMSProp)和自适应矩估计(ADAM)。我们定义了随机梯度下降作为我们的优化算法。另外,我们还可以定义其他优化器。
opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR) opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.6) opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.1) opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.8, 0.98))
SGD的工作原理与梯度下降相同,只是它每次只在一个例子上工作。有趣的是,收敛性与梯度下降相似,并且更容易占用计算机内存。
RMSProp的工作原理是根据梯度符号来调整算法的学习率。最简单的变体是检查最后两个梯度符号,然后调整学习率,如果它们相同,则增加一个分数,如果它们不同,则减少一个分数。
ADAM是最流行的优化器之一。它是一种自适应学习算法,根据梯度的第一和第二时刻改变学习率。
Captum是一个工具,可以帮助我们了解在数据集上学习的神经网络模型的来龙去脉。它可以帮助我们学习以下内容。
- 特征重要性
- 层级重要性
- 神经元的重要性
这在学习可解释的神经网络中是非常重要的。在这里,综合梯度已经被应用于理解特征重要性。之后,还用层传导法来证明神经元的重要性。
五、补充
既然我们已经定义并训练了我们的神经网络,那么让我们使用 captum 库找到重要的特征和神经元。
from captum.attr import (
IntegratedGradients,
LayerConductance,
NeuronConductance
)
house_model.cpu()
for embedding in house_model.embeddings:
embedding.cpu()
house_model.cpu()
ing_house = IntegratedGradients(forward_func=house_model.forward, )
#X_test_cat_pt.requires_grad_()
X_test_num_pt.requires_grad_()
attr, delta = ing_house.attribute(
X_test_num_pt.cpu(),
target=None,
return_convergence_delta=True,
additional_forward_args=X_test_cat_pt.cpu()
)
attr = attr.detach().numpy()
现在,我们有了一个NumPy的特征重要性数组。层和神经元的重要性也可以用这个工具获得。让我们来看看我们第一层的神经元importances。我们可以传递house_model.act1,这是第一层线性层上面的ReLU激活函数。
cond_layer1 = LayerConductance(house_model, house_model.act1) cond_vals = cond_layer1.attribute(X_test, target=None) cond_vals = cond_vals.detach().numpy() df_neuron = pd.DataFrame(data = np.mean(cond_vals, axis=0), columns=['Neuron Importance']) df_neuron['Neuron'] = range(10)
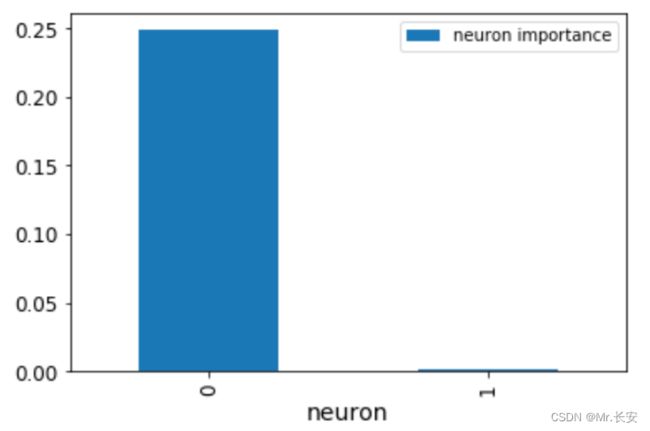
这张图显示了神经元的重要性。显然,一个神经元就是不重要的。我们还可以通过对之前得到的NumPy数组进行排序,看到最重要的变量。
df_feat = pd.DataFrame(np.mean(attr, axis=0), columns=['feature importance'] )
df_feat['features'] = num_features
df_feat.sort_values(
by='feature importance', ascending=False
).head(10)
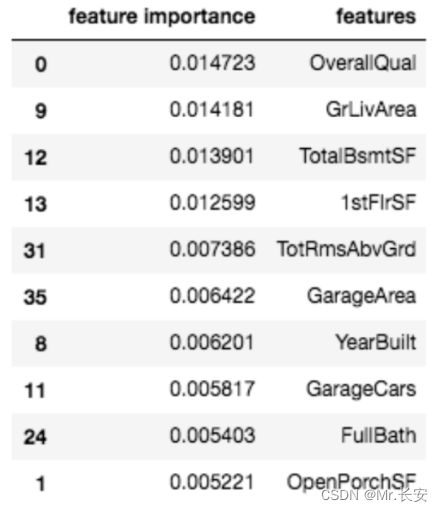
这里列出了10个最重要的变量
通常情况下,特征导入可以帮助我们既理解模型,又修剪我们的模型,使其变得不那么复杂(希望减少过度拟合)。
到此这篇关于如何用Pytorch搭建一个房价预测模型的文章就介绍到这了,更多相关Pytorch房价预测内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!