海王算法（看完不会变成海王）

                                                                  学了海王算法会变成海王吗，它又能解决什么样的问题呢？          

---

仰望天空，妳我亦是行人.✨
个人主页——微风撞见云的博客
数据结构与算法专栏的文章图文并茂生动形象简单易学！欢迎大家来踩踩~
希望本文能够给读者带来一定的帮助文章粗浅，敬请批评指正！

---

---

海王算法的概念

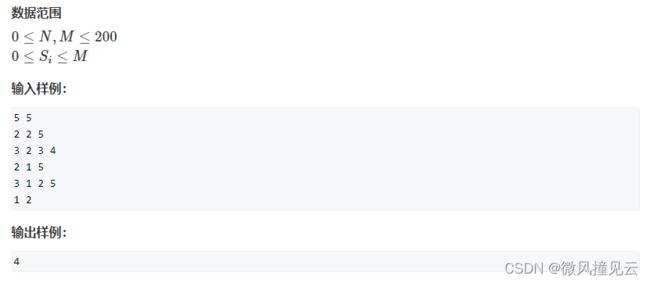
海王算法又叫$匈牙利算法$是由匈牙利数学家Edmonds于1965年提出，因而得名。匈牙利算法是基于Hall定理中充分性证明的思想，它是$部图匹配$最常见的算法，该算法的核心就是$寻找增广路径$，它是一种用增广路径$求二分图最大匹配$的算法。

前景提要

    我个人很喜欢$章若楠$和$许光汉$两位明星，那么，今天我就要来当个媒婆，干啥事儿呢？我要撮合他们，尽量让他们在一起。
    由于我只提到了上面两位明星，那么我就用他们不同的照片来分别作为男一号、男二号、男三号、男四号，女一号、女二号、女三号、女四号，可能有点不太好，但是，我目前觉得还挺好，嘿嘿，就这样吧！

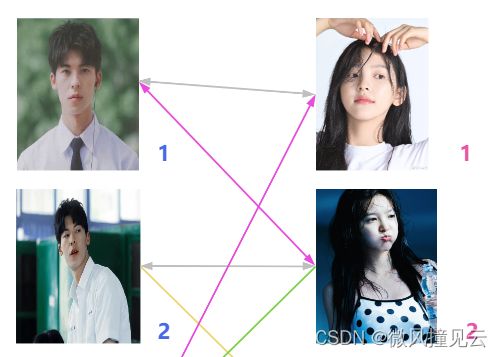
    今天，我是一名伟大的媒婆！我要把男主们和女主们尽最大努力撮合在一起！既然是两个人在一起，那还是得先遵循他们自己的意愿吧。下图中的连线就表示两人相互有好感，也就是说可以尝试在一起一下，我们用个小本本记录一下，看看有哪些连线。（海王算法嘛，当然有海王咯，海王们一般都不专一，一次性喜欢多个人虽然很下头，但还是比较合理的。狗头保命 ）

具体做法

     这个时候，天色骤变，海面上出现了一个$巨大的怪兽$，它咆哮着说：“我就是万恶的$海王$（呜~~~），今天这桩事必须听我的，让我来给他们分配对象，否则我就…”。

    ‍♂️好吧那我们就听它的，看看它能玩出什么花样。

    海王说:“第一步：我先试着给男一号找对象。”

    ‍♂️我给海王说：“我这里有个小本子，上面有他们彼此之间的暧昧关系。”

    海王一看：“好家伙，到底谁是海王？ 这样吧，男一号和女一号都还没确定关系，那我们就先给他们俩搓一对儿吧”。就这样，男一号和女一号暂时牵手成功了。（这里用粉紫色的双向箭头替换原来的连线，表示他们双向奔赴，在一起了。）

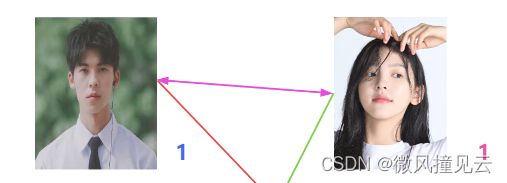
    ‍♂️紧接着，海王发现男二号和女二号也都没有对象，于是给他们俩也安排上了。男二女二暂时牵手成功。

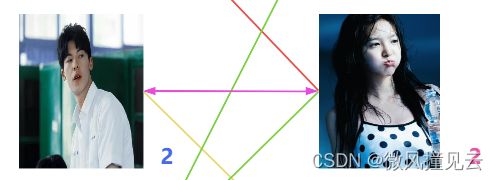
    ‍♂️接下来是男三号，海王发现与男二号有好感的女一号和女二号都已经名花有主了。这可咋办呢？

    海王发话了:“男三号喜欢女一号是吧，那就先把女一号和男一号拆开，重新分配一下。”（用灰色的先表示分手。）

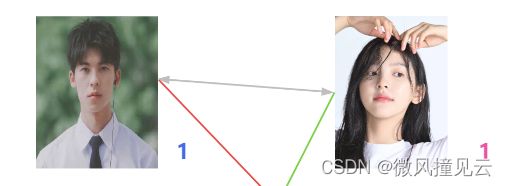
    ‍♂️绝了，什么操作啊？人家手还没牵热乎呢！真不愧是海王，什么事都做得出来！”

    海王：“你少废话，信不信我把你…”

    ‍♂️于是我眼睁睁看着男一号和女一号分开了。男三号和女一号在一起了。那男一号咋办呢？

    海王：“男一号不是还喜欢女二号吗，让他们俩试试。”

    ‍♂️于是男二号和女二号分开了，男一号和女二号在一起了。那男二号咋办呢？

    海王：“男二号不是还喜欢女三号吗，让他们俩试试。”

    ‍♂️于是男二号和女三号在一起了。诶嘿，你别说，你还真别说，虽然海王这样的做法很下头，但是确实多撮合了一对儿出来，还算有点东西。那我们的男四号呢？

    海王看了看小本子说：“这最后一个男生，我按照刚才的转移大法，也不能给他腾个女生出来，毕竟如果我满足了他，那前面的男生总会有一个分手，既然不能多撮合一对儿，那我就省省功力了，放弃这个男生吧。年轻人，我就一个要求，不要做海王，别来和我抢饭碗。后会有期！”

    ‍♂️随着海王的离开，天空也明亮了，太阳格外耀眼，因为我在海王的帮助下，成功撮合了三对暧昧情侣！

    怎么样？看完海王这一顿操作，你悟出了什么道理？没错，有机会要上，别要怂，没机会也要创造机会，尽量撮合更多的暧昧情侣。

    回顾海王的操作，我发现转移大法的精髓就是分配和递归寻找：

    我们需要用以下变量来维护这些操作，它们分别是：

boolean[][] line = new boolean[N][N];//邻接矩阵建立连线
int[] girl = new int[N];//存储每个女生被分配给了哪个男生  girl[1] = 2 --> 1号女生分配给了2号男生
boolean[] used;//这里标记过的意思是这次查找曾试图改变过该妹子的归属问题，但是没有成功，所以就不用瞎费工夫了

find（）

private static boolean find(int x) {
        for (int j = 1; j <= m; j++) {//枚举每个女主
            if (line[x][j] && !used[j]) {//如果有暧昧并且还没有标记过
                used[j] = true;
                if (girl[j] == 0 || find(girl[j])) {//名花无主 或者 能腾出个位置来【递归实现】
                    girl[j] = x;
                    return true;
                }
            }
        }
        return false;
    }

在主函数这样做

 //看看能否给男生i分配一个女生
        for (int i = 1; i <= n; i++) {
            used = new boolean[N];//每次都给他new个新的，目的就是重置状态
            if (find(i)) ans++;
        }

暧昧情侣代码如下：

public class 暧昧情侣 {
    static int N = (int) 1e4 + 10;
    static boolean[][] line = new boolean[N][N];//邻接矩阵建立连线
    static int[] girl = new int[N];//存储每个女生被分配给了哪个男生  girl[1] = 2 --> 1号女生分配给了2号男生
    static boolean[] used;//这里标记过的意思是这次查找曾试图改变过该妹子的归属问题，但是没有成功，所以就不用瞎费工夫了
    static int n, m, ans;
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    public static void main(String[] args) throws IOException {
        in.nextToken();
        n = (int) in.nval;//男
        in.nextToken();
        m = (int) in.nval;//女
        in.nextToken();
        int k = (int) in.nval;//k条记录，表示男女之间彼此之间有好感
        int temp;
        while (k-- > 0) {
            in.nextToken();
            temp = (int) in.nval;
            in.nextToken();
            line[temp][(int) in.nval] = true;
        }
        //看看能否给男生i分配一个女生
        for (int i = 1; i <= n; i++) {
            used = new boolean[N];
            if (find(i)) ans++;
        }
        System.out.println(ans);
    }

    private static boolean find(int x) {
        for (int j = 1; j <= m; j++) {//枚举每个妹子
            if (line[x][j] && !used[j]) {//如果有暧昧并且还没有标记过
                used[j] = true;
                if (girl[j] == 0 || find(girl[j])) {//名花无主 或者 能腾出个位置来【递归实现】
                    girl[j] = x;
                    return true;
                }
            }
        }
        return false;
    }
}

相关解释：

/**
*find(3), x=3, j=1, girl[j]=1（女士1已暂时被许配给了男士1）->find(girl[j])(进入递归，看能不能给男士1>再找个对象，把女士1让出来给男士3)，
*find(1), used[1]=1,所以跳过j=1，进入j=2(男士1也很欣赏女士2),girl[j]=2(但女士2已暂时被许配给了男>士2) ->
*-> find(girl[j])(进入递归，看能不能给男士2再找个对象，把女士2让出来给男士1),
*find(2), used[2]=true,跳过j=1,j=2，进入j=3(男士2也很欣赏女士3)，girl[j]=0(女士3单身)， 正好，>girl[j]=2（女士3许配给男士2），return true，
*此时回溯到上一步find(1)这里面，既然find(girl[j])=True（给男士2重新找了个对象女士3）了，>girl[j]=1(女士2恢复单身了，和男士1在一起了)，return true
*此时再回溯到上上一步find(3)这里面，既然find(girl[j])=True（给男士1找到了新对象女士2），girl[j]=3>（女士1恢复单身了，和男士3在一起了），return true
*
*至此由男士3单身引起的一系列递归和回溯结束了，并凑成了三对情侣。
*再回到大循环下，继续向下执行就好了
*/

巩固加深

题目：完美牛棚

邻接矩阵解法

import java.io.*;
import java.util.Arrays;

public class Main {
    static int N = 210;
    static boolean[][] line = new boolean[N][N];
    static int[] match = new int[N];
    static boolean[] vis = new boolean[N];
    static int n, m;
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    public static void main(String[] args) throws IOException {
        in.nextToken();
        n = (int) in.nval;//牛
        in.nextToken();
        m = (int) in.nval;//棚
        for (int i = 1; i <= n; i++) {
            int count;
            in.nextToken();
            count = (int) in.nval;
            while (count-- > 0) {
                in.nextToken();
                line[i][(int) in.nval] = true;
            }
        }
        int res = 0;
        for (int i = 1; i <= n; i++) {
            Arrays.fill(vis, false);
            if (find(i)) res++;
        }
        System.out.println(res);
    }

    private static boolean find(int x) {
        for (int i = 1; i <= m; i++) {
            if (!vis[i] && line[x][i]) {
                vis[i] = true;
                if (match[i] == 0 || find(match[i])) {
                    match[i] = x;
                    return true;
                }
            }
        }
        return false;
    }
}

链式前向星解法

import java.io.*;
import java.util.Arrays;

public class Main {
    static int N = 210, M = N * N;//注意：最多有N * N条边
    static int[] match = new int[N];
    static boolean[] vis = new boolean[N];
    static int n, m;
    static int total;//第n条边，从1开始
    static int[] head = new int[M], next = new int[M], ends = new int[M];//这里不需要考虑边权
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    static void add(int start, int end) {
        ends[++total] = end;
        next[total] = head[start];
        head[start] = total;
    }

    public static void main(String[] args) throws IOException {
        in.nextToken();
        n = (int) in.nval;//牛
        in.nextToken();
        m = (int) in.nval;//棚
        Arrays.fill(head, -1);
        for (int i = 1; i <= n; i++) {
            in.nextToken();
            int count = (int) in.nval;
            while (count-- > 0) {
                in.nextToken();
                add(i, (int) in.nval);
            }
        }
        int res = 0;
        for (int i = 1; i <= n; i++) {
            Arrays.fill(vis, false);
            if (find(i)) res++;
        }
        System.out.println(res);
    }

    private static boolean find(int x) {
        for (int i = head[x]; i != -1; i = next[i]) {
            int j = ends[i];
            if (!vis[j]) {
                vis[j] = true;
                if (match[j] == 0 || find(match[j])) {
                    match[j] = x;
                    return true;
                }
            }
        }
        return false;
    }
}

---

结语

初学一门技术时，总有些许的疑惑，别怕，它们是我们学习路上的点点繁星，帮助我们不断成长。

文章粗浅，希望对大家有帮助！

参考文章：趣写算法系列之–匈牙利算法