Dijikstra与Floyd两种最短路径算法的解析与Golang代码实现

1.Dijikstra算法理论

​ 在一个带权图中，从某一个单源节点，走到其他节点，如何求得所有路径中的最短路径，是单元节点最短路径问题。而在路由算法中，与此类似，可以抽象出该模型来。迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的。是从一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

Ø 基本思想

​ 通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是”起点s到该顶点的路径”。然后，从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 … 重复该操作，直到遍历完所有顶点。

Ø 操作步骤

​ \1. 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为”起点s到该顶点的距离”[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。

\2. 从U中选出”距离最短的顶点k”，并将顶点k加入到S中；同时，从U中移除顶点k。

\3. 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。

\4. 重复步骤(2)和(3)，直到遍历完所有顶点。

Ø 图解

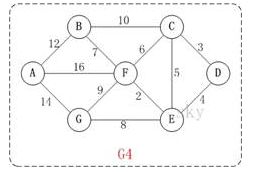
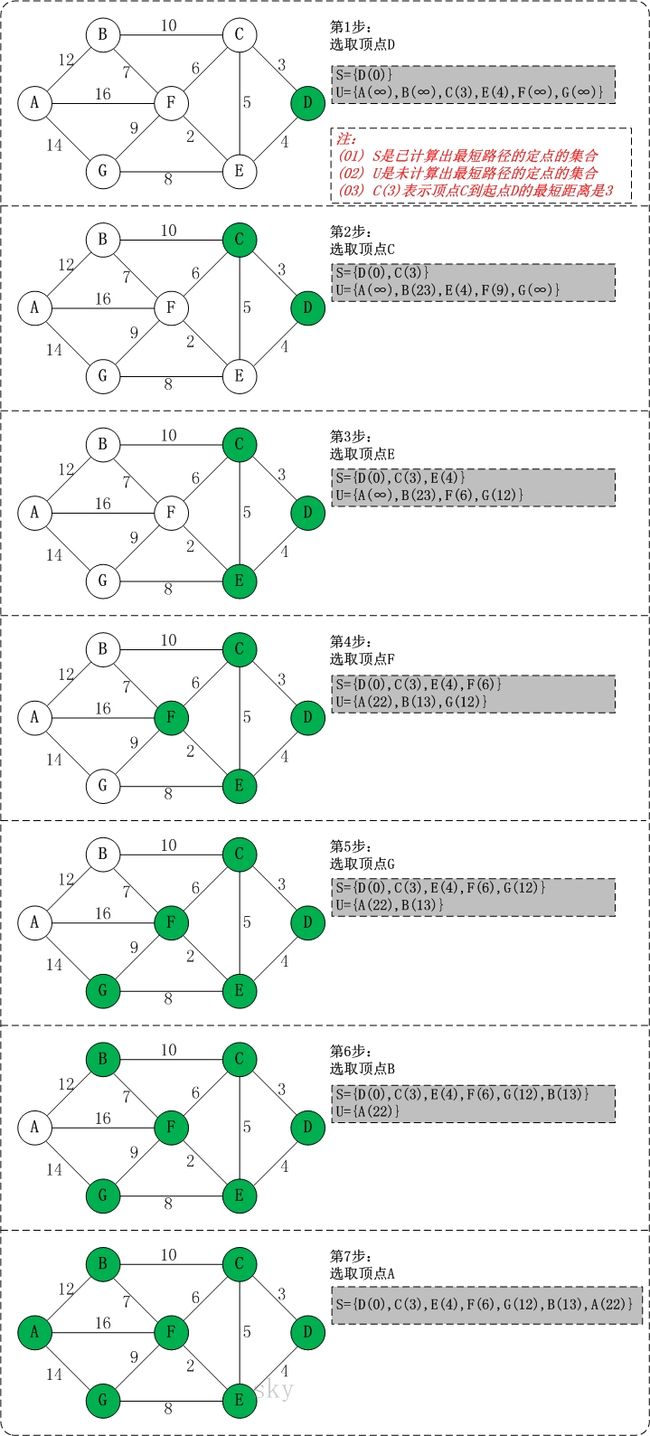
以上图G4为例，来对迪杰斯特拉进行算法演示(以第4个顶点D为起点)。以下B节点中23应为13。

初始状态：S是已计算出最短路径的顶点集合，U是未计算除最短路径的顶点的集合！

第1步：将顶点D加入到S中。

此时，S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。

第2步：将顶点C加入到S中。

上一步操作之后，U中顶点C到起点D的距离最短；因此，将C加入到S中，同时更新U中顶点的距离。以顶点F为例，之前F到D的距离为∞；但是将C加入到S之后，F到D的距离为9=(F,C)+(C,D)。

此时，S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。

第3步：将顶点E加入到S中。

上一步操作之后，U中顶点E到起点D的距离最短；因此，将E加入到S中，同时更新U中顶点的距离。还是以顶点F为例，之前F到D的距离为9；但是将E加入到S之后，F到D的距离为6=(F,E)+(E,D)。

此时，S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。

第4步：将顶点F加入到S中。

此时，S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。

第5步：将顶点G加入到S中。

此时，S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。

第6步：将顶点B加入到S中。

此时，S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。

第7步：将顶点A加入到S中。

此时，S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。

此时，起点D到各个顶点的最短距离就计算出来了：A(22) B(13) C(3) D(0) E(4) F(6) G(12)。

2.Dijikstra算法的Golang实现

func Dijkstra_Alg(D [LEN][LEN]int, v int)  {
   if v < 0 || v >= LEN{
      fmt.Println("错误节点输入！")
      return
   }
   //替换一些原数组中的-1
   for i:=0; i<LEN; i++ {
      for j:=0; j<LEN; j++ {
         if D[i][j] == -1{
            D[i][j] = 9999999
         }
      }
   }
   //1. 创建S集合
   S := make([]int, 0)
   S = append(S, v)
   //2. 对于当前顶点，做一次迪杰斯特拉算法
   //看邻接表对应的那一列
   for {
      //2.1 找出当前列最小加入到S, 要排除掉已经在S中的点
      min := 9999999
      index := v
      for i:=0; i<LEN; i++{
         if !Contains(S, i) && D[i][v] < min{
            min = D[i][v]
            index = i
         }
      }
      //填充之前判断一下，防止后面都是无穷大
      if min == 9999999 && index == v{
         break     //如果最小的都是∞那么说明后面没有点可以加入了，所以结束
      }
      fmt.Printf("最小值min=%d, 加入节点%d \n", min, index)
      S = append(S, index)   //加入目前最小的到S中
      //2.2 根据先加入的这个点,更新其他点的权重
      for i:=0; i<LEN; i++ {
         if !Contains(S, i) && D[i][index] + min < D[i][v]{
            D[i][v] = D[i][index] + min
         }
      }
      fmt.Println("集合S:", S)
      //2.3 检测下S是否满了，满了就退出，不满就重复前两步
      if len(S) >= LEN{
         break
      }
      fmt.Println("===============================")
   }

   //输出数组看一下
   fmt.Println("-----------------Dijkstra算法结果-----------------")
   fmt.Println(S)
   fmt.Println("-----------------最短路径：-----------------")
   fmt.Printf("点%d到各个点的最短路长度是:\n", v)
   for i:=0; i<len(S); i++ {
      fmt.Printf("(%d, %d) = %d \n", v, S[i], D[S[i]][v])
   }
}

程序测试运行结果：

3.Floyd算法理论

​ Floyd算法又称为插点法，是一种用于寻找给定的加权图中多源点之间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。从图的带权邻接矩阵A=[a(i,j)] n×n开始，递归地进行n次更新，即由矩阵D(0)=A，按一个公式，构造出矩阵D(1)；又用同样地公式由D(1)构造出D(2)；……；最后又用同样的公式由D(n-1)构造出矩阵D(n)。矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度，称D(n)为图的距离矩阵，同时还可引入一个后继节点矩阵path来记录两点间的最短路径。采用松弛技术（松弛操作），对在i和j之间的所有其他点进行一次松弛。所以时间复杂度为O(n^3)。

其核心思想是，通过三重嵌套循环，每次选取一个节点去作为中间过渡节点，判断其他任意两对节点间，如果通过所选取的节点来过渡，得到的路径长度较短，则更新该对节点之间的路径距离，即更新所对应的的距离矩阵的数值，这样最外层循环控制的是所选取的节点作为更新节点，内部嵌套的两个循环是作为遍历选取任意两个节点，来判断是否通过所选取的中间节点来过渡得到的距离更短，这样最外层循环，每一次进行下一步，距离举证将会得到更新，即Warshall方法中所对应的的矩阵更新变化。

优点：容易理解，可以算出任意两个节点之间的最短距离，代码编写简单。

缺点：时间复杂度比较高，不适合计算大量数据。

4.Floyd算法Go编程实现

func Floyd_Alg(D [LEN][LEN]int)  {
   //1. 创建对应的Path矩阵
   //1.1 输出原邻接矩阵
   fmt.Println("--------------------原来的邻接矩阵--------------------")
   PrintMatrix(D[:])
   //1.2 创建Path数组
   var Path [LEN][LEN]int
   for i:=0; i<LEN; i++ {
      for j:=0; j<LEN; j++ {
         Path[i][j] = -1
      }
   }
   //2. 处理下原邻接矩阵的-1，不影响下面的判断
   for i:=0; i<LEN; i++ {
      for j:=0; j<LEN; j++ {
         if D[i][j] == -1{
            D[i][j] = 9999999
         }
      }
   }
   //3. 三层循环更新原邻接矩阵和Path矩阵
   for v:=0; v<LEN; v++ {
      for i:=0; i<LEN; i++ {
         for j:=0; j<LEN; j++ {
            //制造全排列
            if i == j ||  v == j || v == i{
               //三者不能相等，相等则跳过
               continue
            }
            //fmt.Printf("V:%d, (%d, %d)\n", v, i, j)

            //如果加上中间点，可以减小距离,那么就更新两个表
            if D[i][j] > D[i][v] + D[v][j] {
               D[i][j] = D[i][v] + D[v][j]    //更新原邻接矩阵
               Path[i][j] = v //更新Path路径图
            }
         }
      }
   }
   //4. 输出邻接矩阵和没两个点之间的最短路径
   fmt.Println("--------------------Floyd求得的最短距离邻接矩阵--------------------")
   PrintMatrix(D[:])
   fmt.Println("-----------------------------------------------------------------")
   fmt.Println(D)
   //输出每两个点的最短路径
   for i:=0; i<LEN; i++ {
      for j:=0; j<LEN; j++ {
         if i == j {
            continue
         }
         fmt.Printf("(%d, %d)点%d到点%d的最短路径是：", i, j, i, j)
         PrintPathMatrix(Path[:], i, j)
         fmt.Printf("\n")
      }
   }
}

运行结果截图：

5.最短路径算法总结

​ 两种方法的时间复杂度都是N的三次方，均不适合大量数据的计算，比较的来看，Dijkstra算法和Floyd算法的思想都是“贪心”的思想，而Floyd算法的最短路径输出则是使用了递归的思想。Dijkstra算法每次只能求得单个点到其他点的最短路径，而Floyd算法则一次性可以求出每个点之间的最短路径，以上就是两个算法的异同。

参考资料

CSDN：

https://blog.csdn.net/heroacool/article/details/51014824

https://www.cnblogs.com/skywang12345/p/3711512.html

https://blog.csdn.net/wang_dong001/article/details/50196103