在python中使用最小二乘法画出拟合曲线_基于jupyter notebook的python编程-----运用最小二乘法,导入文件数据模拟一元线性回归分析...
基于jupyter notebook的python编程-----运用最小二乘法,导入文件数据模拟一元线性回归分析
用最小二乘法模拟一元线性回去曲线的目录
一、运行jupyter notebook,搭建python环境
1、打开Windows终端命令行,输入==jupyter notebook==,打开我们的jupyter工具,如下所示:
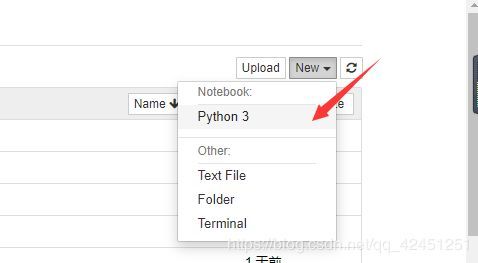
2、在jupyter的web网页中创建python文件,如下所示:
3、现在就可以在jupyter的代码行里面输入我们的代码啦!
二、以下列的csv文件为例,编写我们的最小二乘法的python代码的分解步骤
1、导入我们需要的基本库
2、导入我们数据文件==mytest.csv==
3、为我们的x,y赋值采样
4、下面就是我们最小二乘法的算法编写,求y=ax+b中的==a==和==b==
5、输出打印我们求出的线性回归方程
6、通过==scatter==画出拟合曲线图
三、python最小二乘法的全部源码
四、==shift+enter==运行我们的代码
1、运行结果如下图所示:
2、可以看出,以上是我们通过python代码拟合的自变量X(体重)取值20个的线性回归方程,接下来我们通过wps的excel对同样的数据,同样的20个取值,与我们最小二乘法的结果对比,如下图所示:
3、给出自变量X取值200个和2000个的线性回归方程,大家可以自己修改x,y赋值来做!
**在进行人工智能与机器学习的时候,线性回归是我们必须经历的一步,而利用最小二乘法模拟线性回归分析是基础,本次博客,我们将学习
如何利用最小二乘法,导入文件数据,进行线性回归的模拟!**
一、运行jupyter notebook,搭建python环境
1、打开Windows终端命令行,输入jupyter notebook,打开我们的jupyter工具,如下所示:
2、在jupyter的web网页中创建python文件,如下所示:
3、现在就可以在jupyter的代码行里面输入我们的代码啦!
二、以下列的csv文件为例,编写我们的最小二乘法的python代码的分解步骤
![]()
文件内容如下:
文件中为体重X,身高Y的线性回归关系
1、导入我们需要的基本库
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
2、导入我们数据文件mytest.csv
points = np.genfromtxt("D:/mytest.csv",delimiter=",")
#print(points)#输入我们文件内容,这里注释掉,有想看文件内容的小伙伴可以去掉注释,打印出来!
3、为我们的x,y赋值采样
x=points[0:20,1];
y=points[0:20,2];
以上的代码的含义是:
自变量x的取值为0~20行,第2列的数据,也就是我们的体重
因变量y的取值为0~20行,第3列的数据,也就是我们的身高
如下图:
上述表示,我们只取前20行的数据进行线性回归的拟合,举一反三,如果我们需要取200行,200行,我们就可以如下所示修改:
1)、前200行数据的x,y赋值
x=points[0:200,1];
y=points[0:200,2];
2)、前2000行数据的x,y赋值
x=points[0:2000,1];
y=points[0:2000,2];
4、下面就是我们最小二乘法的算法编写,求y=ax+b中的a和b
x_mean = np.mean(x)
y_mean = np.mean(y)
xsize = x.size
zi = (x * y).sum() - xsize * x_mean *y_mean
mu = (x ** 2).sum() - xsize * x_mean ** 2
# 参数a b
a = zi / mu
b = y_mean - a * x_mean
# 这里对参数保留两位有效数字
a = np.around(a,decimals=2)
b = np.around(b,decimals=2)
那么,以上的公式是怎么来的呢?这就要用到我们最小二乘法计算线性回归的计算公式,如下:
以上的python算法就来自这个公式,最后结果只保留两位有效数字哦!
5、输出打印我们求出的线性回归方程
print(f'回归线方程:y = {a}x + {b}')
6、通过scatter画出拟合曲线图
#借助第三方库skleran画出拟合曲线
y1 = a*x + b
plt.scatter(x,y)
plt.plot(x,y1,c='r')
以上就是我们通过最小二乘法进行一元线性回归模拟的全部过程,比较简单,应该都可以理解!
三、python最小二乘法的全部源码
#用jupyter编程(不借助第三方库),用最小二乘法,
#当体重X变量取20个的时候
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
points = np.genfromtxt("D:/mytest.csv",delimiter=",")
#points
#提取points中的两列数据,分别作为x,y
# 回归方程y = ax + b 求a 和 b
x=points[0:20,1];
y=points[0:20,2];
x_mean = np.mean(x)
y_mean = np.mean(y)
xsize = x.size
zi = (x * y).sum() - xsize * x_mean *y_mean
mu = (x ** 2).sum() - xsize * x_mean ** 2
# 参数a b
a = zi / mu
b = y_mean - a * x_mean
# 这里对参数保留两位有效数字
a = np.around(a,decimals=2)
b = np.around(b,decimals=2)
print(f'回归线方程:y = {a}x + {b}')
#借助第三方库skleran画出拟合曲线
y1 = a*x + b
plt.scatter(x,y)
plt.plot(x,y1,c='r')
四、shift+enter运行我们的代码
1、运行结果如下图所示:
2、可以看出,以上是我们通过python代码拟合的自变量X(体重)取值20个的线性回归方程,接下来我们通过wps的excel对同样的数据,同样的20个取值,与我们最小二乘法的结果对比,如下图所示:
可以看出,python拟合出来的线性回归和我们excel拟合的线性回归的方程,大致一样,就是有效数字的问题,可以看出,我们编写的代码还是比较完美的!
3、给出自变量X取值200个和2000个的线性回归方程,大家可以自己修改x,y赋值来做!
1)、取值200个x
对比excel:
2)、取值2000个x
对比excel:
以上就是我们本次博客的全部内容,希望通过本次博客,大家可以更好的理解最小二乘法求线性回归方程哦!
遇到问题的小伙伴评论区留言哦,学长给你们耐心解答!
陈一月的又一天编程岁月^ _ ^