大规模数据量下ES如何实现高性能检索?
大规模数据量下ES如何实现高性能检索?
- 写在前面
- 倒排索引
- Term Index 的组织形式
- 使用FST压缩Term Index
- 使用Frames of Reference 压缩 Posting List
- 使用Roaring Bitmaps缓存常用filter查询的结果
- 通过对Posting List取交集实现联合索引
- 总结
写在前面
ElasticSearch,是基于Lucene库的搜索引擎。它提供了一个分布式、多租户的全文搜索引擎,具有HTTP web接口和无模式JSON文档。根据DB引擎排名,Elasticsearch是最受欢迎的企业搜索引擎。ES的特点是分布式、高扩展以及近实时。那么,大规模数据量下ES是如何实现高性能检索的呢?
倒排索引
说到ES,就不得不说倒排索引了。我们平时通过ES进行模糊查询,其底层原理就依赖于倒排索引。
首先来介绍一下正向索引与倒排索引的区别:
- 正向索引:用户发起查询时(假设查询为一个关键词),搜索引擎会依次扫描索引库中的所有文档,找出所有包含该关键词的文档。
- 倒排索引:用户发起查询时(假设查询为一个关键词),搜索引擎会在关键词到文档id的映射中,找到所有包含该关键词的文档id,然后找到对应的文档。
假设需要对下面两个工地的信息进行倒排索引的创建:
- 文档id为001,工地名称为“北京海淀花园小区”;
- 文档id为002,工地名称为“北京朝阳星空小区”。
首先,ES将文档交给分析器进行处理,处理的过程包括字符过滤、分词和分词过滤,最终的处理结果是文档内容被表示为一系列关键词信息(关键词本身以及它在文档中出现的位置信息和词性信息)的集合。如下图所示。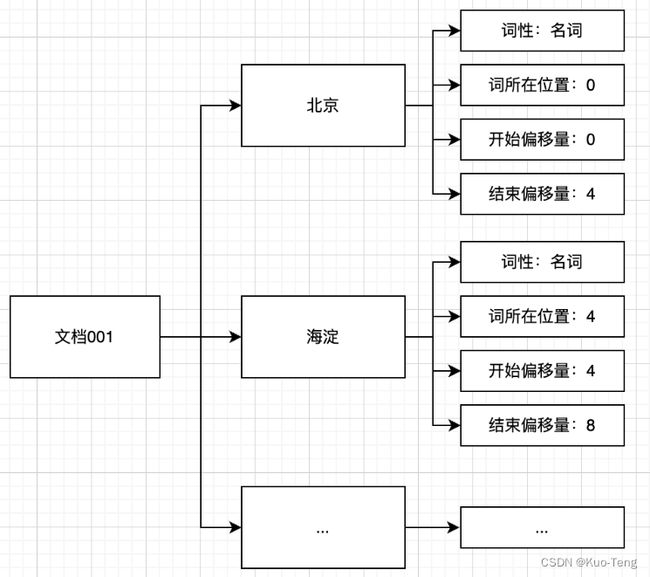
其次,ES根据分析结果建立文档-词语矩阵,用以表示词语和文档的包含关系,如图所示。
文档-词语矩阵建立完成之后,接着需要建立基于词语的倒排索引。ES会遍历文档词语矩阵中的每一个词语,然后将包含该词语的文档信息与该词语建立一种映射关系。映射关系中的词语集合叫作Term Dictionary。映射中的文档集合信息不仅包含文档id,还包含词语在文档中的位置和词频信息,包含这些文档信息的结构叫作Posting List。对于一个规模很大的文档集合来说,可能包含几十万甚至上百万的词语集合,能否快速定位某个词语,直接影响搜索时的响应速度。因此需要一种高效的数据结构对映射关系中的词语集合进行索引,这种结构叫作Term Index。上述3种结构结合在一起就构成了ES的倒排索引结构,逻辑关系如图所示。
本例中的倒排索引结构如图所示。
Term Index 的组织形式
在前一小节我们说到,需要一种高效的数据结构对映射关系中的词语集合也就是Term Dictionary进行索引,这种结构叫作Term Index。那么,Term Index是以怎样的形式进行组织的呢?
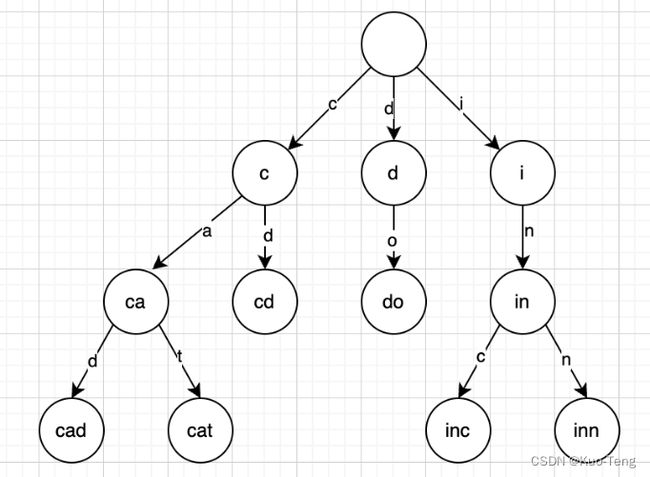
最简单的理解,Term Index就像一本词典的目录一样,但是实际上Term可以是任意的byte数组,而不仅仅是英文字符,因此实际的Term Index是一棵Trie Tree:
这棵Trie Tree不会包含所有的term,它包含的是term的一些前缀。通过Term Index可以快速地定位到Term Dictionary的某个offset,然后从这个位置再往后顺序查找。再加上一些压缩技术比如FST,Term Index需要的存储空间非常小,可能只有所有term占用空间的几十分之一,因此Term Index被完全缓存在内存中是没有问题的。
使用了Term Index后,ES的倒排索引整体效果如下:
在数据量比较大的情况下,如果在MySQL中想要检索到一条记录,即使建立了索引,但索引是以B+ Tree的形式存储在磁盘上的,因此需要若干次的random access的磁盘操作。而ES在Term Dictionary(相当于MySQL中的索引)的基础上,又添加了Term Index这一结构,并且直接以Trie Tree的形式缓存在内存中。在检索一个term时,只需要从Term Index查找到对应的Term Dictionary的block的位置,再到磁盘上去访问对应的数据,大大减少了对磁盘的random access操作的次数。因此我们可以说,在数据量比较大的情况下,ES的检索比MySQL快得多。
使用FST压缩Term Index
在前一小节我们说到,Term Index要被直接缓存在内存中以提升查找速度,那么就必然要采用某种结构来压缩Term Index。Term Index在内存中就是以FST(Finite State Transducers,有限状态转换机)的形式来存储的。FST相对于Trie Tree来说,唯一的不同是Trie Tree只共享了前缀,而FST不仅共享了前缀,也共享了后缀。FST的数据结构可以理解成key -> value的形式,其中key是term,value是对应的Term Dictionary的block的位置。经典FST算法要求key必须按照字典序从小到大加入到FST中。
FST具有两大优点:
- 空间占用小:通过对前缀和后缀的重复利用,压缩了存储空间;
- 查询速度快:时间复杂度为O(len(str));
说到FST,就不得不提FSM(Finite State Machines,有限状态机):表示有限个状态集合以及这些状态之间转移和动作的数学模型。其中一个状态被标记为开始状态,0个或多个状态被标记为final状态。一个FSM同一时间只处于一个状态。
在图中,椭圆形中代表的是状态,而箭头则代表了转移。图中这个FSM代表了对人的一天之内活动的一个抽象,但是未标注开始状态与结束状态。人在同一时间只能处于一种状态,并且从一个状态转移到下一个状态需要一个输入。如果在这个FSM中,人的初始状态为“睡觉”,然后接收的输入依次为:睡醒了、吃饱了、累了、有新电影上映、困了,那么这个人的状态就会依次变化:睡觉 → 吃饭 → 工作 → 逛街 → 睡觉。
前面说到,FST的数据结构可以理解成key -> value的形式,且经典FST算法要求key必须按照字典序从小到大加入到FST中,因此FST其实是一种Ordered Map结构,其key是有序的。
为了方便理解,我们先使用一个DAFSA(Deterministric Acyclic Finite State Acceptor,确定无环有限状态接收机)来实现一个Ordered Set。然后在此基础上,再使用FST来实现一个Ordered Map。
DAFSA的特性如下:
- 确定:意味着指定任何一个状态,只可能最多有一个转移可以访问到;
- 无环: 不可能重复遍历同一个状态;
- 接收机:有限状态机只“接受”特定的输入序列,并终止于final状态;
如果只有一个元素:“bei”,DAFSA是这样的: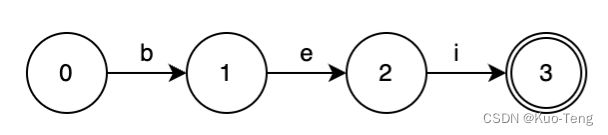
如果要查询“bei”是否属于该集合,只需要按照字符依次输入:
- 输入”b“,DAFSA的状态从0到1;
- 输入”e“,DAFSA的状态从1到2;
- 输入”i“,DAFSA的状态从2到3;
这时,该DAFSA已经到达final状态3,因此“bei”是属于该集合的;
如果要查询“bao”是否处于该集合,在输入“a”的时候,DAFSA会在状态1无法继续移动,因此可以判断”bao“不属于该集合;
查找某个key是否存在于该集合中的时间复杂度为O(length(key));
现在我们往这个DAFSA里面再添加一个元素:”kay“,DAFSA会变成这样: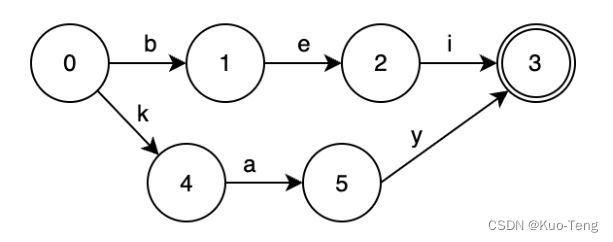
start状态0此时有了两个转移:“b”和“k”。
接下来我们再看一下由“october“,“november“和”december“构成的DAFSA:
其中,“october“,“november“和”december“共有的后缀“ber”在DAFSA中只出现了一次;“november“和”december“共有的后缀“ember”在DAFSA中也只出现了一次;
接下来,我们用一个DAFST(Deterministric Acyclic Finite State Transducer,确定无环有限状态转换器)来实现一个Ordered Map。DAFST的特性如下:
- 确定:意味着指定任何一个状态,只可能最多有一个转移可以访问到;
- 无环: 不可能重复遍历同一个状态;
- 转换器:接受特定的输入序列,终止于final状态,同时会输出一个值;
DAFST与DAFSA的区别在于,对于一个指定的key,DAFST不仅可以判断其是否存在,还可以输出一个与之关联的value,因此可以用于构建一个Ordered Map。
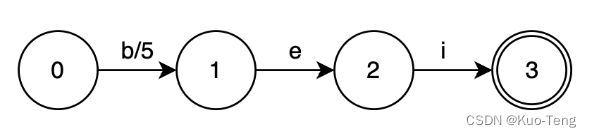
如果只有一个元素:“bei”,其对应的value为5,DAFST是这样的:
如果要查询“bei”,只需要按照字符依次输入:
- 输入”b“,DAFST的状态从0到1,value = 5;
- 输入”e“,DAFST的状态从1到2,value = 5 + 0 = 5;
- 输入”i“,DAFST的状态从2到3,value = 5 + 0 = 5;
这时,该DAFST已经到达final状态3,因此“bei”是属于该集合的,且对应的value为5;
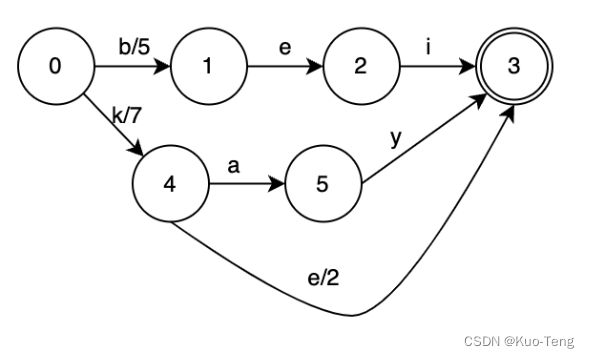
现在我们往这个DAFST里面再添加一个元素:”kay“,其对应value为7,DAFST会变成这样: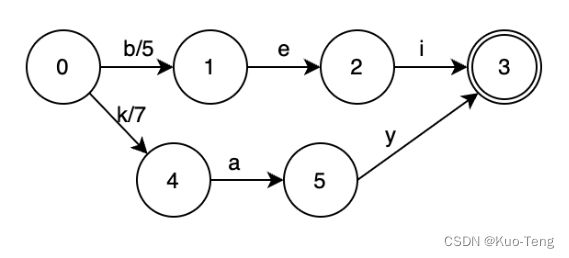
如果我们再添加一个元素“ke",其对应value为9,DAFST会变成这样:
我们可以发现,状态4到状态3,多了一个转移“e”,其weight为2;这样就可以使“kay”和“ke“共用从状态0经过转移“k”到状态4的weight,同时保证能够分别找到自己的正确的值。
建立FST之后,就可以很轻松地根据一个key找到对应的value了。例如:查找“kay”,我们查找的路径为:0 → 4 → 5 → 3,“kay”这个term对应的Term Dictionary的block的位置就是7 + 0 + 0 = 7;
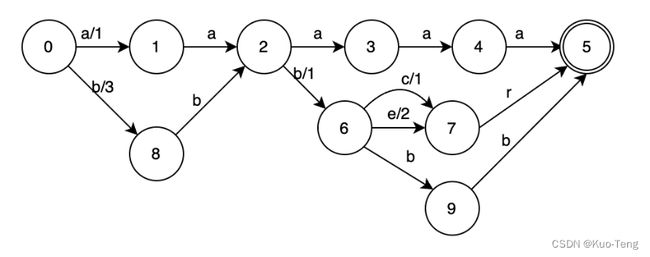
再举一个FST同时复用前缀和后缀的例子:
我们按照如下的key -> value构建一个如下的FST:
- “aaaaa” -> 1
- “aaber” -> 2
- “bbaaa” -> 3
- “bbbbb” -> 4
- “bbbcr” -> 5
- “bbber” -> 6
可以看到,“aaaaa”对应的转移路径为:0 -> 1 -> 2 -> 3 -> 4 -> 5,对应的value为1 + 0 + 0 + 0 + 0 = 1;
“bbbcr”对应的转移路径为:0 -> 8 -> 2 -> 6 -> 7 -> 5,对应的value为:3 + 0 + 1 + 1 + 0 = 5;
“bbber”对应的转移路径同样为:0 -> 8 -> 2 -> 6 -> 7 -> 5,但是在6 -> 7是,走的转移为“e”,对应的value为:3 + 0 + 1 + 2 + 0 = 6;
因此,ES通过使用FST对Term Index进行前缀和后缀的重复利用,在最大限度上降低了检索的时间复杂度和空间复杂度,查找某个key的时间复杂度为O(length(key));
使用Frames of Reference 压缩 Posting List
Elasticsearch里除了用FST压缩Term Index外,对Posting List也有压缩技巧。 可能有同学会问了,Posting List不是已经只存储文档id和offset这些信息了吗?应该已经很小了呀?还需要压缩?让我们试想一下,如果Elasticsearch需要对同学的性别进行索引会怎样?如果有上千万个同学,而只有“男/女“这样两个性别,每个Posting List都会至少包含数百万个文档id。 这时候是不是需要压缩了呢?
那么Elasticsearch是如何有效地对这些文档id压缩的呢?
答案是Frames Of Reference。
比如,文档列表包含[73, 300, 302, 332, 343, 372],经过Delta-encode之后,得到[73, 227, 2, 30, 11, 29]。Lucene用的就是这个技术,会对Posting List中的文档id进行编码,将每256个文档id分成一组,每个组分别使用Delta-encode压缩,然后计算该组中每个数字所需要的存储空间大小,存储到该组的元信息(头信息)中。这种编码方式就叫做Frame Of Reference (FOR) ,从Lucene 4.1开始沿用。
下图为Frames Of Reference的示例(将每3个文档id分成一组):
该图中的左边的block,最大的delta是227,最接近的2的整数次幂是256(8bits),于是规定这个block里的每一个数字都用8bits来编码;右边的block,最大的delta是30,最接近的2的整数次幂是32(5bits),于是规定这个block里都用5bits来编码。
在返回结果的时候,其实也并不需要把所有的数据直接解压然后全部返回,而是可以返回一个iterator ,然后通过iterator的next方法逐一取出被压缩的文档id,这样可以极大地节省算力和内存开销。
通过以上的方式可以极大的节省posting list的空间消耗,提高查询性能。不过ES为了提高filter过滤器查询的性能,还做了更多的工作,那就是缓存。
使用Roaring Bitmaps缓存常用filter查询的结果
在使用ES的时候,常常会使用filter查询。ES会缓存一些频率比较高的filter查询的结果。但是这个缓存与Posting List不同:
- 因为只需要缓存那些常用的filter查询的结果,因此压缩率并不是要考虑的首要条件;
- 因为需要这些filter查询的结果比真正执行filter查询要快,所以使用好的数据结构很重要;
- 缓存的常用的filter查询的结果是保存在内存中的,Posting List是保存在磁盘的;
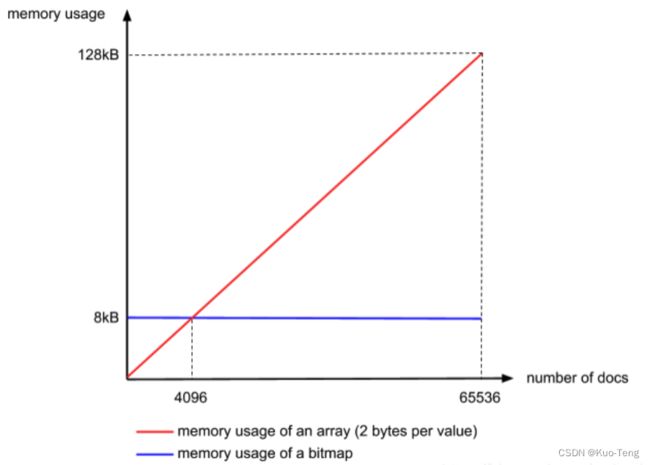
Roaring Bitmap 是由 Integer Array 和 Bitmap 这两个数据结构改良过的成果——Integer Array 速度快但是空间消耗大,Bitmap相对来说空间消耗小,但是存储空间随着文档个数线性增长。
Roaring Bitmap首先会根据每个id的高16位分配id到对应的block里面,比如第一个block里面id应该都是在0到65535之间,第二个block的id在65536和131071之间,以此类推。
对于每一个block里面的数据,如果文档id数量小于4096,就用 Integer Array 保存,文档id数量大于等于4096,就使用 Bitmap 保存。
为什么要设定一个4096的阈值呢?其实很简单,因为如果文档id数量小于4096,我们直接使用Integer Array,每个文档id需要2 bytes来存储(在每一个block里面,一个数字实际上只需要2 bytes 来保存就行了,因为高16位在这个block里面都是相同的),总的存储空间小于8192 bytes;而如果要使用Bitmap,因为每个block的大小是65536,因此所需Bitmap的大小是65536 bits 也就是8192 bytes;所以在文档id数量小于4096时直接使用 Integer Array 保存就可以了;
通过对Posting List取交集实现联合索引
在ES中,不需要特意添加联合索引,就可以快速检索同时满足多个条件的文档。
假如有三个查询关键词,我们会先得到每个关键词对应的Posting List,如下图所示:
然后对所有的Posting List取交集。
如果使用跳表,可以对最短的 Posting List 中的每个id,逐个在另外的Posting List中查找,判断其是否存在,最后得到交集的结果。
如果使用位图,可以直接进行按位与运算,得到的结果就是最后的交集。
然后根据交集中的文档id去找真正的文档就可以了。
总结
回到我们的文章标题,大规模数据量下ES是如何实现高性能检索的呢?
- ES通过分词然后对每一个单词及其对应文档建立倒排索引,使得能够快速根据关键词找到对应文档id;
- 建立了 Term Index,并通过FST压缩,将其缓存在内存中,能够高效地对映射关系中的 Term Dictionary 进行索引;
- 使用 Frames of Reference 对 Posting List 进行压缩,使其不至于太大,并且在返回结果的时候,返回一个iterator ,然后通过iterator的next方法逐一取出被压缩的文档id,提升查询性能;
- 使用 Roaring Bitmaps 将常用filter查询的结果直接缓存到内存中;
- 通过对多个查询条件对应的 Posting List 取交集实现联合索引;