【力扣——动态规划】整理题目3：打家劫舍、股票问题：198、213、337、121、122、123、188、309（附链接、题目描述、解题方法及代码）

如果对你有帮助的话
为博主点个赞吧
点赞是对博主最大的鼓励
爱心发射~

【动态规划整理合集】
【力扣——动态规划】整理题目1：基础题目：509、70、746、62、63、343、96
【力扣—动态规划】整理题目2：背包问题：0-1背包、完全背包

代码随想录知识星球

动态规划总结

解题步骤-简洁

1. 确定dp数组下标含义
2. 递推公式
3. 初始化
4. 遍历顺序
5. 推导结果

打家劫舍

198. 打家劫舍

likou

题解

动态规划

1. 确定dp数组下标含义 —— dp[i] = 偷到第i家时偷到的最多金额
2. 递推公式 —— dp[i] = max(dp[i-2]+nums[i], dp[i-1])
3. 初始化 —— dp[0] = nums[0] dp[1] = max(nums[0], nums[1])
4. 遍历顺序 —— 从前到后
5. 推导结果

class Solution {
    public int rob(int[] nums) {
        
        if(nums == null || nums.length == 0) return 0;
        if(nums.length == 1) return nums[0];

        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        dp[1] = Math.max(nums[0], nums[1]);
        for(int i=2; i<nums.length; i++){
            dp[i] = Math.max(dp[i-2]+nums[i], dp[i-1]);
        }
        return dp[nums.length-1];
    }
}

213. 打家劫舍 II

力扣

• 与1区别：成环
  
  

题解

class Solution {
    public int rob(int[] nums) {
        /*
        动态规划
        两种情况：
            - 包含首元素，不包含尾元素
            - 不包含首元素，包含尾元素
        其余 与1一样
        */
        if(nums == null && nums.length ==0) return 0;
        if(nums.length == 1) return nums[0];
        return Math.max(a(nums, 0, nums.length-1), a(nums, 1, nums.length));
    }

    int a(int[] nums, int start, int end){
        int x=0, y=0, z=0;
        for(int i=start; i<end; i++){
            y = z;
            z = Math.max(y, x + nums[i]);
            x = y;
        }
        return z;
    }
}

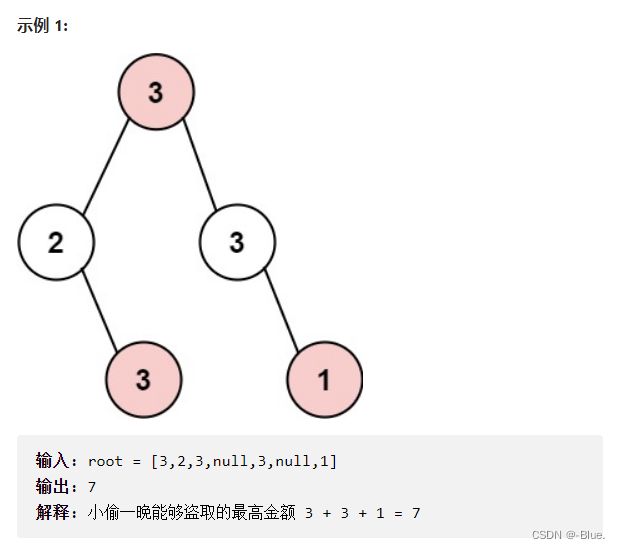
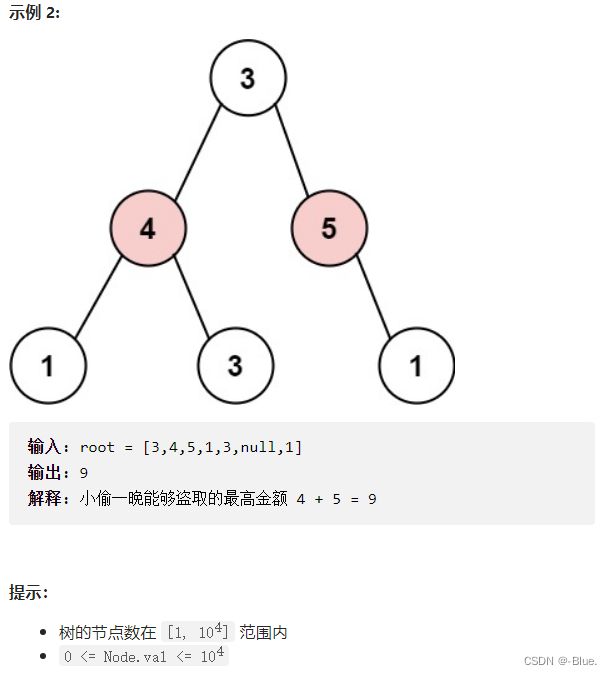
337. 打家劫舍 III

力扣

题解

0——不偷， 1——偷

• 不偷：Max(左孩子不偷，左孩子偷) + Max(又孩子不偷，右孩子偷)
  root[0] = Math.max(rob(root.left)[0], rob(root.left)[1]) + Math.max(rob(root.right)[0], rob(root.right)[1])

• 偷：左孩子不偷+ 右孩子不偷 + 当前节点偷
  root[1] = rob(root.left)[0] + rob(root.right)[0] + root.val;

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int rob(TreeNode root) {
        /*
        0——不偷， 1——偷
        不偷：Max(左孩子不偷，左孩子偷) + Max(又孩子不偷，右孩子偷)
            root[0] = Math.max(rob(root.left)[0], rob(root.left)[1]) +
                         Math.max(rob(root.right)[0], rob(root.right)[1])
        偷：左孩子不偷+ 右孩子不偷 + 当前节点偷
            root[1] = rob(root.left)[0] + rob(root.right)[0] + root.val;
        */
        int[] res = a(root);
        return Math.max(res[0], res[1]);
    }
    int[] a(TreeNode root){
        int[] res = new int[2];
        if(root == null) return res;
        int[] left = a(root.left);
        int[] right = a(root.right);
        res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        res[1] = root.val + left[0] + right[0];
        return res;
    }
}

股票问题

121. 买卖股票的最佳时机

力扣

1、 确定dp数组下标含义

• dp[i][0] 表示第i天持有股票所得最多现金
• dp[i][1] 表示第i天不持有股票所得最多现金

2、递推公式

dp[i][0] 第i天持有股票时所得的现金 dp[i][0]= max(dp[i-1][0], -prices[i])

• i-1天就持有股票 dp[i-1][0]
• i天 买的股票 -prices[i]

dp[i][1] 第i天不持有股票所得最多现金 dp[i][1]=max(dp[i-1][1], dp[i-1][0] + prices[i])

• i-1 就已经卖出 dp[i-1][1]
  -i天卖出 prices[i]

3、初始化

• dp[0][0] = -prices[0]
• dp[0][1] = 0

4、 遍历顺序

• 从前到后

5、 推导结果

题解

class Solution {
    public int maxProfit(int[] prices) {
        /*
            1. 确定dp数组下标含义   
                dp[i][0] 表示第i天持有股票所得最多现金 
                dp[i][1] 表示第i天不持有股票所得最多现金 
            2. 递推公式 
                dp[i][0] 第i天持有股票时所得的现金 dp[i][0]= max(dp[i-1][0], -prices[i])
                    - i-1天就持有股票  dp[i-1][0]
                    - i天 买的股票     -prices[i]
                dp[i][1] 第i天不持有股票所得最多现金 dp[i][1]=max(dp[i-1][1], dp[i-1][0] +  prices[i])
                    - i-1 就已经卖出   dp[i-1][1]
                    - 天卖出           prices[i]
            3. 初始化 
                dp[0][0] = -prices[0] 
                dp[0][1] = 0
            4. 遍历顺序   从前到后
            5. 推导结果
        */
		
		// 方法一
        if(prices == null || prices.length ==0) return 0;
        int res = 0;
        int[][] dp = new int[prices.length][2];
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        for(int i=1; i<prices.length; i++){
            dp[i][0] = Math.max(dp[i-1][0], -prices[i]);
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] + prices[i]);
        }
        return dp[prices.length-1][1];
		
		// 方法二 0 持有   1 不持有
        if(prices == null || prices.length ==0) return 0;
        int res = 0;
        int[] dp = new int[2];
        dp[0] = -prices[0];
        dp[1] = 0;
        for(int i=1; i<prices.length; i++){
            dp[0] = Math.max(dp[0], -prices[i]);
            dp[1] = Math.max(dp[0]+prices[i], dp[1]);
        }
        return dp[1];
    }
}

122. 买卖股票的最佳时机 II

力扣

题解

class Solution {
    public int maxProfit(int[] prices) {
        /*
        1. 确定dp数组下标含义 
            dp[i][0] 表示第i天持有股票所得最大利润
                    = 前一天买的股票 + 前一天没有股票，今天买的股票
            dp[i][1] 表示第i天不持有股票所得最大利润
                    = 前一天没有股票 + 前一天有股票，今天卖的
        2. 递推公式 
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i])
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])
        3. 初始化 
            dp[0][0] = prices[0]
            dp[0][1] = 0
        4. 遍历顺序 ：从前到后
        5. 推导结果
        */
        if(prices == null || prices.length ==0) return 0;
        int[][] dp = new int[prices.length][2];
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        for(int i=1; i<prices.length; i++){
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] - prices[i]);
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] + prices[i]);
        }
        return dp[prices.length-1][1];

        // 优化空间——一维数组
        if(prices == null || prices.length ==0) return 0;
        int[] dp = new int[2];
        dp[0] = -prices[0];
        dp[1] = 0;
        for(int i=1; i<prices.length; i++){
            dp[0] = Math.max(dp[0], dp[1] - prices[i]);
            dp[1] = Math.max(dp[1], dp[0] + prices[i]);
        }
        return dp[1];

    }
}

123. 买卖股票的最佳时机 III

likou

题解

class Solution {
    public int maxProfit(int[] prices) {
        /*
            0 —— 第一次买股票
            1 —— 第一次卖
            2 —— 第二次买
            3 —— 第二次卖
        */
        int[] dp = new int[4];
        dp[0] = -prices[0];
        dp[1] = 0;
        dp[2] = -prices[0];
        dp[3] = 0;
        for(int i=1; i<prices.length; i++){
            dp[0] = Math.max(dp[0], -prices[i]);
            dp[1] = Math.max(dp[1], dp[0] + prices[i]);
            dp[2] = Math.max(dp[2], dp[1] - prices[i]);
            dp[3] = Math.max(dp[3], dp[2] + prices[i]);
        }
        return dp[3];
    }
}

188. 买卖股票的最佳时机 IV

力扣

题解

class Solution {
    public int maxProfit(int k, int[] prices) {
        /*
        二维数组：
            0 —— 无操作
            1 —— 持有股票   奇数
            2 —— 卖出股票   偶数
        */
        if(prices.length == 0) return 0;
        int[][] dp = new int[prices.length][2*k + 1];
        for(int i=1; i<2*k; i+=2){
            dp[0][i] = -prices[0];
        }
        for(int i=1; i<prices.length; i++){
            for(int j=0; j<2*k - 1; j+=2){
                dp[i][j+1] = Math.max(dp[i-1][j+1], dp[i-1][j] - prices[i]);
                dp[i][j+2] = Math.max(dp[i-1][j+2], dp[i-1][j+1] + prices[i]);
            }
        }
        return dp[prices.length-1][2*k];
    }
}

309. 最佳买卖股票时机含冷冻期

likou

题解

class Solution {
    public int maxProfit(int[] prices) {
        /*
            0 持有股票
                前一天就有，前一天没有今天买的，前一天冷冻期今天买
            1 今天卖出股票
                前一天有今天卖
            2 卖出股票状态
                前一天就是这个状态，前一天是冷冻期
            3 冷冻期
                前一天卖的
        */
        if(prices == null || prices.length < 2) return 0;
        int[] dp = new int[4];
        dp[0] = -prices[0];
        dp[2] = 0;
        for(int i=1; i<prices.length; i++){
            int b1 = dp[0];
            int b2 = dp[1];
            dp[0] = Math.max(dp[0], Math.max(dp[2] - prices[i], dp[3]-prices[i]));
            dp[1] = b1 + prices[i];
            dp[2] = Math.max(dp[2], dp[3]);
            dp[3] = b2;
        }
        return Math.max(dp[3], Math.max(dp[1], dp[2]));
    }
}