电商数据分析--薪资预测(线性回归)
电商数据分析–薪资预测(线性回归)
数据分析流程:
- 明确目的
- 获取数据
- 数据探索和预处理
- 分析数据
- 得出结论
- 验证结论
- 结果展现
线性回归:线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。其表达形式为y = w’x+e,e为误差服从均值为0的正态分布。 回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。(常用于需求预测、销量预测、排名预测)
一元线性回归方程: y = b + a X y=b+aX y=b+aX
b为截距,a为回归直线的斜率
多元线性回归方程: y = b 0 + b 1 X 1 + b 2 X 2 + . . . + b n X n y=b0+b1X1+b2X2+...+bnXn y=b0+b1X1+b2X2+...+bnXn
b 0 为 常 数 项 , b 1 , b 2 , b 3 , b n 为 y 对 应 与 X 1 , X 2 , X 3.. X n 的 偏 回 归 系 数 。 b0为常数项,b1,b2,b3,bn为y对应与X1,X2,X3..Xn的偏回归系数。 b0为常数项,b1,b2,b3,bn为y对应与X1,X2,X3..Xn的偏回归系数。
skearn库-线性回归(LinearRegression)
具体参数解释以及调用方式:
from sklearn.linear_model import LinearRegression
LinearRegression(fit_intercept=True,normalize=False.copy_x=True,n_jobs=1)
参数含义:
1、fit_intercept:布尔值,指定是否需要计算线性回归中的截距,即b值。如果为False,那么不计算b值。
2、normalize:布尔值。如果为False,那么训练样本会进行归一化处理。
3、copy_x:布尔值。如果为True,会复制一份训练数据,
4、n_jobs:一个整数。任务并行时指定的CPU数量。如果取值为-1则使用所有可用的CPU。
属性:
1、coef_:权重向量
2、intercept_:截距b值
方法:
1、fit(X,y):训练模型
2、predict(X):用训练号的模型进行预测,并返回预测值。
3、score(X,y):返回预测性能的得分。计算公式为:score=(1-u/v)
其中u=((y_ture-y_pred)**2).sum(),v=((y_true-y_ture.mean())**2).sum()
score最大值是1,但有可能是负值(预测效果太差)。score越大,预测性能越好。
薪资预测案例实现
#调用数据分析必要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model #线性模型
#导入数据
single_variable = pd.read_csv(r"E:\数据分析\ingle_variable.csv")
print(single_variable) #查看数据
print(single_variable.shape)
print(single_variable.isnull().any()) #是否存在缺失值
#准备数据
length = len(single_variable['work_length'])
X = np.array(single_variable['work_length']).reshape([length,1])
Y = np.array(single_variable['year_salary'])
#绘图观察数据
#绘制散点图,X,Y,设置颜色,标记点样式和透明度等参数
plt.scatter(X,Y,60,color='blue',marker='o',linewidth=3,alpha=0.8)
#添加x轴标题
plt.xlabel('work years')
#添加y轴标题
plt.ylabel('year salary')
#添加图表标题
plt.title('work years and year salary')
#设置背景网格线颜色,样式,尺寸和透明度
plt.grid(color='#95a5a6',linestyle='--', linewidth=1,axis='both',alpha=0.4)
#显示图表
plt.show()
#调用线性回归模型
linear=linear_model.LinearRegression()
linear.fit(X,Y)
#查看截距和系数
print(linear.coef_ )
print(linear.intercept_)
#查看拟合效果得分
print(linear.score(X,Y))
#新数据预测
x_new = np.array(8).reshape(1, -1)
y_pred =linear.predict(x_new)
print(y_pred)
#最终得出 y = ax+b
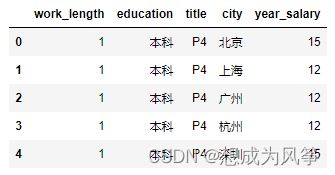
多元线性回归(工作年限、地点、教育水平、等级与薪资),数据如图所示。
#调用数据分析必要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model #线性模型
#导入数据
many_variable = pd.read_csv(r"E:\数据分析\many_variable.csv")
print(many_variable) #查看数据
print(many_variable.shape)
print(many_variable.isnull().any()) #是否存在缺失值
#数据处理
many_variable['education']=many_variable['education'].replace(['本科','研究生'],
[1,2])
many_variable['city']=many_variable['city'].replace(['北京','上海','广州','杭州','深圳'],
[1,2,3,4,5])
many_variable['title']=many_variable['title'].replace(['P4','P5','P6','P7'],
[1,2,3,4])
#查看数据
print(many_variable)
#准备数据
x = np.array(many_variable[['work_length','education','title','city']])
y = np.array(many_variable['year_salary'])
#切分数据集(训练集和测试集)
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(x,y,test_size=0.4,random_state=1)
#调用线性回归模型
linear2 = linear_model.LinearRegression()
linear2.fit(X_train,y_train)
#查看截距和系数
print(linear2.coef_ )
print(linear2.intercept_)
#查看拟合效果得分
print(linear2.score(X,Y))
#新数据预测
y_pred =list(linear2.predict(X_test))
print(y_pred)
#最终得出 y=1.35+1.1*work_length+5.19*education+5.92*title+0.09*city
