一文解决剑指Offer所有搜索回溯问题
文章目录
-
-
- 1. 剑指 Offer 32 - I. 从上到下打印二叉树
- 2. 剑指 Offer 32 - II. 从上到下打印二叉树 II
- 3. 剑指 Offer 32 - III. 从上到下打印二叉树 III
- 4. 剑指 Offer 26. 树的子结构
- 5. 剑指 Offer 27. 二叉树的镜像
- 6. 剑指 Offer 28. 对称的二叉树
- 7. 剑指 Offer 12. 矩阵中的路径
- 8. 剑指 Offer 13. 机器人的运动范围
- 9. 剑指 Offer 34. 二叉树中和为某一值的路径
- 10. 剑指 Offer 36. 二叉搜索树与双向链表
- 11. 剑指 Offer 54. 二叉搜索树的第k大节点
- 12. 剑指 Offer 64. 求1+2+…+n
- 13. 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
- 14. 剑指 Offer 68 - II. 二叉树的最近公共祖先
- 15. 剑指 Offer 37. 序列化二叉树
- 16. 剑指 Offer 38. 字符串的排列
- 17. 剑指 Offer 55 - I. 二叉树的深度
- 18. 剑指 Offer 55 - II. 平衡二叉树
-
1. 剑指 Offer 32 - I. 从上到下打印二叉树
剑指 Offer 32 - I. 从上到下打印二叉树
思路:使用队列进行层次遍历即可
class Solution {
public int[] levelOrder(TreeNode root) {
if(root==null)
return new int[0];//root为null时,返回[]
ArrayList<Integer> list=new ArrayList<>();
LinkedList<TreeNode> q=new LinkedList<>();
q.offer(root);
while(!q.isEmpty())
{
TreeNode node=q.pop();
list.add(node.val);
if(node.left!=null)
q.add(node.left);
if(node.right!=null)
q.add(node.right);
}
int ans[]=new int[list.size()];
for(int i=0;i<list.size();i++)
{
ans[i]=list.get(i);
}
return ans;
}
}
//O(n) BFS需要循环N次
//O(n/2) 当数是平衡二叉树时,最多有n/2个节点在队列中
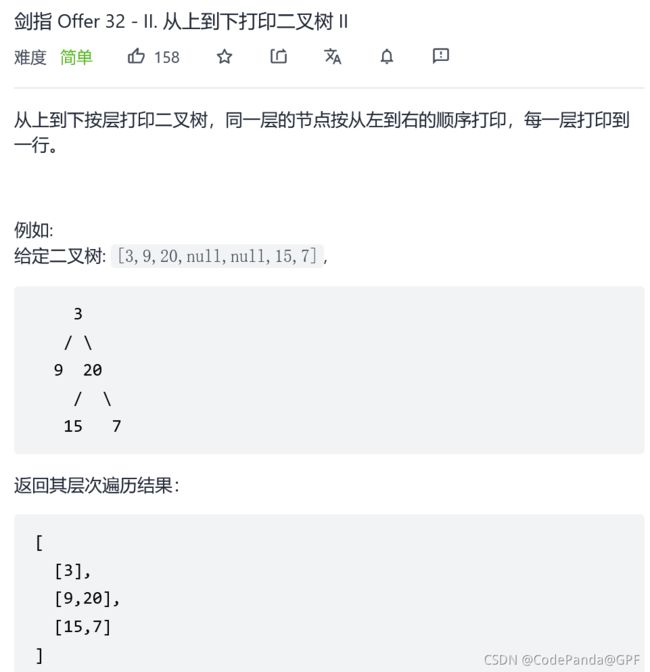
2. 剑指 Offer 32 - II. 从上到下打印二叉树 II
剑指 Offer 32 - II. 从上到下打印二叉树 II
思路:使用队列进行层次遍历,但是需要将每一层的节点作为一个list记录下来, 即在内部还需要对每一层进行单独遍历
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> list=new ArrayList<>();
if(root==null)
return list;
LinkedList<TreeNode> q=new LinkedList<>();
q.offer(root);
while(!q.isEmpty())
{
int size=q.size();
List<Integer> level=new ArrayList<>();
for(int i=0;i<size;i++)//遍历每一层
{
TreeNode node=q.pop();
level.add(node.val);
if(node.left!=null)
q.offer(node.left);
if(node.right!=null)
q.offer(node.right);
}
list.add(level);
}
return list;
}
}
//O(n) BFS需要循环N次
//O(n/2) 当数是平衡二叉树时,最多有n/2个节点在队列中
3. 剑指 Offer 32 - III. 从上到下打印二叉树 III
剑指 Offer 32 - III. 从上到下打印二叉树 III

思路:使用队列进行层次遍历,对于每一层进行添加的顺序不一样,第1层从左到右添加,第2列从右到左添加…可以设置一个层号,奇数层正序添加,偶数列逆序添加
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> list=new ArrayList<>();
if(root==null)
return list;
LinkedList<TreeNode> q=new LinkedList<>();
q.offer(root);
int levelNum=1;//层号初始化为1
while(!q.isEmpty())
{
int size=q.size();
//这里使用LinkedList便于倒着添加节点
LinkedList<Integer> level=new LinkedList<>();
for(int i=0;i<size;i++)//遍历每一层
{
TreeNode node=q.pop();
if(levelNum%2!=0)//奇数层 顺着添加
level.addLast(node.val);
else//偶数层 倒着添加
level.addFirst(node.val);
if(node.left!=null)
q.offer(node.left);
if(node.right!=null)
q.offer(node.right);
}
list.add(level);
levelNum++;
}
return list;
}
}
4. 剑指 Offer 26. 树的子结构
剑指 Offer 26. 树的子结构
思路:遍历树A的每一个节点a,然后以判断以a为根节点的是否存在一个子树和B一样,一样则返回true,否则继续判断,分布以a的左子节点和右子节点开始比较,如果树A遍历完了还没有返回true,则说明B不是A的子树;在比较的过程中,如果树B遍历完了还没有返回false则说明B是A的一个子树,需要两个函数,一个isSubstructue()用来深度遍历,一个judge用来判断当前节点开始的子树是否和B一样
class Solution {
public boolean isSubStructure(TreeNode A, TreeNode B) {
//只要有一个树为null,就返回false
if(A==null||B==null)
return false;
//下面不是三个judge,因为需要要的是一个先序遍历(dfs),如果
//当前节点开始不存在子结构,则下一次以当前节点的左子节点开始
//再次比较,然后再左子节点
return judge(A,B)||isSubStructure(A.left,B)||isSubStructure(A.right,B);
}
boolean judge(TreeNode A,TreeNode B)
{
if(B==null)//B树遍历完了还没有返回false 说明是true 先判断B树是否遍历完
return true;
if(A==null)//A树遍历完了,B树还没有遍历完
return false;
if(A.val!=B.val)//当前节点不相等
return false;
//当前节点相等 接着比较左子节点和右子节点的值
return judge(A.left,B.left)&&judge(A.right,B.right);
}
}
//O(MN) M是A的节点数目 N是B的节点数目 遍历A需要O(M) 对于A的每个节点需要调用recur使用O(N)
//O(M)
5. 剑指 Offer 27. 二叉树的镜像
剑指 Offer 27. 二叉树的镜像
思路1:使用递归深度搜索,从下到上进行节点的交换
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if(root==null)
return null;
TreeNode tmp=root.left;
root.left=mirrorTree(root.right);
root.right=mirrorTree(tmp);
return root;
}
}
//O(N)
//O(N)
思路2:使用辅助队列层次遍历,从上到下进行节点的交换
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if(root==null)
return null;
LinkedList<TreeNode> q=new LinkedList<>();
q.offer(root);
while(!q.isEmpty())
{
TreeNode node=q.pop();
if(node.left!=null)
q.offer(node.left);
if(node.right!=null)
q.offer(node.right);
TreeNode tmp=node.left;
node.left=node.right;
node.right=tmp;
}
return root;
}
}
//O(N)
//O(N)
6. 剑指 Offer 28. 对称的二叉树
剑指 Offer 28. 对称的二叉树
思路:采用递归,分别判断当前节点左节点L和右节点R,如果是一个对称二叉树,则有L.val==R.val L.left.val==R.right.val L.right.val==R.left.val,比较函数judge递归中
终止条件为:
- L R同时为null 即同时越过叶子节点 此时返回true
- L R没有同时越过叶子节点,返回false
- 二者不为null,但是当前的值不相同 返回false
- 不满足1-3的递归终止条件的话则继续比较 (A左比较B右 A右比较B左)
时间复杂度:O(n) n是节点的数目 每次判断一对节点 最多判断n/2次
空间复杂度:O(n)
class Solution {
public boolean isSymmetric(TreeNode root) {
//树为空直接返回true
if(root==null)
return true;
return judge(root.left,root.right);
}
boolean judge(TreeNode leftTree,TreeNode rightTree)
{
//左右子树同时达到叶子节点,说明对称
if(leftTree==null&&rightTree==null)
return true;
//左右子树没有同时到达叶子节点,说明不对称
if(leftTree==null||rightTree==null)
return false;
//只要遇到一个节点的值不相同就返回false
if(leftTree.val!=rightTree.val)
return false;
//当前节点相同但是左右子树没有遍历完 继续遍历
return judge(leftTree.left,rightTree.right) &&judge(leftTree.right,rightTree.left);
}
}
7. 剑指 Offer 12. 矩阵中的路径
剑指 Offer 12. 矩阵中的路径
思路:深度搜索,搜索的开始位置有m*n个,注意搜索函数dfs中的终止条件,注意点:一个网格在一次搜索中不能被多次访问,因此需要将其设置为’\0’来表示已经访问,搜索结束之后再将\0还原成原来的字符(当然也可以另外使用一个标记访问数组,但是会增加空间开销)
时间复杂度 O(3 K ^K KMN) : 最差情况下,需要遍历矩阵中长度为 K字符串的所有方案,时间复杂度为 O(3 K ^K K);矩阵中共有 MN个起点,时间复杂度为 O(MN) 。
方案数计算: 设字符串长度为 K ,搜索中每个字符有上、下、左、右四个方向可以选择,舍弃回头(上个字符)的方向,剩下 333 种选择,因此方案数的复杂度为 O(3^K)空间复杂度 O(K) : 搜索过程中的递归深度不超过 K ,因此系统因函数调用累计使用的栈空间占用 O(K) (因为函数返回后,系统调用的栈空间会释放)。最坏情况下 K=MN ,递归深度为 MN ,此时系统栈使用 O(MN) 的额外空间
class Solution {
public boolean exist(char[][] board, String word) {
int m=board.length;
int n=board[0].length;
int index=0;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
if(dfs(board,word,i,j,index))//m*n个出发位置
return true;
}
return false;
}
public boolean dfs(char [][] board,String word,int i,int j,int index)
{
if(i<0||i>=board.length||j>=board[0].length||j<0||board[i][j]!=word.charAt(index))//停止寻找的条件
return false;
if(index==word.length()-1)//匹配成功
return true;
board[i][j]='\0';//将(i,j)位置标记为已经访问过
boolean ans= dfs(board,word,i+1,j,index+1)||dfs(board,word,i,j+1,index+1)|| dfs(board,word,i-1,j,index+1)|| dfs(board,word,i,j-1,index+1);//向上下左右四个位置继续搜索,一个为true即可 不要单独写,这样就不能发挥短路或的作用
board[i][j]=word.charAt(index);//还原标记
return ans;
}
}
8. 剑指 Offer 13. 机器人的运动范围
剑指 Offer 13. 机器人的运动范围
思路:深度搜索,和上一题类似,但是有一点不同,本题的出发点只有一个,由于只有一次搜索且访问过之后就不需要再次访问了,故不用还原
class Solution {
int count=0;
public int movingCount(int m, int n, int k) {
//标记数组 判断(i,j)位置是否被访问过
boolean visited[][]=new boolean[m][n];
dfs(0,0,m,n,k,visited);//开始位置只有一个(0,0)
return count;
}
public void dfs(int i,int j,int m,int n,int k,boolean[][] visited)
{
if(i<0||i>=m||j<0||j>=n||visited[i][j]==true||calNum(i,j)>k)
return;//终止条件
count++;
visited[i][j]=true;//(i,j)位置已经访问过
dfs(i+1,j,m,n,k,visited);//向下走
dfs(i-1,j,m,n,k,visited);//向上走
dfs(i,j+1,m,n,k,visited);//向右走
dfs(i,j-1,m,n,k,visited);//向走走
//visited[i][j]不用还原 因为只有一次搜索 出发位置只有一个
}
public int calNum(int i,int j)
{
//i,j都是1位数或者两位数
int ans=i/10+i%10+j/10+j%10;//计算数位之和
return ans;
}
}
//O(mn)
//O(mn)
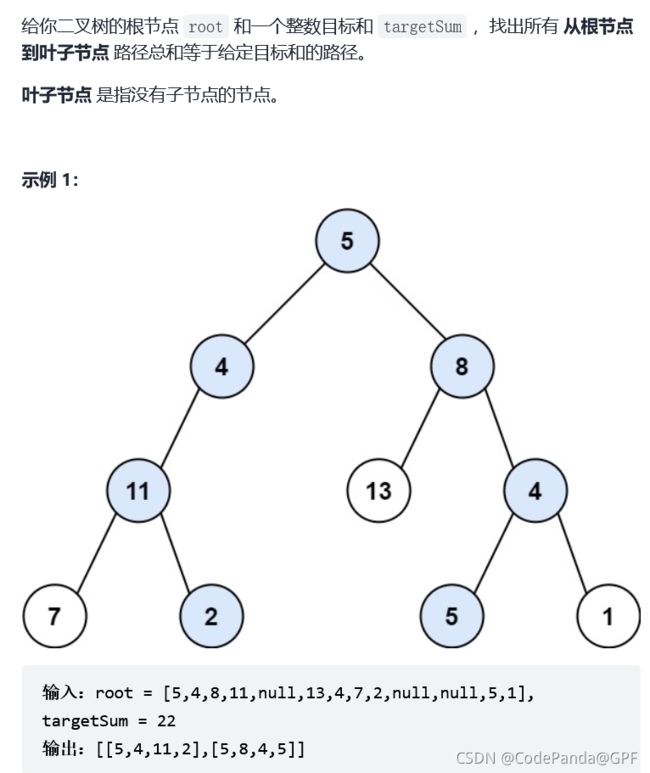
9. 剑指 Offer 34. 二叉树中和为某一值的路径
剑指 Offer 34. 二叉树中和为某一值的路径
思路:深度优先搜索,对于树而言也是先序遍历,遍历时判断是否时叶子节点且路径和是否等于target
class Solution {
List<List<Integer>> ans=new ArrayList<>();
public List<List<Integer>> pathSum(TreeNode root, int target) {
List<Integer> list=new ArrayList<>();
dfs(root,target,list);
return ans;
}
public void dfs(TreeNode root,int target, List<Integer> list)
{
if(root==null)
return;
list.add(root.val); //添加当前节点
//符合节点值和=target并且是叶子节点
if(target==root.val&&root.left==null&&root.right==null)
{
ans.add(new ArrayList<>(list));//必须用new创建一个新的
}
dfs(root.left,target-root.val,list);//遍历左子树
dfs(root.right,target-root.val,list);//遍历右子树
list.remove(list.size()-1);//该路径的和不等于target
//路径恢复:向上回溯前需要删除刚刚添加的元素
}
}
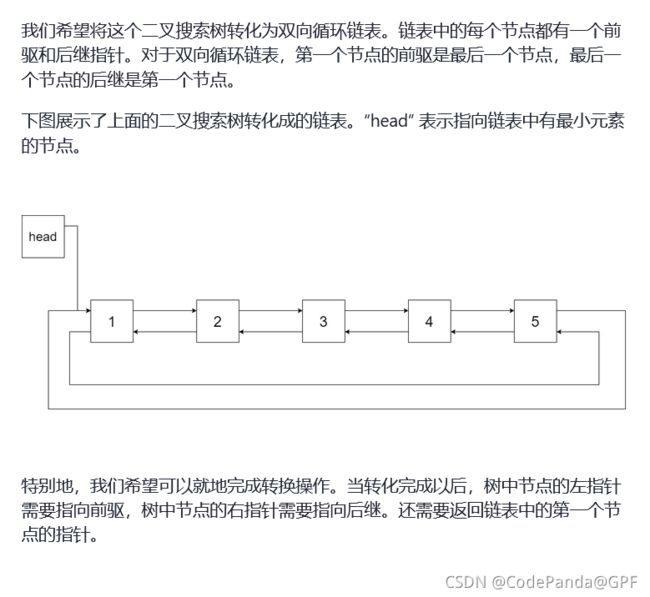
10. 剑指 Offer 36. 二叉搜索树与双向链表
思路:
- 要求升序 而且是二叉搜索树,因此可以采用中序遍历
- 在构建相邻节点的引用关系时,设前驱节点
pre和当前节点cur,不仅应构建pre.right = cur,也应构建cur.left = pre- 设链表头节点
head和尾节点tail,则应构建head.left = tail和tail.right = head
class Solution {
Node head,pre;//默认值为null
public Node treeToDoublyList(Node root) {
if(root==null)//root为空则直接返回 否则head为null head.left会出现空指针异常
return null;
dfs(root);
//题目要求头尾连接 head最终指向头 pre指向尾
head.left=pre;//head的左指针指向pre尾结点
pre.right=head;//pre的右指针指向head头节点
return head;//返回头指针
}
public void dfs(Node cur)
{
if(cur==null)
return;//递归结束条件
dfs(cur.left);//中序遍历: 左根右
if(pre==null)//pre为空 说明cur指向第一个节点
head=cur;//因此head指向头节点
else//pre不为空 说明cur指向的是非头结点 pre指向上一个节点
pre.right=cur;//上一个节点的右指针指向当前节点
cur.left=pre;//当前节点的左指针指向上一个节点
pre=cur;//保存当前节点 用于下层递归创建
dfs(cur.right);
}
}
//O(n) n为二叉树的节点数目
//O(n)
11. 剑指 Offer 54. 二叉搜索树的第k大节点
剑指 Offer 54. 二叉搜索树的第k大节点
思路:由于是二叉搜索树,中序遍历之后是升序的,最后一个元素是最大的,题目要求第k大的,也就是中序遍历之后的倒数第K个元素,为了方便起见,可以根据
右根左的遍历顺序得到一个中序遍历的逆序序列,这样就是正数第K个元素,在遍历过程中不断地使K–,K==0说明找到了第K大的节点
class Solution {
int ans,k;//k应该设置为成员变量
public int kthLargest(TreeNode root, int k) {
this.k=k;
inOrderReverse(root);
return ans;
}
public void inOrderReverse(TreeNode root)
{
if(root==null)
return;
//中序升序:左根右 中序逆序:右根左
inOrderReverse(root.right);//右根左
k--;//计数减一
if(k==0)//遍历到第k大的节点,即逆序的第k个节点
{
ans=root.val;
return;
}
inOrderReverse(root.left);
}
}
//O(n) 最坏情况下 二叉树退化为只有右子节点的链表
//O(n)
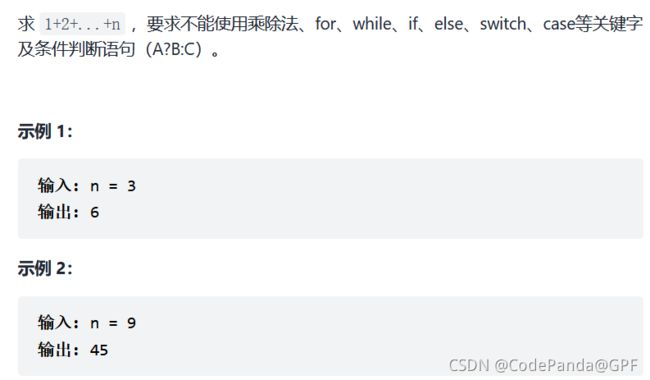
12. 剑指 Offer 64. 求1+2+…+n
剑指 Offer 64. 求1+2+…+n
思路:利用&&的短路性来实现if判断的功能
class Solution {
int sum;
public int sumNums(int n) {
//x没有啥意义 只是为了构成一个布尔表达式
//n如果=0的话 后面的sumNums(n-1)就不会进去 相当于1个if判断
boolean x=(n>0)&&(sumNums(n-1)>0);
sum+=n;
return sum;
}
}
//O(n)
//O(n)
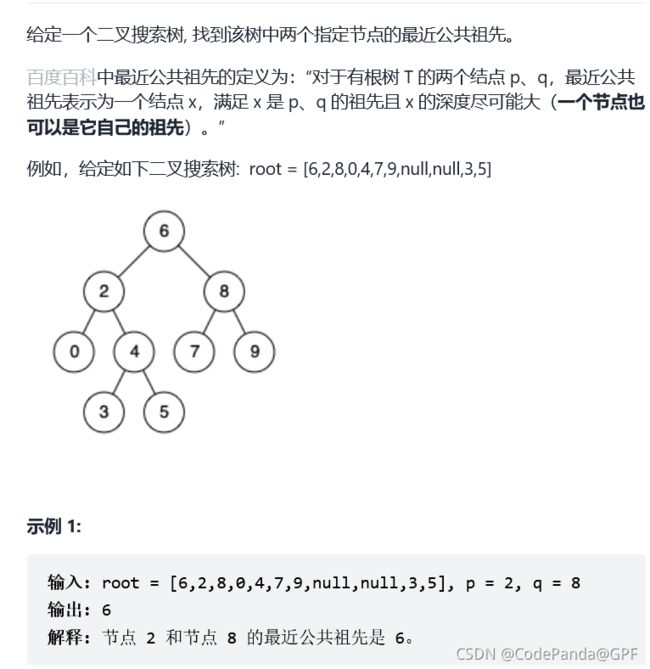
13. 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
思路:利用二叉搜索树的性质,左子节点<根节点<右子节点具体的解决方法可以采用迭代或者递归
//迭代
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
while(root!=null)
{
if(root.val>p.val&&root.val>q.val)//p q位于当前root节点的左子树中
root=root.left;
else if(root.val<p.val&&root.val<q.val)//p q位于当前root节点的右子树中
root=root.right;
else//p q节点位于root节点的左右子树中 说明root是最近公共节点
break;
}
}
}
//递归
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root.val>p.val&&root.val>q.val)
return lowestCommonAncestor(root.left,p,q);
else if(root.val<p.val&&root.val<q.val)
return lowestCommonAncestor(root.right,p,q);
return root;
}
}
14. 剑指 Offer 68 - II. 二叉树的最近公共祖先
剑指 Offer 68 - II. 二叉树的最近公共祖先
思路: 若root是p,q节点的最近公共祖先,则只可能是下列3种情况之一:
- p,q位于root的左右子树中
- root=p,q位于root的左子树或右子树中
- root=q,p位于root的左子树或右子树中
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null)// 如果树为空,直接返回null
return null;
if(root==p||root==q)// 如果 p和q中有等于 root的,那么它们的最近公共祖先即为root(一个节点也可以是它自己的祖先)
return root;
// 递归遍历左子树,只要在左子树中找到了p或q,则先找到谁就返回谁
TreeNode left=lowestCommonAncestor(root.left,p,q);
// 递归遍历右子树,只要在右子树中找到了p或q,则先找到谁就返回谁
TreeNode right=lowestCommonAncestor(root.right,p,q);
if(left==null&&right==null)
return null;
// 如果在左子树中 p和 q都找不到,则 p和 q一定都在右子树中,右子树中先遍历到的那个就是最近公共祖先(一个节点也可以是它自己的祖先)
if(left==null)
return right;
// 如果在右子树中 p和 q都找不到,则 p和 q一定都在左子树中,左子树中先遍历到的那个就是最近公共祖先(一个节点也可以是它自己的祖先)
if(right==null)//left!=null&&right!=null 说明root就是最近公共节点
return left;
return root;
}
}
//O(n)
//O(n)
15. 剑指 Offer 37. 序列化二叉树
思路:使用BFS或DFS 注意的一点是需要将二叉树的空节点也补上,使得二叉树表示完整
DFS序列化后的序列:1,2,#,#,3,4,#,#,5,#,#,
BFS序列化后的序列:1,2,3,#,#,4,5,#,#,#,#,
//DFS
public class Codec {
String SEP=",";//分隔符表示
String NULL="#";//空指针表示
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
StringBuilder sb=new StringBuilder();
serialize(root,sb);
return sb.toString();
}
public void serialize(TreeNode root,StringBuilder sb)
{ if(root==null)
{
sb.append(NULL).append(SEP);
return;
}
//前序遍历
sb.append(root.val).append(SEP);
serialize(root.left,sb);
serialize(root.right,sb);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
String str[]=data.split(SEP);
LinkedList<String> nodes=new LinkedList<>();
for(String s:str)
{
nodes.addLast(s);
}
return deserialize(nodes);
}
public TreeNode deserialize(LinkedList<String> nodes)
{
String firstNode=nodes.removeFirst();//前序序列的第一个节点
if(firstNode.equals(NULL))//当前nodes中的元素是null
return null;
TreeNode root=new TreeNode(Integer.parseInt(firstNode));
root.left=deserialize(nodes);
root.right=deserialize(nodes);
return root;
}
}
//O(n)
//O(n)
class Codec {
public:
char SEP=',';
string null_ptr="#";
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
string str;
serialize(root,str);
return str;
}
void serialize(TreeNode* root,string &str) {
if(root==NULL)
{
str+=(null_ptr+SEP);
return;
}
str+=to_string(root->val)+SEP;//c++中整数不能和字符串直接相加 先将整数转化为字符串
serialize(root->left,str);
serialize(root->right,str);
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
list<string> nodes;
string s;
for(int i=0;i<data.size();i++)
{
if(data[i]==SEP)
{
nodes.push_back(s);
s.clear();
}
else
{
s+=data[i];
}
}
return deserialize(nodes);
}
TreeNode* deserialize(list<string> &nodes)
{
string s=nodes.front();
nodes.pop_front();
if(s==null_ptr)
return NULL;//c++中的空指针是NULL Java中的null
TreeNode *node=new TreeNode(stoi(s));//stoi 在头文件中
node->left=deserialize(nodes);
node->right=deserialize(nodes);
return node;
}
};
//BFS
public class Codec {
String SEP=",";//分隔符表示
String NULL="#";//空指针表示
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if(root==null)
return "";
StringBuilder sb=new StringBuilder();
Queue<TreeNode> q=new LinkedList<>();
q.offer(root);
while(!q.isEmpty())
{
TreeNode node=q.poll();
if(node!=null)
{
sb.append(node.val).append(SEP);
q.offer(node.left);
q.offer(node.right);
}
else
sb.append(NULL).append(SEP);
}
// sb.deleteCharAt(sb.length());//删除最后一个逗号
return sb.toString();
}
public TreeNode deserialize(String data)
{
if(data.equals(""))
return null;//空树
//substring(1,data.length()-1) 去掉首尾的[]
String val[]=data.split(SEP);
Queue<TreeNode> q=new LinkedList<>();
TreeNode root=new TreeNode(Integer.parseInt(val[0]));
q.offer(root);
int i=1;
while(!q.isEmpty())
{
TreeNode node=q.poll();
if(!val[i].equals(NULL))
{
node.left=new TreeNode(Integer.parseInt(val[i]));
q.offer(node.left);
}
i++;
if(!val[i].equals(NULL))
{
node.right=new TreeNode(Integer.parseInt(val[i]));
q.offer(node.right);
}
i++;
}
return root;
}
}
//O(n)
//O(n)
16. 剑指 Offer 38. 字符串的排列
剑指 Offer 38. 字符串的排列
思路:交换,回溯
class Solution {
ArrayList<String> lists=new ArrayList<>();
char c[];
public String[] permutation(String s) {
c=s.toCharArray();
backtrack(0);
return lists.toArray(new String[lists.size()]);
}
public void backtrack(int x)
{
if(x==c.length-1)
{
lists.add(String.valueOf(c));
return;
}
ArrayList<Character> list=new ArrayList<>();
for(int i=x;i<c.length;i++)
{
if(list.contains(c[i]))//判断是否包含将要加入的元素
continue;
//如果s="aab" 我们只需要固定第一个a 遇到第2个a直接跳过
list.add(c[i]);
swap(i,x);
backtrack(x+1);
swap(x,i);
}
}
//交换实现全排列
public void swap(int x,int i)
{
char tmp=c[i];
c[i]=c[x];
c[x]=tmp;
}
}
17. 剑指 Offer 55 - I. 二叉树的深度
思路1:DFS
时间复杂度:O(n)
空间复杂度:O(n)
class Solution {
public int maxDepth(TreeNode root) {
if(root==null)
return 0;
return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
}
}
思路2: BFS
时间复杂度:O(n)
空间复杂度:O(n)
class Solution {
public int maxDepth(TreeNode root) {
if(root==null)
return 0;
int depth=0;
LinkedList<TreeNode> q=new LinkedList<>();
q.offer(root);
while(!q.isEmpty())
{
int sz=q.size();
for(int i=0;i<sz;i++)
{
TreeNode node=q.poll();
if(node.left!=null)
q.offer(node.left);
if(node.right!=null)
q.offer(node.right);
}
depth++;
}
return depth;
}
}
18. 剑指 Offer 55 - II. 平衡二叉树
剑指 Offer 55 - II. 平衡二叉树
思路:利用上一题求解二叉树的最大深度的方法,对于每一个节点,判断该节点的左右子树的最大高度差是否大于1
时间复杂度:最坏情况下为nlogn n为二叉树的结点数 对应满二叉树而言,每一层的节点数目是logn, 而每一层进行maxDepth的操作的时间复杂度是n
空间复杂度:O(n) 最坏情况下二叉树退化为链表
class Solution {
public boolean isBalanced(TreeNode root) {
if(root==null)
return true;
if(Math.abs(maxDepth(root.left)-maxDepth(root.right))>1)
return false;
return isBalanced(root.left)&&isBalanced(root.right);
}
public int maxDepth(TreeNode root) {
if(root==null)
return 0;
return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
}
}