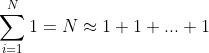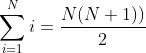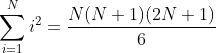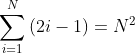1.代码时间复杂度
对于代码时间复制度的计算对于我其实一直都是“贝多芬”并没有真正掌握复杂度的计算。书写这篇博客的目的希望阅读本文后能清晰的知道自己代码的复杂度和一些优化技巧,并且希望读者将文章完善。
1.数学基础
数学对于数据结构的重要性好比航母起飞战斗机的初速度,只有初速度起来了才能飞得更远,但是代码中使用到的数学难度并没有那么大,所以静心学习便可掌握。
1.1等差数列
场景:比如确定到达边界值的次数
等差数列:
第n项: ![]()
前n项和证明:
![]()
![]()
两式相加得:
![]()
1.2等比数列
等比数列:
第n项: ![]()
前n项和证明:
![]()
![]()
两式相减得:
1.3指数
指数:
![]()
![]()
1.4对数
对数:
定义![]() ,当且仅当
,当且仅当![]()
则:
证明: ![]()
![]()
1.5级数
场景:代码循环或者递归结合最紧密的公式:
代码中常用的公式需要记住:
n个1的和
1.6小练习
证明 :
1.![]()
2.求精确时间
首先要明确代码是在计算机上运行的,代码的任何一个操作都会占用电脑运行时间。
public static int sum(int n){
int i , partialSum;
/*1*/ partialSum = 0; i = 0;
/*2*/ for( ;i < n; i++)
/*3*/ partialSum += i * i * i;
/*4*/ return partialSum;
}根据代码来推算出代码具体的运行时间,其中函数变量声明不计算时间。
1、第1行占2个单元时间;
2、第2行的i自增占2个单元时间(i自增和i 3、第3行每执行一次占用四个单元的时间(2个乘法运算1个加法运算和一次赋值)。套用等差数列公式:d=0,Sn=4n个单元时间; 4、第4行占1个单元时间; 因此,总的时间开销是6N+4。 通过计算代码运行的精确时间可以看出即使是计算几行简单代码的精确时间我们需要必须非常仔细和耗费大量的时间。那么对于更加复杂的代码求得精确时间不是更加困难? 影响电脑运行速度的因素非常多,而且数值n是趋近于无穷的。即使是计算出精确时间,但实际的运行时间肯定也会有明显差异,这样将很难评定代码的运行快慢。 相对增长率的概率便被提出。即忽视代码具体运行细节,通过相对增长率的大小来评定代码的运行快慢。映射到数学便是 函数求导,对比相同次数下函数的导数的大小来代码运行较快。 那么fn=6n+4 ,gn=n+100,但是他们增长率相同便认为代码好坏程度一样。都记为O(N)。大O符号表示法中,时间复杂度的公式是: T(n) = O( f(n) ),其中f(n) 表示每行代码执行次数之和,而 O 表示正比例关系,这个公式的全称是:算法的渐进时间复杂度。 下面列举一些常见的时间复杂度。 1.常数阶O(1) 无论代码执行了多少行,只要是没有循环等复杂结构,那这个代码的时间复杂度就都是O(1),如: 上述代码在执行的时候,它消耗的时候并不随着某个变量的增长而增长,那么无论这类代码有多长,即使有几万几十万行,都可以用O(1)来表示它的时间复杂度. 2.线性阶O(n) 代码从i=1开始,每次递增1,目标边界值为n,对应公式为: 3.对数阶O(logN) 代码从i=1开始, 每次为之前的2倍,目标边界值为n ,所以为 4.线性对数阶O(nlogN) 代码分为两层,分别对应公式为 5.平方阶O(n²) 代码分为两层,分别对应公式为 参考上面的O(n²) 去理解就好了,O(n³)相当于三层n循环,其它的类似。 其中相对增长率的大小有这个关系: 常数阶O(1) <对数阶O(logN)<线性阶O(n)<线性对数阶O(nlogN) <平方阶O(n²)<立方阶O(n³) 对应的增长曲线为: 要对程序进行优化,首先需要确定程序那部分可以优化。通过以上学习,其实优化的基本思路就是从高的相对增长率降低为较低的相对增长率。以下便是项目中常见的实战实例: 目前的时间复杂度为O(n²)。对代码分析后,可以看出第一个for1循环在对数据整体进行遍历,第二个for2循环则是在对条件进行查找。那么突破点便很明显了,for1是无法降低相对增长率的,但是查找有许多查找算法,只有选择相对增长率低于O(n)的即可。本文采用了二分查找的方法,复杂度为O(logN)。具体代码如下: 这样整体的算法复杂度是NlogN+N*logN,所以最后算法整体的复杂度为O(NlogN)。以此类推,可以优化O( 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现. 目前的时间复杂度为O(n²)。分析代码,复杂度较高的原因是寻找 给你一个链表的头节点 递归: 时间复杂度:O(n),其中 n 是链表的长度。递归过程中需要遍历链表一次。 空间复杂度:O(n),其中 n 是链表的长度。空间复杂度主要取决于递归调用栈,最多不会 超过 n 层。 链表: 时间复杂度:O(n),其中 n 是链表的长度。需要遍历链表一次。 空间复杂度:O(1)。 这里两种代码写法从数学层面的时间复杂度上是一样的,但是计算机实际运行时间其实还是有一定差距。这里体现了一种以空间换时间的思想,递归方式消耗的内存空间比链表形式消耗内存空间多,但是递归的运行时间会少于链表的运行时间。实战中需要根据项目的实际情况进行选择。 纸上得来终觉浅,绝知此事要躬行。通过本文虽然知道了如何计算时间复杂度和优化技巧,但是要熟练掌握还需要大量联系。附letcode,力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 (leetcode-cn.com). 3.运行时间基本思想
4.常见代码类型的运行时间
int i = 1;
int j = 2;
int m = i + j;for(i=1; i<=n; ++i)
{
j = i;
j++;
}![]() 。所以 for循环里面的代码会执行n遍,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用O(n)来表示它的时间复杂度。
。所以 for循环里面的代码会执行n遍,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用O(n)来表示它的时间复杂度。
int i = 1;
while(i![]() ,因此这类代码都可以用O(
,因此这类代码都可以用O(![]() )来表示它的时间复杂度。
)来表示它的时间复杂度。
for(m=1; m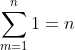 和
和![]() ,因此这类代码都可以用
,因此这类代码都可以用 ![]() (指数运算),但是按照一般法则取时间最大的函数,由下文得知
(指数运算),但是按照一般法则取时间最大的函数,由下文得知![]() 的相对增长率大于n,所以使用
的相对增长率大于n,所以使用![]() 来表示它的时间复杂度。
来表示它的时间复杂度。
for(x=1; i<=n; x++)
{
for(i=1; i<=n; i++)
{
j = i;
j++;
}
}
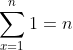 和
和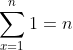 ,因此这类代码都可以用
,因此这类代码都可以用 ![]() 来表示它的时间复杂度。
来表示它的时间复杂度。![]() )
)5.优化实战
1.实例1-双重循环暴力求和
public int getCount(int[] arr) {
int count = 0;
int n = arr.length;
for (int i = 0; i < n; i++)
for (int j = i + 1; j < n; j++)
if (arr[i] == arr[j])
count++;
return count;
}public int getCount(int[] arr) {
int count = 0;
Arrays.sort(arr);
for (int i = 0; i < arr.length; i++)
if (Arrays.binarySearch(arr, arr[i]) > i)
count++;
return count;
}
![]() )等更高增长率的代码。
)等更高增长率的代码。 2.两数之和
public int[] twoSum(int[] nums, int target) {
int n = nums.length;
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
if (nums[i] + nums[j] == target) {
return new int[]{i, j};
}
}
}
return new int[0];
}
target - x 的时间复杂度过高。因此,我们需要一种更优秀的方法,能够快速寻找数组中是否存在目标元素。使用哈希表,可以将寻找 target - x 的时间复杂度降低到从 O(N) 降低到 O(1)。 public int[] twoSum(int[] nums, int target) {
Map 3.移除链表元素
head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。public ListNode removeElements(ListNode head, int val) {
if (head == null) {
return head;
}
head.next = removeElements(head.next, val);
return head.val == val ? head.next : head;
}public ListNode removeElements(ListNode head, int val) {
ListNode dummyHead = new ListNode(0);
dummyHead.next = head;
ListNode temp = dummyHead;
while (temp.next != null) {
if (temp.next.val == val) {
temp.next = temp.next.next;
} else {
temp = temp.next;
}
}
return dummyHead.next;
}
6.总结