归并排序 - 递归与非递归实现
目录
- 1. 归并排序
-
- 1.1 基本思想
- 1.2 代码实现
- 2. 非递归实现
-
- 2.1 边界易错点
- 2.2 代码实现
- 3. 特性总结
1. 归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。
1.1 基本思想
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并排序的总体结构是与快排十分相似类似于二叉树的结构,也是划分左右子区间分别递归进行排序,而与快排的区别在于:
- 快排是先排序,根据基准值划分子区间,再递归左右区间,当递归结束返回时数据就整体有序了。
- 归并排序则是先分割左右子区间,再进行递归,当递归返回时,借助于辅助数组进行归并排序,具体地:遍历两个区间,取小的尾插到辅助数组,最后再把辅助数组中已排好序的数据拷贝到原数组,结束后返回到上一层递归中继续对数据进行归并排序,并继续拷贝到原数组,当递归总体结束后,该数据的左右子区间都已有序,最后在把两边归并即可完成整体排序。
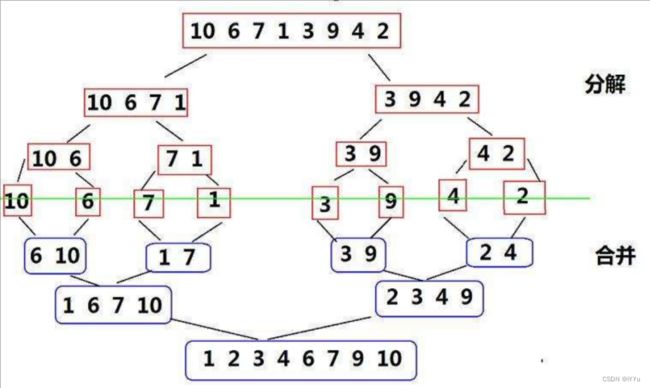
如上图,当递归到左右区间重叠也就是只有一个元素时(或者区间不存在),即可接停止递归开始归并。
这里会出现一个问题,必须借助额外数组吗?原数组交换位置行不行?
事实上交换位置无法正确排序,比如说这么一组数据,[3,4,5,6,1,2,3,4],左区间:[3,4,5,6] 右区间:[1,2,3,4],子区间都有序,此时如果是交换位置归并到原数组,即3和1交换位置后右区间为:[3,2,3,4],这时右区间就不再有序,所以必须要借助额外数组来进行归并。
还有一点需要注意:因为递归的区间不同,同样尾插到辅助数组中的起始位置也要不同,尾插到辅助数组的起始位置要与区间的起始位置保持一致,这样才能保证后面拷贝时不会把原数组中的数据给错误覆盖了。
1.2 代码实现
//[left,right]
void _MergeSort(int* a, int left, int right, int* tmp)
{
//当左右区间重合或者不存在即返回
if (left >= right)
{
return;
}
//取出中间位置
int mid = left + (right - left) / 2;
//划分左右子区间(左闭右闭)
//左子区间范围:
int begin1 = left, end1 = mid;
//右子区间范围:
int begin2 = mid + 1, end2 = right;
//分别递归两个区间
_MergeSort(a, begin1, end1, tmp);
_MergeSort(a, begin2, end2, tmp);
//到这个地方说明已经到了递归的最深处
//也就是最小规模的子问题
//即左右子区间就各有一个值
//开始归并
//注意:tmp下标i要与区间的起始位置left保持一致
int i = left;
//依次遍历两个区间取小的尾插到辅助数组中
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
//因为是轮流走,因此一定会有一个先结束
//不管谁先结束,直接把没结束的哪个区间的数据依次插入
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
//这两个循环一定只有一个会进入
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//最后把tmp中有序的区间数据拷贝回原数组
memcpy(a + left, tmp + left, (right - left + 1) * 4);
}
// 归并排序递归实现
void MergeSort(int* a, int n)
{
//开辟辅助数组
int* tmp = (int*)malloc(sizeof(int) * n);
assert(tmp);
//归并排序主逻辑实现
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
}
2. 非递归实现
相较于递归而言,非递归是比较难的,而且各种边界判断也比较麻烦,接下来一点点分析。
基本思路:根据递归的结构不难看出,归并排序的本质也是分割区间分别进行处理,并且归并前要求两个区间范围要分别有序,因此第一步是通过迭代来控制边界到达最小的区间也就是两个区间重叠的位置开始归并,然后不断扩大区间继续归并。
先定义gap初始化为1来帮助控制最小范围右区间边界:
//{ 7,6,5,4,3,2,1,0 };
int gap = 1;
for (int j = 0; j < n; j += gap * 2)
{
//左区间起始和结束位置
//闭区间需要-1
int left1 = j, righ1 = j + gap - 1;
//右区间起始和结束位置
int left2 = j = gap, righ2 = j + 2 * gap - 1;
printf("[%d][%d] - [%d][%d]\n\n", left1, righ1, left2, righ2);
}
当前循环j一次会走2*gap个距离,也就是一次走两步,因此每次都会刚好会分割出两个最小的子区间:

此时开始归并,一一归并结束后,拷贝回原数组,增加gap*2开始两两归并,然后继续gap*2,四四归并,由于当前数据是8个当四四归并结束后整体就结束了。
代码实现:
// 归并排序非递归实现
//{ 7,6,5,4,3,2,1,0 };
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (!tmp)
{
return;
}
//首先gap为1
int gap = 1;
while (gap < n)
{
for (int j = 0; j < n; j += gap * 2)
{
//左区间起始和结束位置
//闭区间需要-1
int begin1 = j, end1 = j + gap - 1;
//右区间起始和结束位置
int begin2 = j + gap, end2 = j + 2 * gap - 1;
printf("[%d %d] [%d %d] ", begin1, end1, begin2, end2);
//归并逻辑与递归相同
int i = j;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//这次选择归一次拷一次
memcpy(a + j, tmp + j, 4 * (end2 - j + 1));
}
//然后增加gap为原来的二倍扩大区间范围继续合并
gap *= 2;
printf("\n");
}
free(tmp);
}
2.1 边界易错点
如果是奇数个呢?此时增加一个数据a = { 8,7,6,5,4,3,2,1,0 };来看上面的代码是否可以正确执行:

这里程序已经挂掉了,上图可以发现有些区间已经越界了:

这是奇数的情况,那么是偶数但不是2的指数个的情况,数据有没有问题?再给a增加一个数据到10个:a = { 9,8,7,6,5,4,3,2,1,0 };

上图可以看出,虽然是偶数,但不是2的指数个数据的情况也会存在越界,且与奇数个的大部分情况相同。
这两个情况的越界都可以分为三种:
- end1就已经越界了
- begin2和end2整体越界
- end2部分越界
分别分析这三种情况:
- 当end1就已经越界了,说明右区间不存在,不存在就自然没法进行归并了,所以这种情况之间跳出循环。
- 当begin2越界和end2整体越界,也同样说明右区间不存在,不存在就没法与左区间归并。因此也跳出循环。
- end2越界,说明右区间存在,但是end2位置不存在,既然有存在的那必然需要进行归并,但是归并的范围不可以到end2而是到n-1,所以只需要把右区间的范围从end2缩小到n-1即可。
这三种边界情况处理好后就没什么问题了。
2.2 代码实现
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (!tmp)
{
return;
}
//首先gap为1
int gap = 1;
while (gap < n)
{
for (int j = 0; j < n; j += gap * 2)
{
//左区间起始和结束位置
//闭区间需要-1
int begin1 = j, end1 = j + gap - 1;
//右区间起始和结束位置
int begin2 = j + gap, end2 = j + 2 * gap - 1;
//归并逻辑与递归相同
//判断三种边界情况
if (end1 >= n || begin2 >= n)
{
break;
}
else if (end2 >= n)
{
end2 = n - 1;
}
int i = j;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//这次选择归一次拷一次
memcpy(a + j, tmp + j, 4 * (end2 - j + 1));
}
//然后增加gap为原来的二倍扩大区间范围继续合并
gap *= 2;
printf("\n");
}
free(tmp);
}
以上就是归并排序的总体思路及代码实现,非递归需要对边界的处理更加仔细。
3. 特性总结
归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定

