2021-ACS-IGN: A Novel and Efficient Deep Graph Representation Learning Framework for Accurate

2021-ACS-IGN: A Novel and Efficient Deep Graph Representation Learning Framework for Accurate

Paper: http://pubs.acs.org/doi/10.1021/acs.jmedchem.1c01830

Code: https://github.com/zjujdj/InteractionGraphNet/tree/master

InteractionGraphNet：一种新颖高效的深度图表示学习框架，用于准确的蛋白质-配体相互作用预测

本文由浙江大学智能创新药物研究院侯廷军教授团队, 浙江大学计算机学院吴健教授团队,中南大学曹东升团队和腾讯量子实验室联合在药物化学领域权威期刊 Journal of Medicinal Chemistry发表的一篇文章。改文章提出了一个名为InteractionGraphNet（IGN）的新型深度图表示学习框架，用于从蛋白质 - 配体复合物的3D结构中学习蛋白质 - 配体相互作用。在IGN中，堆叠了两个独立的图卷积模块，以顺序学习分子内和分子间的相互作用，并且学习到的分子间相互作用应用于下游的任务预测, 包括结合亲和力预测、大规模基于结构的虚拟筛选和姿态预测，实验表明，与其他最先进的基于 ML 的基线和对接程序相比，IGN 取得了更好或更具竞争力的性能。

数据集

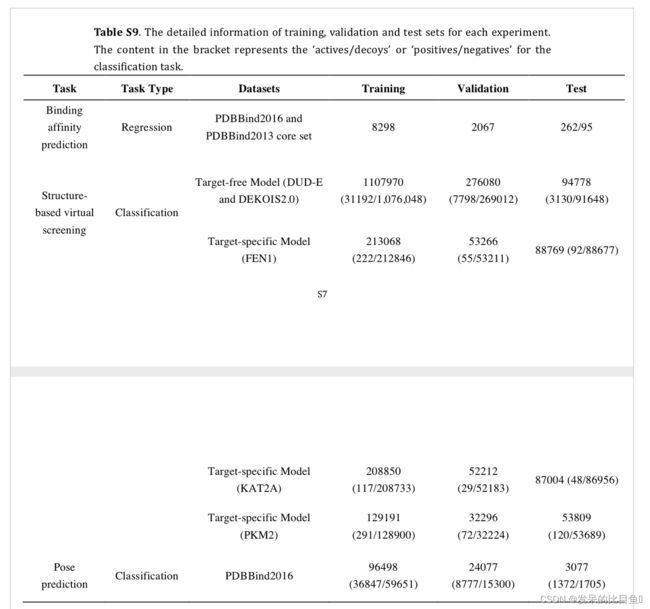
四个数据集，包括PDBBind V2016（2016版），DUD-E, DEKOIS2.0 和LIT-PCBA

模型

IGN模型的详细框架，该模型主要包括五个模块：图表示模块，分子内图卷积模块，分子间图卷积模块，图池模块和任务网络模块（图1）。

嵌入化学和 3D 结构信息的图形表示

该模块总共使用三个分子图来编码蛋白质-配体复合物的分子内相互作用和分子间相互作用，即配体图$(G_l=(V_l,E_l))$，蛋白质图$(G_p=(V_p,E_p))$和蛋白质-配体图$(Gpl=(V_{pl}，E_{pl}))$。相应的邻接矩阵 $A_{ij}^l$、$A_{ij}^p$ 和 $A_{ij}^{pl}$ 定义如下：
$A_{ij}^1=\{\begin{array}{l}1,\text{ if }i,j\in \text{ ligand atoms and }i,j\text{ are connected }\\ 0,\text{ otherwise }\end{array}$

$A_{ij}^{\mathrm{p}}=\{\begin{array}{l}1,\text{ if }i,j\in \text{ protein atoms and }i,j\text{ are connected }\\ 0,\text{ otherwise }\end{array}$

$A_{ij}^{\mathrm{pl}}=\{\begin{array}{l}1,\text{ if }i\in \text{ ligand atoms and }j\in \text{ protein atoms and }{d}_{ij}\\ <8\mathring{A}\\ 1,\text{ if }j\in \text{ protein atoms and }i\in \text{ ligand atoms and }{d}_{ij}\\ <8\mathring{A}\\ 0,\text{ otherwise }\end{array}$

其中$G_{pl}=(V_{pl}，E_{pl})$是一个二分图，它的每一个边缘连接蛋白质中的一个原子和配体中的另一个原子。二分图在生物分子中的成功应用已有报道。$d_{ij}$是两个原子之间的欧几里得距离，这样的定义假设两个蛋白质配体成对原子之间的某些相互作用存在于$G_{pl}$中的阈值$d_{ij}$内。在这里，$d_{ij}$ 设置为结合亲和力预测任务的 $8\mathring{A}$，以及大规模 SBVS 和位姿预测任务的 $5\mathring{A}$。该阈值是经验性的和可优化的，其他一些阈值（例如 $3$ 和 $12\mathring{A}$）也进行了简单的测试。但是，综合考虑精度和可计算性，$8\mathring{A}$的选择总体上是不错的。配体或蛋白质中的分子内相互作用由原子之间的共价键表示，并且为了计算效率的目的，不考虑配体或蛋白质中的非键合原子。所有配合物均经过预处理，得到具有节点特征和边缘特征的相应分子图。对于 $G_l$ 和 $G_p$，它们共享支持信息表 S7 中描述的一组 2D 节点描述和 2D 边缘描述。


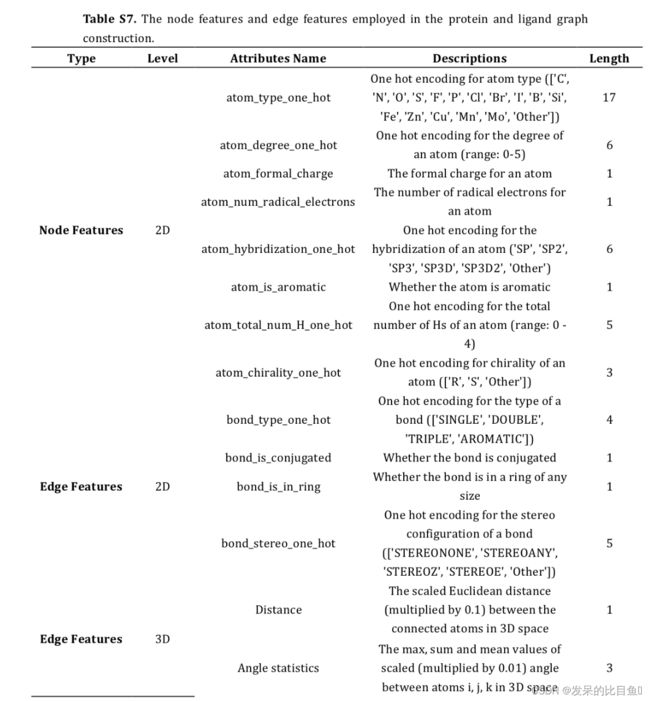
由于蛋白质-配体相互作用受到3D空间中原子之间的空间距离和方向的严格控制，因此设计了另一组与3D结构相关的几何特征，包括距离，角度统计，面积统计和距离统计，作为$G_l$和$G_p$的外边特征。这些特征是基于原子的空间坐标计算的，它们对于蛋白质-配体复合物的旋转和平移是不变的，其中旋转和平移不变性在3DCNN表示的一些评分函数中通常缺失。该算法的伪代码和公式显示在支持信息表 S8 中。对于 $G_{PL}$，初始节点特征直接继承自分子内图卷积模块（图 1），边缘特征仅包括两个连接原子的直观欧几里得距离。

分子内图卷积模块。本模块旨在学习$G_l$和$G_p$的节点表示，这些表示主要由连接的原子和键的化学环境决定。本模块的学习过程包含三个步骤：

• 步骤1：获取节点的初始表示;
• 步骤2：通过消息传递的K次迭代更新节点的表示形式;
• 步骤3：提取 $G_l$ 和 $G_p$ 节点的最终表示。

本模块中使用的一般符号如下：$a_i$表示原子$i$的初始原子特征，维度为F1; $b_{ij}$表示绑定 $ij$的初始绑定特征，维度为 F2，下标 $ij$ 表示从节点 $i$ 发送到节点 $j$（即从源节点到目标节点）的消息;$hit$ 是节点 $i$ 在时间步 $t$ 处的表示;$N(i)$ 表示节点 $i$ 的相邻节点;$D$ 是节点隐藏状态的维度;$D^{{}^{\prime }}$ 是门控循环单元 （GRU） 的输入大小;$||$是串联操作;LeakyReLU、ELU 和 ReLU 是非线性激活;BN 是批处理规范化操作。

本模块的三个步骤的详细信息如下：
第 1 步：获取节点的初始表示

a i new  = LeakyReLU ⁡ ( w 1 a i ) , w 1 ∈ R D × F 1 b i j new  = LeakyReLU ⁡ ( w 2 [ a i ∥ b i j ] ) , w 2 ∈ R D × ( F 1 + F 2 ) s i j = LeakyReLU ⁡ ( w 3 [ a j new  ∥ b i j new  ] ) , w 3 ∈ R 1 × 2 D α i j = exp ⁡ ( s i j ) ∑ k ε N ( i ) exp ⁡ ( s i k ) m i = ELU ⁡ ( ∑ k ε N ( i ) α i k w 4 b i k new  ) , w 4 ∈ R D ′ × D h i 0 = ReLU ⁡ ( GRU ⁡ ( m i , a i new  ) ) \begin{aligned} & a_i^{\text {new }}=\operatorname{LeakyReLU}\left(w_1 a_i\right), \quad w_1 \in \mathbb{R}^{D \times F 1} \\ & b_{i j}^{\text {new }}=\operatorname{LeakyReLU}\left(w_2\left[a_i \| b_{i j}\right]\right), \quad w_2 \in \mathbb{R}^{D \times(F 1+F 2)} \\ & s_{i j}=\operatorname{LeakyReLU}\left(w_3\left[a_j^{\text {new }} \| b_{i j}^{\text {new }}\right]\right), \quad w_3 \in \mathbb{R}^{1 \times 2 D} \\ & \alpha_{i j}=\frac{\exp \left(s_{i j}\right)}{\sum_{k \varepsilon N_{(i)}} \exp \left(s_{i k}\right)} \\ & m_i=\operatorname{ELU}\left(\sum_{k \varepsilon N_{(i)}} \alpha_{i k} w_4 b_{i k}^{\text {new }}\right), \quad w_4 \in \mathbb{R}^{D^{\prime} \times D} \\ & h_i^0=\operatorname{ReLU}\left(\operatorname{GRU}\left(m_i, a_i^{\text {new }}\right)\right) \end{aligned} ​ainew ​=LeakyReLU(w1​ai​),w1​∈RD×F1bijnew ​=LeakyReLU(w2​[ai​∥bij​]),w2​∈RD×(F1+F2)sij​=LeakyReLU(w3​[ajnew ​∥bijnew ​]),w3​∈R1×2Dαij​=∑kεN(i)​​exp(sik​)exp(sij​)​mi​=ELU ​kεN(i)​∑​αik​w4​biknew ​ ​,w4​∈RD′×Dhi0​=ReLU(GRU(mi​,ainew ​))​

其中 $a_i^{new}$ 和 $b_{ij}^{new}$ 由初始原子特征 $a_i$ 和键特征 $b_{ij}$ 的线性变换生成，然后根据 eqs 4 和 5 进行非线性激活。然后，通过方程6计算两个连接的原子$i$和$j$之间的非规范化注意力得分$s_{ij}$。方程7中的softmax函数用于归一化每个原子连接键上的注意力得分。接下来，使用方程 8 中定义的消息函数来计算 atom i 的加权传入消息 $m_i$。最后，使用GRU和非线性激活作为原子更新函数，将变换后的初始原子特征$a_i^{new}$融合并接受消息$m_i$到atom $i$: $h_i^0$的初始表示中。

步骤 2：通过消息传递的 $k$ 次迭代更新节点的初始表示

s i j l = LeakyReLU ⁡ ( w 1 l [ h i l − 1 ∥ h j l − 1 ] ) , w 1 l ∈ R 1 × 2 D α i j l = exp ⁡ ( s i j l ) ∑ k ε N ( i ) exp ⁡ ( s i k l ) m i l = ELU ⁡ ( ∑ k ε N ( i ) α i k l w 2 l h k l − 1 ) , w 2 l ∈ R D ′ × D h i l = ReLU ⁡ ( GRU ⁡ ( m i l , h i l − 1 ) ) h i l = BN ⁡ ( h i l ) \begin{aligned} s_{i j}^l & =\operatorname{LeakyReLU}\left(w_1^l\left[h_i^{l-1} \| h_j^{l-1}\right]\right), \quad w_1^l \in \mathbb{R}^{1 \times 2 D} \\ \alpha_{i j}^l & =\frac{\exp \left(s_{i j}^l\right)}{\sum_{k \varepsilon N_{(i)}} \exp \left(s_{i k}^l\right)} \\ m_i^l & =\operatorname{ELU}\left(\sum_{k \varepsilon N_{(i)}} \alpha_{i k}^l w_2^l h_k^{l-1}\right), \quad w_2^l \in \mathbb{R}^{D^{\prime} \times D} \\ h_i^l & =\operatorname{ReLU}\left(\operatorname{GRU}\left(m_i^l, h_i^{l-1}\right)\right) \\ h_i^l & =\operatorname{BN}\left(h_i^l\right) \end{aligned} sijl​αijl​mil​hil​hil​​=LeakyReLU(w1l​[hil−1​∥hjl−1​]),w1l​∈R1×2D=∑kεN(i)​​exp(sikl​)exp(sijl​)​=ELU ​kεN(i)​∑​αikl​w2l​hkl−1​ ​,w2l​∈RD′×D=ReLU(GRU(mil​,hil−1​))=BN(hil​)​

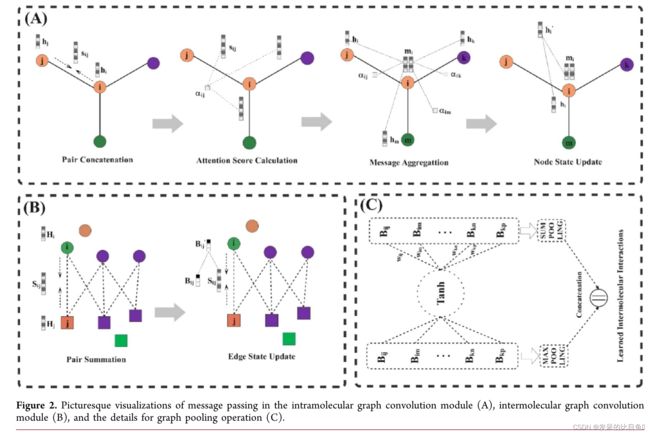
该模块使用的消息传递主要包含四个阶段：对连接、注意力分数计算、消息聚合和原子隐藏状态更新（图 2A）。
步骤 3：获取最终节点表示
$h_i^{t+1}={\sum }_{t=1}^k{h}_i^t$
使用最后一个隐藏层中的节点表示进行后续任务的研究不同，作者采用了混合节点表示聚合，通过跳过连接将每个隐藏层中的节点表示聚合到最终节点表示中，这种混合聚合方式可以缓解聚合半径增大带来的过平滑问题，同时提高节点的多样性。

分子间图卷积模块

由于配合物中的分子间相互作用主要由蛋白质原子和配体原子之间的非共价/非键相互作用决定，因此该模块旨在学习有效描述$G_{pl}$中蛋白质原子和配体原子之间成对原子相互作用的边缘表示（图2B）。同样，此模块中使用的通用符号列出如下：$B_{ij}$表示 $G_{pl}$中边 $ij$的初始边特征;$H_i$表示 $G_{pl}$中节点 $i$的初始原子特征。
$\begin{array}{rl}& H_i=h_i^{t+1}\\ & B_{ij}^{\text{new }}=\mathrm{MLP}\left(\left[B_{ij}\Vert \left(H_i+H_j\right)\right]\right)\\ & B_{ij}^{\text{new }}=\mathrm{BN}\left(B_{ij}^{\text{new }}\right)\end{array}$
其中 $G_{pl}$ 中节点 $i$的初始特征直接继承自 $G_l$和 $G_p$中相应的最终节点表示，该表示根据方程 16 在 3D 空间中编码共价化学环境。$G_{pl}$中新增的边表示 ，其中两个连接原子的初始原子特征和初始边缘特征之和的串联被馈送到多层感知器 （MLP） 中以产生表示，并且这样的设计逻辑旨在强制边缘 $ij$和 $ji$共享相同的表示。同样，批量规范化操作用于加速深度网络的训练。

图形池化模块

图池旨在提取分子图的全局表达式。在蛋白质-配体识别的基本物理原理的驱动下，图池模块仅适用于Bnew，可以将其视为学习成对原子非键相互作用以产生复合物的分子间相互作用（图2C）。

其中具体的函数形式由模型自动学习。本模块中使用的一般符号如下：$tanh$ 是非线性激活;$E_{pl}$是 $G_{pl}$ 中的边集;$D^{\prime \prime }$， MLP 的输出维度;MAXPOOl 是边特征所有值的元素最大值。
$\begin{array}{rl}& G_1^{\ast }=\sum \tanh \left(w_1^{\ast }{B}_{ij}^{\mathrm{new}}\right)\ast B_{ij}^{\mathrm{new}},\forall ij\in E_{\mathrm{p}1},w_1^{\ast }\in {\mathbb{R}}^{1\times D^{\prime \prime }}\\ & B^{\mathrm{new}}=B_{ij}^{\mathrm{new}},\forall ij\in E_{\mathrm{pl}}\\ & G_2^{\ast }=\mathrm{MAXPOOl}\left(B^{\mathrm{new}}\right)\\ & G^{\ast }=\left[G_1^{\ast }\Vert G_2^{\ast }\right]\end{array}$
其中图形池化 $G^{\ast }$ 的输出由加权和池化 $G_1^{\ast }$ 和最大池化 $G_2^{\ast }$ 组合而成。这种考虑可以利用多视图的信息，其中最大池化可以突出显示信息强度最高的边要素，加权和池化可以利用边要素的总信息强度。

任务层模块

批量归一化层增强的FCNN被用作最终蛋白质-配体相互作用预测的任务网络，因为它能够成为任何非线性函数的通用逼近器。训练目标是最小化损失函数。给定一个包含 N 个样本的数据集，某个样本的预测值和真实值分别为 ${\hat{y}}_i$和 $y_i$。结合亲和力预测任务（回归任务）的损失函数（MSE损失），SBVS和姿势预测任务（分类任务）的损失函数
$\begin{array}{rl}& \text{ MSE loss }=\frac{1}{N}\sum _{i=1}^N{\left(y_i-\widehat{y_i}\right)}^2\\ & \text{ focal loss }=-\frac{1}{N}\sum _{i=1}^N\alpha (1-\mathrm{sigmoid}(\hat{y}){)}^{\gamma }\log (\mathrm{sigmoid}(\hat{y}))\end{array}$

模型训练

评价指标

• 采用RMSE和皮尔逊相关系数（Rp）等2个主要指标对回归模型（结合亲和力预测任务）质量进行评价。
• 对于SBVS任务，五个指标包括AUC_ROC，AUC_PRC，LogAUC，BEDROC（本研究中α = 80.5）和不同阈值（0.1，0.5，1和5%）的EF。
• 对于姿势预测任务，考三个指标，即AUC_ROC、AUC_PRC和top1成功率。