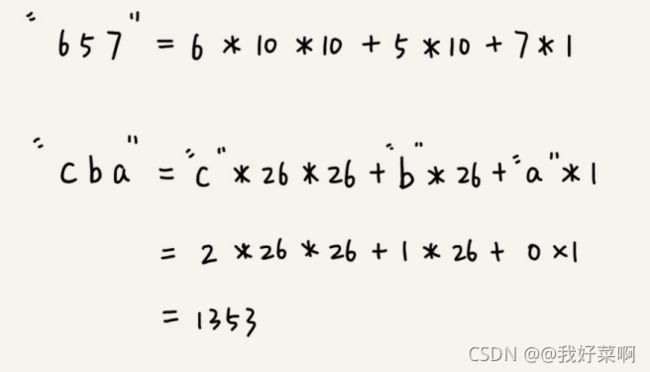一看就懂的字符串匹配算法 之 RK算法
RK算法是对BF算法的进一步优化,很巧妙的使用了哈希算法,让匹配的效率有了很大的提升。
BF算法 这是关于BF暴力匹配算法的博客,大家可以先去看看。
RK算法的原理和实现
之前在讨论BF算法的时候,我们说过关于模式串长度m,和主串长度n,那么在主串中就会有n-m+1个长度为m的子串,我们只需要暴力的一一对比n-m+1个子串与模式串,就可以找出主串中与模式串匹配的子串。
但是这样就会出现一个问题,在每次检查子串和模式串是否匹配的时候,需要依次对比每个字符,比较耗时,所以我们现在就需要稍微进行改造,增加哈希算法,来加快子串与模式串的匹配。
具体的思路是通过哈希算法对主串中的n-m+1个子串分别求哈希值,然后与模式串的哈希值进行比较。如果某个子串的哈希值等于模式串,那就说明子串与模式串相匹配(暂时不讨论哈希冲突的问题)。因为哈希值是一个数字,数字之间比较是否相等是非常快速的,所以模式串和子串的比对的效率就提高了。
这时候大家可能也注意到一个问题了,就是尽管借助了哈希值,模式串与子串比对的效率提高了,不过通过哈希算法计算子串哈希值的过程,需要遍历子串中的每个字符,这个过程就比较耗时。也就是说,整体的效率并没有提高。
那我们如果假设主串和模式串对应的字符集只包含K个字符,我们可以用一个K进制数来表示一个子串,把K进制数转换为十进制数,作为子串的哈希值。现在看看这个例子。
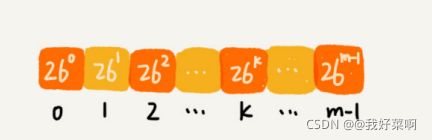
例如:要处理的字符串只包含a到z这26个小写字母,那么我们就用26进制来表示一个子串,我们把a到z这26个字符映射到0到25这26个数字,如下图一样,计算哈希值时,相对于十进制字符串,我们只需要把进位从10改为26.
上面说的哈希算法有一个特点:在主串中,相邻两个子串哈希值的计算公式有一顶的关系。
上图这是十进制字符串和十六进制字符串的哈希值计算。
上图是相邻子串哈希值计算。
通过这个例子,我们可以得出这样的规律:相邻子串s[i-1]和s[i]对应的哈希值计算公式有交集,也就是说,我们可以使用s[i-1]的哈希值快速的计算出s[i]的哈希值。
RK算法的性能分析
RK算法耗时的逻辑主要包含两个部分:计算子串的哈希值和比较模式串与子串的哈希值。对于计算字串的哈希值,我们可以设计特殊的哈希算法,只需要扫描一遍主串就能得到所以子串的哈希值,因此,这一部分的时间复杂度为O(n)。对于比较模式串与子串的哈希值,这部分的时间复杂度也为O(n)。综合起来,RK算法的时间复杂度为O(n)。
这个时候可能还会出现一个问题,图个模式串很长,相对应的主串中的子串也很长,那么通过上面计算出的哈希值可能就会很大,如果哈希值超过了计算机整型类型可以表示的范围,那又应该怎么办呢?
实际上,前面设计的基于二十六进制的哈希算法是没有哈希冲突的,也就是说,一个字符串与一个二十六进制数一一对应,不同的字符串的哈希值肯定不一样,十六进制字符串对应的十进制也是不会有冲突的。不过,对于模式串很长的情况下,为了能将哈希值落在整形数据表示的范围内,存在哈希冲突也是可以接收的,那么此时又该怎么设计哈希算法呢?
基于C语言的代码
//
// main.c
// 003--RK匹配算法
//
// Created by CC老师 on 2019/10/29.
// Copyright © 2019年 CC老师. All rights reserved.
//
#include
#include
#include
//d 表示进制
#define d 26
//4.为了杜绝哈希冲突. 当前发现模式串和子串的HashValue 是一样的时候.还是需要二次确认2个字符串是否相等.
int isMatch(char *S, int i, char *P, int m)
{
int is, ip;
for(is=i, ip=0; is != m && ip != m; is++, ip++)
if(S[is] != P[ip])
return 0;
return 1;
}
//3.算出最d进制下的最高位
//d^(m-1)位的值;
int getMaxValue(int m){
int h = 1;
for(int i = 0;i < m - 1;i++){
h = (h*d);
}
return h;
}
/*
* 字符串匹配的RK算法
* Author:Rabin & Karp
* 若成功匹配返回主串中的偏移,否则返回-1
*/
int RK(char *S, char *P)
{
//1. n:主串长度, m:子串长度
int m = (int) strlen(P);
int n = (int) strlen(S);
printf("主串长度为:%d,子串长度为:%d\n",n,m);
//A.模式串的哈希值; St.主串分解子串的哈希值;
unsigned int A = 0;
unsigned int St = 0;
//2.求得子串与主串中0~m字符串的哈希值[计算子串与主串0-m的哈希值]
//循环[0,m)获取模式串A的HashValue以及主串第一个[0,m)的HashValue
//此时主串:"abcaadddabceeffccdd" 它的[0,2)是ab
//此时模式串:"cc"
//cc = 2 * 26^1 + 2 *26 ^0 = 52+2 = 54;
//ab = 0 * 26^1 + 1 *26^0 = 0+1 = 1;
for(int i = 0; i != m; i++){
//第一次 A = 0*26+2;
//第二次 A = 2*26+2;
A = (d*A + (P[i] - 'a'));
//第一次 st = 0*26+0
//第二次 st = 0*26+1
St = (d*St + (S[i] - 'a'));
}
//3. 获取d^m-1值(因为经常要用d^m-1进制值)
int hValue = getMaxValue(m);
//4.遍历[0,n-m], 判断模式串HashValue A是否和其他子串的HashValue 一致.
//不一致则继续求得下一个HashValue
//如果一致则进行二次确认判断,2个字符串是否真正相等.反正哈希值冲突导致错误
//注意细节:
//① 在进入循环时,就已经得到子串的哈希值以及主串的[0,m)的哈希值,可以直接进行第一轮比较;
//② 哈希值相等后,再次用字符串进行比较.防止哈希值冲突;
//③ 如果不相等,利用在循环之前已经计算好的st[0] 来计算后面的st[1];
//④ 在对比过程,并不是一次性把所有的主串子串都求解好Hash值. 而是是借助s[i]来求解s[i+1] . 简单说就是一边比较哈希值,一边计算哈希值;
for(int i = 0; i <= n-m; i++){
if(A == St)
if(isMatch(S,i,P,m))
return i;
St = ((St - hValue*(S[i]-'a'))*d + (S[i+m]-'a'));
}
return -1;
}
int main()
{
char *buf="abcaadddabceeffccdd";
char *ptrn="cc";
printf("主串为%s\n",buf);
printf("子串为%s\n",ptrn);
int index = RK(buf, ptrn);
printf("find index : %d\n",index);
return 1;
}